Area Between A Function And Its Inverse
Find the area bounded by the curve f ( x ) = x + sin ( x ) and its inverse function between the values x = 0 and x = 2 π .
The answer is 8.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Brian, your solution makes the error / assumption that a function and it's inverse can only intersect on the line y = x , which is not necessarily true.
You're lucky because in this case, the function is non-decreasing, and hence it can be shown that any intersection point lies on the line y = x .
Log in to reply
Fair enough. Since f ′ ( x ) = cos ( x ) + 1 ≥ 0 we know that f ( x ) is non-decreasing. Also, if g ( x ) is the inverse, then g ′ ( x ) = f ′ ( g ( x ) ) 1 wherever the derivative of f is non-zero, and so g ( x ) is non-decreasing as well. Furthermore, we see that f ( x ) = x for x = n π for any integer n , and that f ′ ( x ) is never 1 at these intersection points. Thus each time f ( x ) intersects y = x it in fact crosses this line fully. Is this enough information to justify the assumptions in my solution?
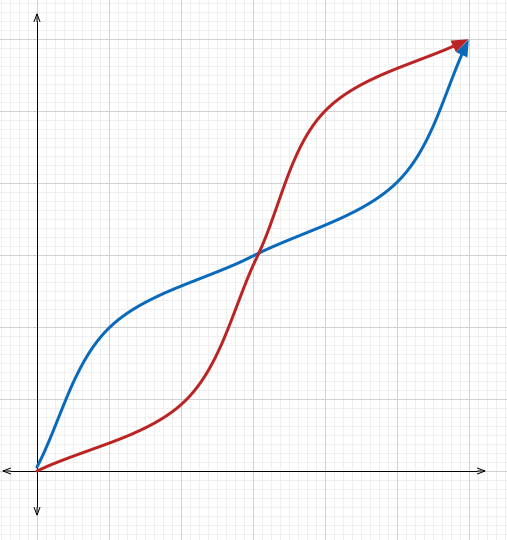
P.S.. Looking at your diagram, I would have though the blue line would be horizontal at x = n π and the red line vertical at these points of intersection. That said, my feeling is that while a diagram normally enhances a posting, in this case a diagram would give away too much and thus detract from its worth.
Log in to reply
There is a simpler solution. Suppose that ( x , y ) is a point of intersection of these graphs with x = y . Then, the point ( y , x ) is also a point of intersection of these graphs. Hence, the points ( x , y ) , ( y , x ) are points that lie on the graph y = f ( x ) . By the mean value theorem , there must be a point c such that f ′ ( c ) = x − y y − x = − 1 , which contradicts the assumption that f is increasing. In fact, this also shows that if f ′ ( x ) > − 1 , then the only points of intersection are of the form ( x , x ) .
Agreed on the diagram giving away too much, which is why I was hesitant to add it to the problem. I shall not add it on.
Log in to reply
@Calvin Lin – Ah, o.k., that's a great solution. Thanks. :)
@Calvin Lin – Sir, I think you should not add the graph due to the simple reason that sketching the graph is also a part of the problem. @Calvin Lin
Sir, why is it wrong to say that a function and it's inverse always intersects on the line y=x? I always thought it did. Thanks.
Log in to reply
The key word is only .
For example, if you consider the function f ( x ) = x 1 , and the inverse function f − 1 ( x ) = x 1 , then you will see that the intersection of these 2 graphs is exactly y = x 1 . In particular, they intersect at points which do not satisfy y = x .
@Sandeep Bhardwaj I am tempted to add the following image to the problem, but I am concerned that it could give away too much. What are your thoughts?
Great solution....I was confused in drawing it's graph ..can you tell me how to draw graph of such functions...and also please tell how to find out period of any give complex trigonometric function.. Thnkx
In above figure the shaded region is the required area.
in the figure we can sea that the total required area is equal to 4x(area of the gray region)
and the area of the gray region = ∫ 0 π x + s i n x − 1 / 2 ∗ π 2 = 2
hence total required area = 4 × 2 = 8
Best method
to find the intended area, we only have to find the area between y = x + sin x and y = x for x ∈ [ 0 , 2 π ] and then multiply the result by 2
now your task is to find the intersection between y = x + sin x and y = x and separate the integral!
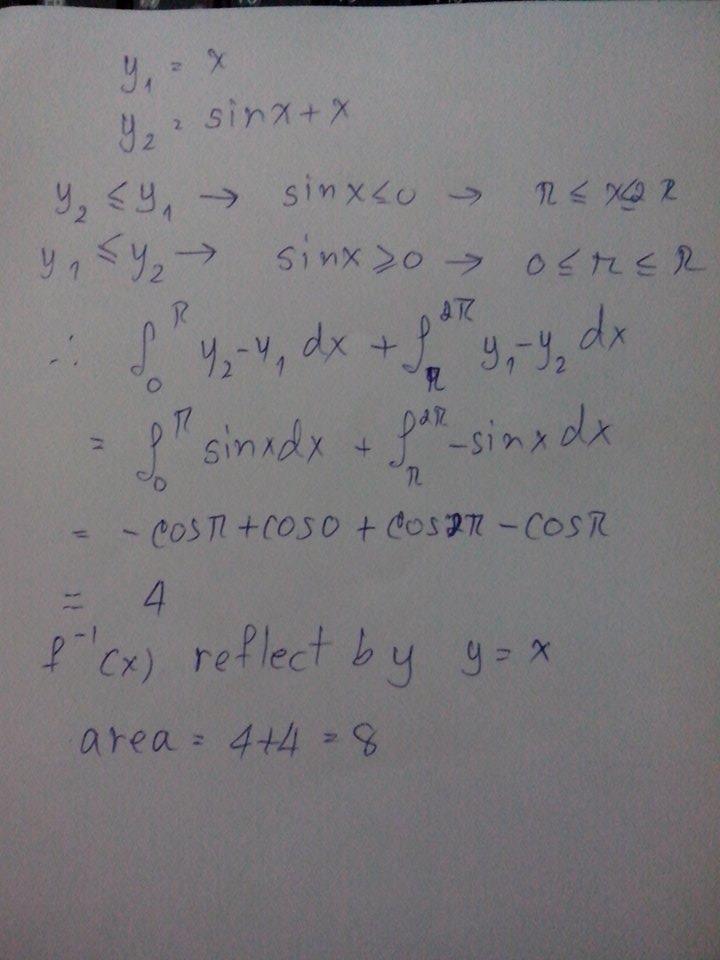
The actual inverse of the given function can't be phrased in terms of standard functions, so we'll have to take a more intuitive approach. Note that the inverse of a function is its reflection about the line y = x . Now in relation to this axis of reflection, the given function is periodic with period 2 π . So if we calculate the area bounded by the given function and the line y = x from x = 0 to x = π and then multiply this result by 4 we will find the desired area. This will then be
4 ∗ ∫ 0 π ( f ( x ) − x ) d x = 4 ∗ ∫ 0 π sin ( x ) d x = − 4 cos ( x )
evaluated from x = 0 to x = π , which comes out to − 4 ∗ ( − 2 ) = 8 .