Box inside Box

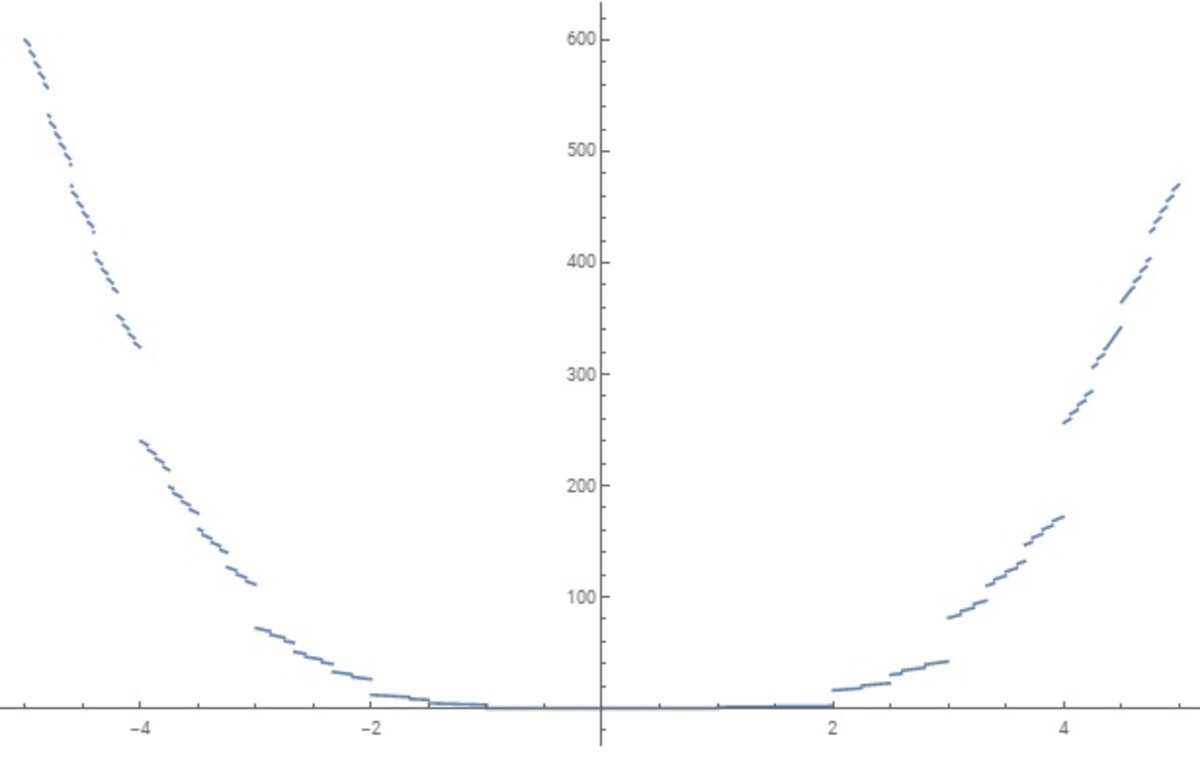
First note that $x$ can't be an integer. Now note that $\lfloor x \cdot \lfloor x \cdot \lfloor x \rfloor \rfloor \rfloor$ is an integer, say $n$ , so $x=\frac{88}{n}$

It's easy to see that $f(x)=x \cdot \lfloor x \cdot \lfloor x \cdot \lfloor x \rfloor \rfloor \rfloor$ is an increasing function*, and that $f(3)=81$ and $f(4)=256$ , so $3<x<4$ and $22<n\le 29$ .

This only leaves eight possible $n$ to check; just one value, $n=28$ , works, so $x=\frac{88}{28}=\frac{22}{7}$ and the answer is $\boxed{29}$ .

Incidentally, $f(\pi)=87.96\ldots$ .

---

• As Mark Hennings points out, $f$ is only increasing for positive $x$ ; but there are no solutions for negative $x$ (see the comments below).