Box on Two Surfaces (Part 2)
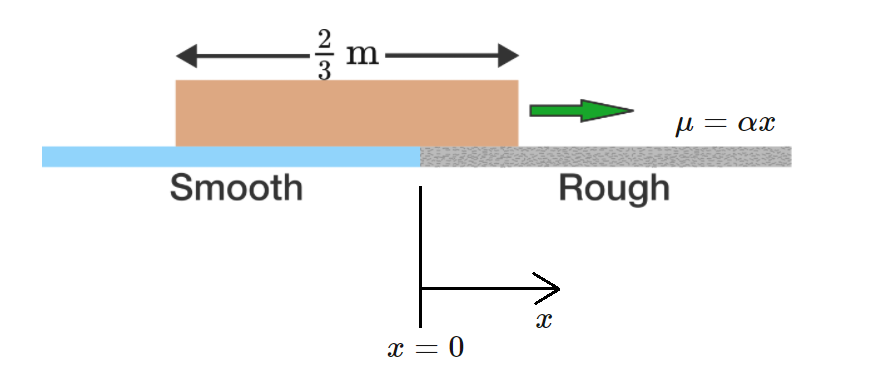
A rectangular box of length 3 2 m is initially traveling at 2 m/s , with its entire length over the smooth (perfectly frictionless) blue surface (shown above). The box gradually moves onto a rough surface (gray) and stops the instant that its entire length is positioned within the rough region.
Call the distance into the rough region x . The coefficient of friction varies within the rough region according to ( μ = α x ).
Determine the value of α .
Details and Assumptions:
- g = 1 0 m/s 2 .
- The pressure at the bottom of the box is always uniform over its area.
- Note that the friction coefficient is non-uniform over space. But at any point in space, the friction coefficient is uniform over time.
The answer is 2.7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Ah. Lovely question :)... What would it be .. if μ = k v ? where v is velocity
Log in to reply
Thanks. Did you solve it the way I did? Also, the friction coefficient here varies over space, but not in time. So the surface is not dynamically updating to reflect the block's status. In your proposed question, would the friction be uniform over space but changing in time, according to the block speed?
Log in to reply
Yes, it would be directly proportional to the speed of the block. More the velocity of the block , more friction offered..
Log in to reply
@Md Zuhair – That sounds like a good question. How about you wait a few days (to give this one a bit of a run) and then post it?
Log in to reply
@Steven Chase – Ya sure. :). No problem
Log in to reply
@Md Zuhair – After posting the problem, Please give the link here @Steven Chase sir
Log in to reply
@Md Zuhair – Are you going to post it, or do you want me to?
Log in to reply
@Steven Chase – It would be better if you post it, I cannot frame a question clearly, If you dont mind :)
Log in to reply
@Md Zuhair – Ok, I will most likely post it today
Log in to reply
@Steven Chase – Ok sir, Thanks :)
Log in to reply
@Md Zuhair – It's up now
@Md Zuhair – I figured you would post it since it was your idea
Nice thought bro, waiting eagerly for Steven sir's problem.
Log in to reply
Its equivalent to somekind of viscous floor...
Log in to reply
@Md Zuhair – Well maybe,lets see.
@Md Zuhair – Hey why is there no activity at slack or here by 2018 aspirants and the IITians too?
It's up now
Cool problem Steven sir , your physics problems are amazing .
Consider an instant in which the box overlaps into the rough region by a distance y . Now as it moves slightly farther into the rough region, an infinitesimal amount of work is done. The total work done by friction is therefore (box length is L ):
W = ∫ 0 L F ( y ) d y
Note that the friction force is a function of the overlap. We must calculate this friction force using calculus, since the coefficient of friction is variable over space.
d m = m L d x d F = μ g d m = α x g d m = α x g m L d x = L m g α x d x F ( y ) = L m g α ∫ 0 y x d x = 2 L m g α y 2
Plugging into the work integral:
W = ∫ 0 L F ( y ) d y = 2 L m g α ∫ 0 L y 2 d y = 2 L m g α 3 L 3 = 6 m g α L 2
Set the work done by friction equal to the initial kinetic energy:
6 m g α L 2 = 2 1 m v 0 2 3 g α L 2 = v 0 2 α = g L 2 3 v 0 2 = 1 0 × 9 4 3 × 2 2 = 2 . 7