Boxed Up
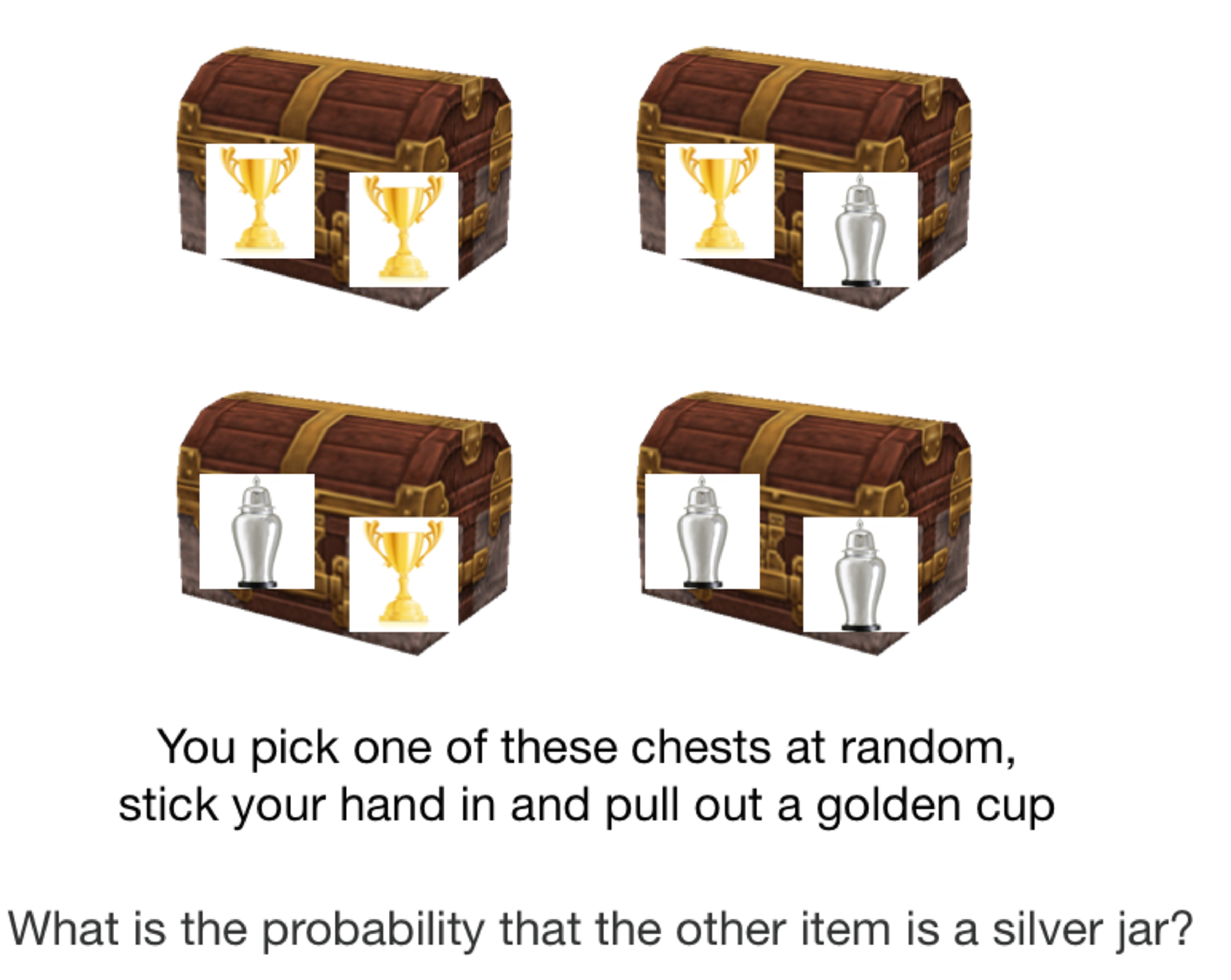
8 identical small boxes and 4 identical chests, each capable of holding 2 of the boxes, are procured. In 4 of the small boxes, a golden cup is placed. In the other 4, a silver jar is placed. The boxes are distributed among the chests as follows:
One chest contains 2 boxes containing golden cups.
One chest contains 2 boxes containing silver jars.
2 chests each contain 1 box with a golden cup and 1 box with a silver jar.
You have been out of the room while the chests have been filled, but have been told by an absolutely honest arbiter about the distribution of the boxes within the chests. You re-enter the room and select a chest at random (you flipped a fair coin twice, assigning one of HH, HT, TH and TT to each chest.) You then flip the same fair coin a third time to randomly select one of the small boxes within the chest. You open this box and find that it contains a golden cup.
What is the chance that the other box in the chest contains a silver jar?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Great problem about conditional probability :)
There are four golden cups you could have selected: G1, G2, G3 and G4.
G1 and G2 are together in a chest. G3 is paired with a silver jar in a second chest, and G4 is paired with another silver jar in a third chest.
Since the choice was made purely by chance, you have 1 chance in 4 of selecting G1, 1 chance in 4 of selecting G2, 1 chance in 4 of selecting G3, and 1 chance in 4 of selecting G4. In 2 of those cases, there is a silver jar in the other box. So the chance of a silver jar is 2/4 = 1/2