Breaking chocolate bar into small squares
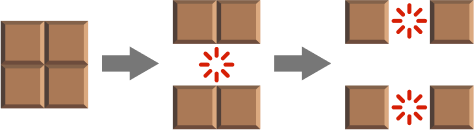
You hear 3 snaps when someone breaks up a 2 × 2 chocolate bar into 1 × 1 pieces, 8 snaps when it's a 3 × 3 bar, and 15 snaps when it's a 4 × 4 bar.
How many snaps will you hear when an 8 × 8 chocolate bar is split into 1 × 1 pieces?

Details and Assumptions:
- You cannot break two or more pieces at once.
- Breaks must be made either horizontally or vertically.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
38 solutions
Very intuitive solution.
Sounds flawed without further explanation but it's still nice.
Log in to reply
Not seeing how it's flawed.
Each crack increases the number of chunks from n chunks to (n+1) chunks. There is always at least one available move. There is no way to increase the number of chunks by more than one.
Geometrically, you have 4 4x4 bars. You hear 60 snaps, which is 4 x 15. You need to hear 3 remaining snaps.
Its actually impossible. as the "condition" is that you cannot break two or more pieces at once, with a caveat that all breaks must be either horizontal or vertical, therefore as the definitions are "bar" and "pieces" (inferring a piece is a 1x1 square) you cannot JUST separate ONE piece. ;-)
Log in to reply
Sure, that's right. With his word piece he doesn't just mean a single piece he means any group of single-pieces, so you get a greater amount of groups of single pieces each time you break the bar, so there must be n-1 breaks to get n groups of single-piecea
Log in to reply
isn't a group of single pieces a "bar". He does actually use the word "bar". just fancied being pedantic today!
Log in to reply
@Brett Jolly – I used the word "piece" for every group of single little pieces, and the word "bar" for the entire chocolate piece. Sorry for the misunderstandings.
You must snap the original grid seven times, and then snap each of the 8 rows/columns 7 times. This gives us 7 + 8 × 7 = 6 3
If you notice the pattern, you might conjecture
If you have an n × n chocolate grid, then you will hear n 2 − 1 snaps to separate the bar into 1 × 1 squares.
Indeed, we can prove this. Using the same logic before, but only generalized: f ( n ) = ( n − 1 ) + n × ( n − 1 ) = n 2 − n + n − 1 = n 2 − 1
For the sake of completeness, the lower bound should also be established.
Log in to reply
I think it is quite obvious that the model is nonsense for n < 1 , so I figured that is not necessary.
Not needed in this case, as it is not establishing f(n+1) from f(n) :) Besides the lower bound n=2 is already established by the problem
I used the same, but then how are we sure this is the minimum number of snaps ? :)
Trying to avoid complications, break the 8 by 8 bar into half, ie two 4 by 8 pieces. That's one snap.
Then, break the two 4 by 8 pieces each into half, that's four 4 by 4 pieces. Two more snaps occurred here.
2 + 1 gives 3 so far.
For each 4 by 4 piece, it's 15 snaps.
15 X 4 gives 60.
60+ 3 gives 63, and there you have it.
2^n - 1 snaps where n is the n*n dimension of the chocolate bar
Wrong. 3x3 doesn’t work.
It would be n^2-1, ;)
Can you prove this?
It's actually (n+1)*(n-1). 2^n - 1 grows way too fast.
Another easier solution is that a 8×8 bar will be four 4×4 bars, after 3 snaps, and each of those 4x4 bars will be 15 snaps. So total 3 + (15×4) =3 +60 = 63
This is especially easy since the problem states the solutions for a 4x4 bar and a 2x2 bar.
I.e. start by considering the 8x8 bar as a 2x2 bar where each of the pieces is actually 4x4 smaller pieces. Dividing up this 2x2 bar takes 3 steps (given in the description).
Now for each of the 4 thus obtained 4x4 bars, we know it takes 15 steps (again from the description). I.e. the total in this step is 4*15=60.
Add up 3 and 60, and we obtain 63.
3, 8, 15... We can notice that we added 5 then 7 then it must be 9 etc. 3, 8, 15, 24, 35, 48, 63, 80... the 8th term is 63.
You cannot assume that the sequence will continue like that.
Nice try my freind
The general solution of the number of snaps for breaking n × n chocolate bar to 1 × 1 pieces is n s n a p s = n 2 − 1 . For n = 8 , n s n a p s = 8 2 − 1 = 6 3 .
Snap the 8x8 in half and each half in half = 3 snaps
Now you have four 4x4 pieces
One 4x4 takes 15 snaps
Therefore 4 x 15 + 3 = 63
If there are n rows given then first we will break all rows by making n-1 snaps and then each column can be split by making n-1 snaps, thus for n rows we will make n (n-1) snaps. Therefore total snaps = n (n-1) + (n-1) = n^2 -1. In this case n =8 So number of snaps = 8^2 -1 = 63
You can break the 8x8 piece into four 4x4 pieces using 3 snaps. The value to break one 4x4 piece is given in the question (15 snaps). Hence, you need 4 ∗ 1 5 + 3 = 6 3 snaps
if we split 8 × 8 into three chocolate bar as 7 × 7 and 1 × 8 and 1 × 7 individually,we hear 2 snaps then, recursion process to resolve problem which split 7 × 7 we hear the 7+8 = 15 times snap when we split into three chocolate bar as 7 × 7 and 1 × 8 and 1 × 7, include split 1 × 8 and 1 × 7 to 1 × 1 into chocolate bar 1 × 1 pieces.
def split(n): if n == 2: return 3 return split(n-1)+2*n-1 print(split(8)) 63
Each round of 3 snaps is capable of dividing a square chunk into even quarters. 3 for the first round plus 4 times 3 for the remaining 4 4x4 blocks, then iteratively again for each of the 16 remaining chunks gices 63. 3+(4 3)+((4^2) 3)=63
A simple Solution is to subtract 1 from the total of the the chocolate bar e.g 8*8=64-1=63 and it also works with other different shaped bars.
A strange solution I found is that if you add one to one side of the multiplywler and subtract one from the other side, it will always work. For instance if you have a 5x5, you adjust it to 4x6=24. I don't know why this works. Maybe soneone can explain?
Given the conditions, for NxN bar, the number of snaps could be shown through the formula (N-1) + N(N-1).
Note that for the NxN bars, the number of columns is N. With this, we can have (N-1) snaps done horizontally and it will give us N pieces of bars wherein each has 1xN dimension. To split all into 1x1 pieces, each bar of 1XN dimension will be cut into 1x1 pieces with N-1 snaps done vertically. Note that we have N bars of 1xN dimension. So, the number of snaps done vertically is Nx(N-1).
Note that the total number of snaps in NXN bar is the sum of snaps done horizontally and vertically.
Horizontally---- N-1 snaps
Vertically------- Nx(N-1) snaps
Thus, the total number of snaps in NxN bar is
(N-1)+N(N-1).
So, for 8x8 chocolate bar, we have
(N-1)+N(N-1)
=7+8(8-1)
=7+8(7)
=7+56
=63 snaps
Y n = (X o-X n) x (X o+X n) + Y o
For X o = 2, Y o = 3, and X_n = givenDimension
I got the answer through (n-1) * (n+1).
When there are 64 squares, the answer is 7*9.
2x2 (=4) -> 3 snaps
3x3 (=9) -> 8 snaps
4x4 (=16) -> 15 snaps
... finding the pattern
n^2 - > n^2 - 1
... so, it can only be 63
8x8 (=64) -> 63 snaps
(L×w)-1= # of snaps Ex (3×4)-1=11 snaps (4×5)-1= 19 snaps
Test it
Breaking a 2×2 chocolate gives us 3 snaps (2×2)-1 Breaking a 3×3 chocolate gives us 8 snaps (3×3)-1 Breaking a 4×4 chocolate gives us 15 snaps (4×4)-1 Therefore, breaking a 8×8 chocolate will give us (8×8)-1 = 63 snaps
One way to break up a chocolate bar is to snap it in half, and snap its halves in half and so on.
This is binary recursive function with l o g 2 ( 8 ⋅ 8 ) = 6 steps where each step contains twice as many snaps as the previous one 1 , 2 , 4 , . . .
Counting the number of snaps, you'll get the geometric progression 1 + 2 1 + 2 2 + . . . + 2 6 − 1
Which will give you S 6 = 1 ⋅ 1 − 2 1 − 2 6 = 6 3
We have 4 grids of 4x4 in a 64 square grid, we already know that for a 4x4 grid it takes 15 snaps so 4x15 for all 4 grids. Now we only need to add the number of snaps to divide the 64 grid into 4 separate grids which is 3. Therefore: 4x15+3=63 snaps for the total
Each piece make one snap, except the final one
2x2 = 4➡️ 4-1 (1 is the final piece) = 3 snaps
3x3 = 9 ➡️ 9-1 = 8 snaps
4x4 = 16 ➡️ 16-1 = 15 snaps
...
8x8 = 64 ➡️ 64 pieces - the final piece = 63 snaps
when there is a 2x2 bar then there are 3 snaps ( 2^2)-1 when there is a 3x3 bar then there are 8 snaps ( 3^3)-1 when there is a 4x4 bar then there are 15 snaps **( 4^4)-1
thus,when there is a 8x8 bar then there are 63 snaps *( 8^8)-1 * thus the answers is 63
- Divide the one 8x8 piece into four 4x4 pieces.. This will take 3 snaps, 1 snap for halfing it into two 8x4 pieces and then 2 snaps for further splitting into four 4x4 pieces.. Now u r given that 15 snaps are required for reducing a 4x4 piece to 1x1. Since u have 4 pieces so 60 snaps plus 3 initial snaps gives u a total of 63 snaps.
If we divide it into four pieces then we get 4×4 type squares Now it is given that a 4×4 square needs 15 sounds So the answer is 15×4+3 Which is 63
n 2 − 1 is the formula ( where n is one side) to calculate the number of snaps!
So, here n = 8 .
∴ , number of snaps = 8 2 − 1 .
Which is 6 4 − 1 = 6 3
we can find thats n ^2 -1
In general...make square of 2,3,4...and then subtract 1....
Let f ( m ) donates the snaps you will hear when a m × m chocolate bar is split into 1 × 1 pieces, then
f ( 2 n ) = 4 × f ( 2 n − 1 ) + 3
by the observation that we can split a 2 n × 2 n chocolate into 4 pieces of 2 n − 1 × 2 n − 1 chocolates by 3 snaps. thus
f ( 8 ) = 4 × f ( 4 ) + 3 = 4 × 1 5 + 3 = 6 3
It takes n − 1 snaps to break an n × n square into n 1 × n rectangles. Furthermore, n − 1 snaps break each rectangle into n 1 × 1 squares. Hence, the number of snaps to break an n × n square into 1 × 1 squares is n − 1 + n ( n − 1 ) = n 2 − 1 . In particular, if n = 8 , the number of snaps is 6 3 .
You need to snap it three times to break it into 4 pieces. Then you need to snap each of those three times to break each block into 4 new pieces. Now you have 16 piece, each of which need 3 more breaks. So, 3 + 3 4 + 3 16.
Simple the bar is 8x8 pieces so 8x8-1
the second assumption - that you can break either horizontaliy or verticaly - make the problem imposible ! look at the 2x2 example - after the first cut - say vertical - you have to cut horizontally and vice versa !
For every increase in n^2 you add the sequential prime number to the total number of snaps from previous answer. 2x2= 3 snaps...3x3= 3+5= 8 snaps.... 4x4= 8+7=15 snaps
Maybe you mean sequential odd number, because the 9 you add from 4x4 to 5x5 isn't prime...
Of course that’s what I meant.. lmao! It was 3 in the morning!!
Solve the recurrence equation T ( n ) = 4 T ( 4 n ) + 3
What is T(1)? What is n?
you mean 4*T(n/2)+3... And what if n is odd?
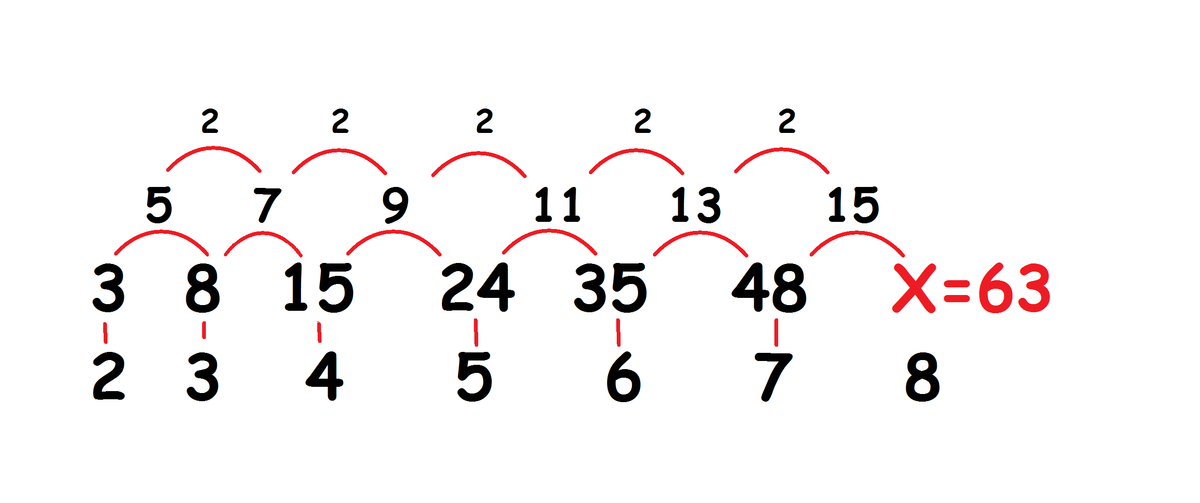
A simple solution is this. At the beginning we have only 1 piece and we have to end up with 64 pieces. Since we make only one extra piece with each cut, we have to cut the bar 6 3 times.