Breezy Trigonometry
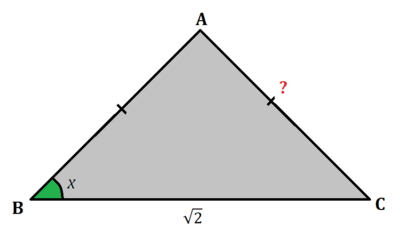
In △ A B C , A B = A C , B C = 2 and ∠ B = x . Find the length of A C , if sin x = 2 2 .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
- FInding angle x
sin ( x ) = 2 2 ⟹ x = 4 5 ∘ [ ∵ x < 1 8 0 ∘ ]
- Since it's an isosceles triangle
∠ A C B = 4 5 ∘ ⟹ ∠ B A C = 9 0 ∘
- Now using Pythagoras' theorem
A C 2 + A B 2 2 A C 2 A C = ( 2 ) 2 = 2 = 1
sin 4 5 ∘ = 2 2 This is a right triangle, so 2 a 2 = 2 2 , so a = 1 .
s i n x = s q r t 2 /2
So cos x= sqrt{(1-(\(sin^2 (x) ))}= s q r t ( 1 − ( 2 / 4 ) ) = s q r t ( 2 / 4 ) = s q r t 2 /2
Let AC=AB=y Now by Law of Cosine (AC)^2=((AB)^2)+((BC)^2)-(2xABxBCx(cos(x)))
So (y^2) = (y^2) + 2 -(2 sqrt(2) y*(sqrt(2)/2)) 2y=2
Giving y=1 So AC=1
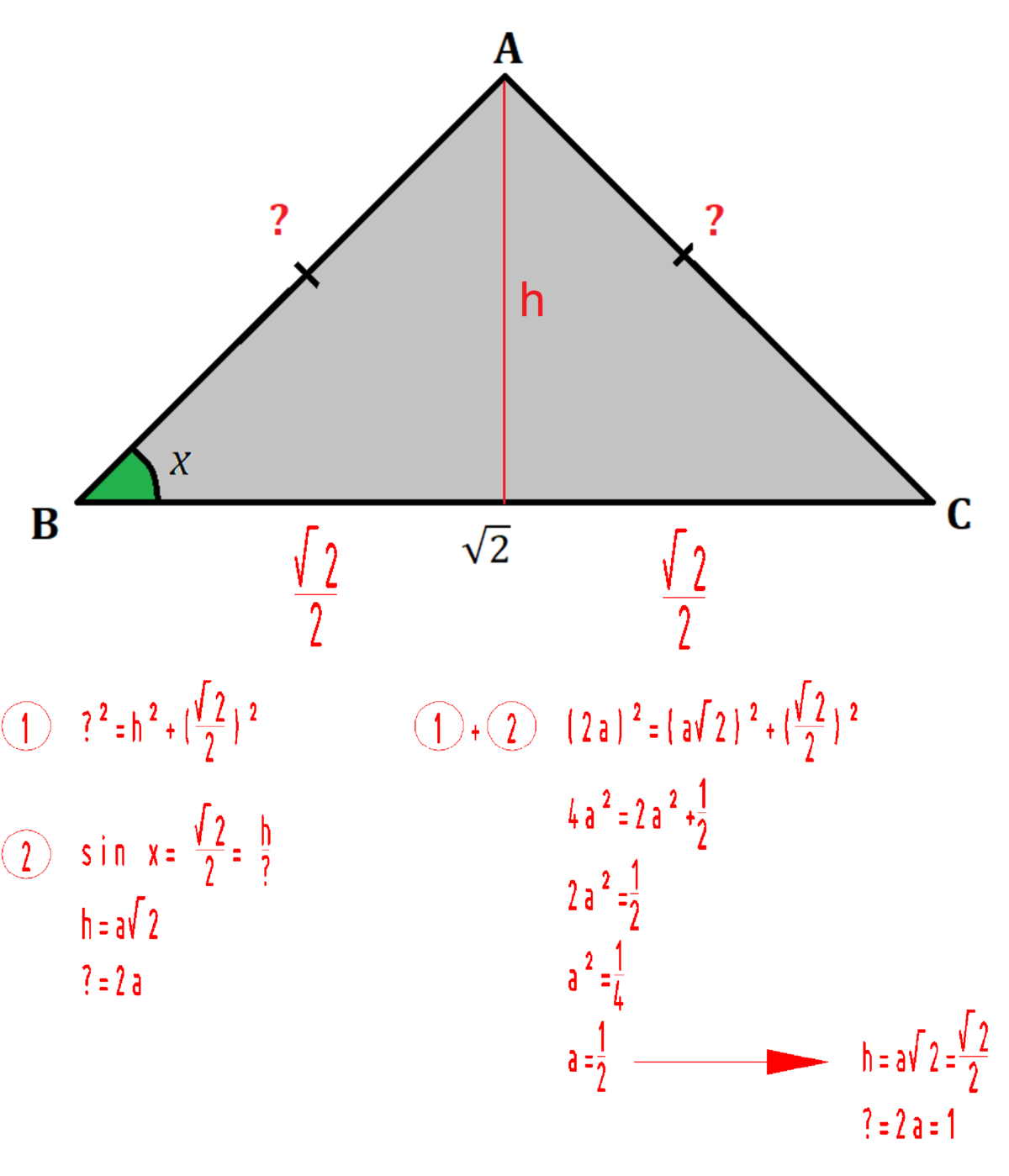
Here is a method of solving the problem without finding the angle x.
First, let's add a midpoint M of Segment B C . With A M perpendicular to B C , you get two identical right triangles △ A B M and △ A C M .
Then, we find the measure of B M
B M = C M
B C = B M + C M
B C = 2 B M
B M = 2 2 .
With that, by definition of sine,
sin ( x ) = A B B M
2 2 = A B 2 / 2
A B = 2 / 2 2 / 2
And finally, A B = A C = 1
That's a great alternative solution!
Thank you.
\sinx = \frac{opposite catheter}{hypotenuse} = \frac {\overline{AC}}{\sqrt{2}} = \frac {\sqrt{2}}{2} _therefore_ \overline{AC} = \frac {\sqrt{2} * \sqrt{2}}{2} = \frac {2}{2} =1
fix your latex
sin x = h y p o t e n u s e o p p o s i t e = 2 A C = 2 2 t h e r e f o r e A C = 2 2 × 2 = 2 2 = 1
Log in to reply
@Percy Jackson make a separate solution so people can see without having to do anything.
This is how you fix your Latex, Blayde
Log in to reply
'Ass' what Percy Jackson
Log in to reply
his name says it
you typed a double bracket in the ac/root 2 part. notice?
We need not consider anything but the fact that triangle is isosceles, let the missing length A C be a , by Pythagoras theorem,
a ² + a ² = ( 2 ) 2 → a ² = 1
Or a = 1
sin x = 2 2 ⇒ x = 4 5 ∘
By law of sines,
A C sin ∠ A B C = B C sin ∠ B A C
A C sin x = 2 sin ( 1 8 0 − 2 x )
A C sin 4 5 = 2 sin 9 0
A C = sin 9 0 2 × sin 4 5 = 1 a n s w e r
sin x = √ 2 1 So, we know if sin θ = 2 1 then , θ = 4 5 ° ± 2 π n
Now as in this case, 0 ° ≤ x ≤ 9 0 °
So, x = 4 5 ° So, ∠ B A C = 9 0 °
Now by Sine Rule,we know sin 4 5 ° A C = sin 9 0 ° B C
→ 2 1 A C = 2
→ A C = 1 u n i t s
In a right isosceles triangle, if the legs are x, then the hypotenuse is x 2 . So in this question, we are given the hypotenuse, so the legs are 2 2 , which is 1.
who else had come from his link n todays (26 or 25/7/20)???
It is well known that sin 4 5 = 2 2 . So x = 4 5 ° . The triangle is isosceles, meaning that angle A C B is 4 5 ° too, hence angle B A C = 9 0 ° .
We now know that this is a right-angled triangle.
Let the side length A C be known as y , for now. Using Pythagoras:
y 2 + y 2 = ( 2 ) 2
2 y 2 = 2
y 2 = 1
y = 1
So the answer to this question is 1.