Bridge Current
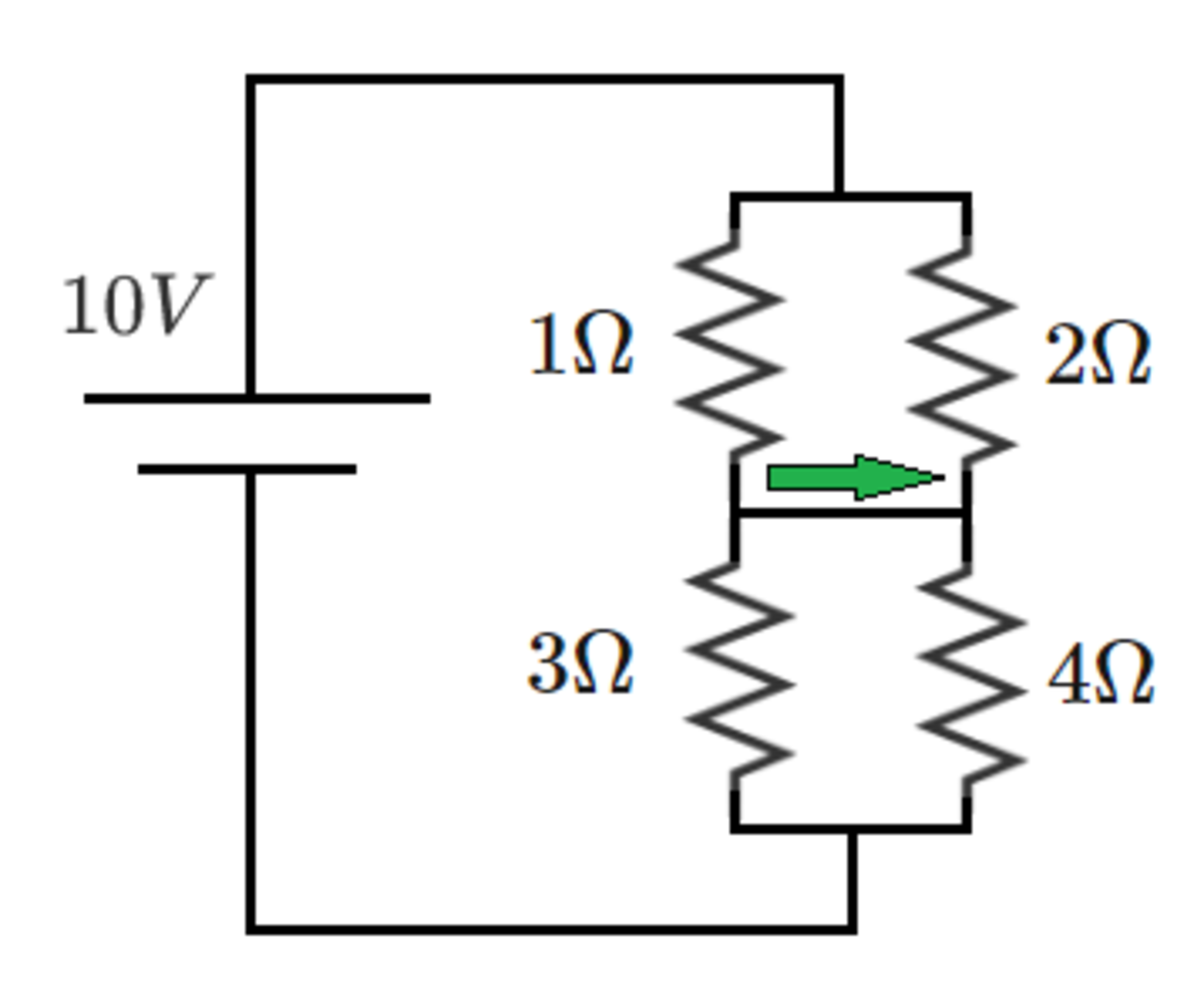
What is the magnitude (absolute value) of the current in the bridge (shown as a green arrow in the diagram)?
The answer is 0.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nice solution. The key being that since the bridge has no resistance, there is no voltage drop so one can imagine the bridge being shrunk to zero length, which is how one gets the 1||2 in series with the 3||4. Also note that the problems become much harder to solve if CD contains a resistor.
Log in to reply
You can draw it on paper and post. I will help to put it in a proper diagram.
Do you want to post the harder version?
Log in to reply
I made up a problem to post. Never posted anything before. Either today or tomorrow. But what do you use to make the diagram?
Log in to reply
@Richard Costen – MS paint. Ha ha
Log in to reply
@Steven Chase – I finally found a circuit diagram application that I could use the create the diagram. Most of the apps I tried wouldn't allow for 4 5 ∘ rotations of components. I just posted the problem now. Hope my first attempt at posting is ok. Btw, one of my daughters did amazing things with MS paint, so now there are at least two experts at using it. :)
Log in to reply
@Richard Costen – Yeah, Paint is actually not bad for simple things. Nice problem, too.
@Richard Costen – You may post the hand drawn images as well. Just draw the circuit on a paper, take a pic and upload it.
The resultant resistance in series with the 10 V voltage source R A B = ( 1 ∣ ∣ 2 ) + ( 3 ∣ ∣ 4 ) = 1 + 2 1 × 2 + 3 + 4 3 × 4 = 3 2 + 7 1 2 = 2 1 5 0 Ω .
The current through the voltage source I = 2 1 5 0 1 0 = 4 . 2 A.
By current division, the currents through the 1 Ω and 2 Ω are I A C = 3 2 × 4 . 2 = 2 . 8 A and I A D = 3 1 × 4 . 2 = 1 . 4 A.
Similarly, I C B = 7 4 × 4 . 2 = 2 . 4 A and I D B = 7 3 × 4 . 2 = 1 . 8 A.
Therefore, I C D = I A C − I C B = 2 . 8 − 2 . 4 = 0 . 4 A.
Note that I A D + I C D = I D B , which is true as 1 . 4 + 0 . 4 = 1 . 8 A.