Brilli The Ant is Back!
A
12
feet high room is
40
feet long and
10
feet wide. Brilli the ant is standing in the middle of one of the walls (which is
10
by
12
feet), such that it is
1
foot above the floor, and is equidistant from the other
2
edges of that wall.
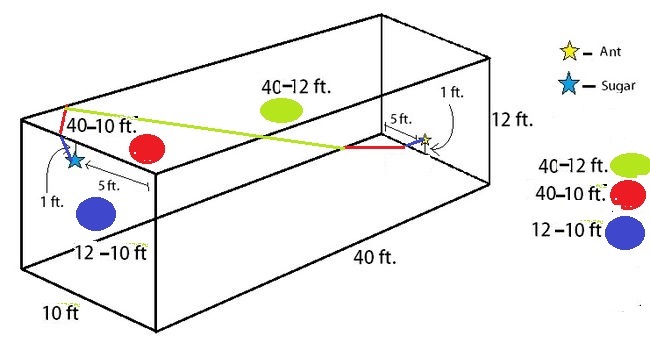
In the middle of the wall opposite to Brilli's, rests a sugar crystal, 1 foot below the ceiling. The minimum distance Brilli needs to cover to reach the sugar crystal, assuming that Brilli can walk anywhere inside the room, is x . Determine the value of x 2 .
Image credit: Flickr Snap
The answer is 2248.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How can the ant traverse the wall is he the shadowcat ??
2248 is correct! :-)
2248 is correct. Here are some of the paths. The path in green color is the shortest.
Imgur
It's funny because in the shortest path, the ant will walk to the floor and to the ceiling that seems it's fooling around before getting to the sugar.
How do you know that that is the shortest path? You only showed how to get it but how do you know that there is no shorter way?
Log in to reply
True, I didn't show that, but one can see that by observing all of the different 'rectangle configurations' (configurations of the walls/roof/floor rectangles) and seeing that any other way will make it shorter.
I might put the proof here in the near future.
Log in to reply
But there are infinitely many paths the ant can take
Log in to reply
@Nathan Ramesh – So? Between any two points in a Euclidean space, there are an infinite number of curves with endpoints at those two points, but only one is the shortest. That shortest one is called the line-segment joining those two points.
There are an infinite number of paths for Brilli, but only one is the shortest.
Log in to reply
@Milly Choochoo – Then how did you examine all possible cases?
Log in to reply
@Nathan Ramesh – Well I (we) know that the shortest path is going to certainly be a straight line in the ant's perspective, so we need only consider straight lines (with the sides/roof/floor laid out, just as in my solution). If you start to check the different straight-line paths, you'll realize that all of them are just different ways that the ant can spiral around the room (the longest walls, the roof, and the floor) before getting to the sugar. For example, the simplest straight-line path in which the ant goes directly straight down that room to the sugar (52 feet), there is no spiral. The shortest path will happen when the ant does half of a spiral, which is exactly what is going on in the solution. If the ant does any more spirals to get to the sugar, it will be longer than the shortest path.
Log in to reply
@Milly Choochoo – But for example, there are multiple ways the ant can start out on the floor (the way in the solution and a way that is 54 long). However they are both straight lines in the ants perspective.
Log in to reply
@Nathan Ramesh – Yes, however when unwrapping the room into its net we see that the essential path isn't actually a straight line. He is checking all possible actual straight line paths and seeing which one is the shortest.
If you refold it back to origininal shape of cube,the transverse line will be transformed to a straight line...
Wow... This is the best solution I've seen on Brilliant yet (and I've been here almost since launch). This is what back in the days (before all the unnecessary updates) you'd call a "Legendary Solution." You even provided excellent illustrations of the solution!
Great work.
I still didn't get it... sorry about that But how can the ant go diagonally?
Could you post a 3d diagram of the path...
sir, how can one be sure that the answer that he got is correct? i got 2600, how can i check whether it is the smallest?
I nearly got it:( Had 2372.
You have shown the last step from the right. should it not be from the left ?
Second observation. Because of symmetry the ant must pass through the midpoint of 10
40 or 12
40.
Third one. As pointed out, maximum=2 * minimum. Why? Does it apply if there is no symmetry?
Minimum distance should be √2600
Log in to reply
precisely sir....
Log in to reply
We obviously not! I just showed how you can get a shorter distance!
Its 2600....2248 is totally wrong
The shortest distance will be
x 2 = 4 2 2 + 2 2 2
x 2 = 2 2 4 8
please explain how
Log in to reply
I do not know how to draw the figure in this website. I cant attach my drawing either. I hope this will help. It is a triangle with the hypotenuse x .
One leg of the triangle will be = 6 + 1 0 + 6
and the other will be = 1 + 4 0 + 1
courtesy of Pythagoras,
x 2 = ( 1 + 4 0 + 1 ) 2 + ( 6 + 1 0 + 6 ) 2
Brilli can crawl from his initial position to the sugar's location DIAGONALLY
40+1+1 which side and 6+6+10 which side and how
Log in to reply
Find the attached drawing of Milly Choochoo
This one was way too easy to be level 5.
To solve this problem, you absolutely must understand that because the ant is walking along the walls, all of those pinching corners and edges can be considered as the line separating one surface of the room from another (or others for an edge). This means that if the ant were to go about walking in all sorts of directions, going upside down, sideways, backwards, or any other way, we can ignore those weird directions and just consider the ant moving in one flat plane, sort of like a POV (point of view) perspective.
The assumed shortest distance to jump to very quickly (and by now you should know that answers like those are never correct on Brilliant) is 5 2 f t . - straight down to the floor, straight across the floor, and straight up to the sugar. That seems like the shortest straight line we can draw from the starting point to the ending point while staying on the walls, right? Nope, it isn't. You need to think about the possibility of traversing on the other walls.
After thinking and working that out for a bit, you'll arrive at the final answer.
And so...
x = 2 2 4 8 ⟹ x 2 = 2 2 4 8