Brilliant Logo Triangles
The Brilliant.org logo is based on the disdyakis triacontahedron, which forms 15 great circles when projected onto a sphere, exhibiting both icosahedral and dodecahedral symmetries.

Any 3 points on the sphere which satisfy the following conditions
1) Each point is the intersection of 2, 3, or 5 of the great circles
2) Each pair of points lie on 1 of the great circles
3) Not all three points lie on any 1 of the great circles
shall be counted as 1 [spherical] triangle. How many triangles are there in the spherical disdyakis triacontahedron?
Below is the stereographic projection of the spherical disdyakis triacontahedron. One of the points is at infinity.
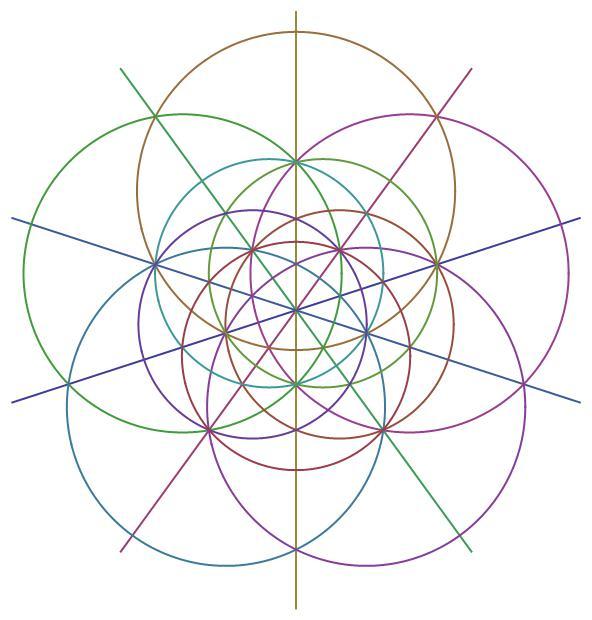
Note: The disdyakis triacontahedron is the largest Catalan solid with 120 identical faces, which is the maximum any polyhedron can have.
Follow-up notice: Some have questioned about the fact there can be more than one possible spherical triangle, given 3 arbitrary points on a sphere. That is the reason why it's been stated that any such unordered set of 3 points meeting the conditions 1-3 shall count as ONE spherical triangle. Hence, it becomes more of a problem in combinatorics rather than geometrical, although a good understanding of geometry helps.
2nd Follow-up notice: ( 3 6 2 ) = 3 7 8 2 0 is not the answer, as it would violate conditions 2) and 3). The great circles are limited to the 15 noted.
The answer is 3080.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Jon, this is a wonderful proof of the answer, much better than the bashy approach I took to get this done. This is mathematics like how it should be done. It's rare that I ever see you post solutions, but when you do, well, it's memorable.
Log in to reply
Thank you for the kind comments! You always post interesting problems, and I enjoy working on them.
Oh my, I spent hours on this problem bashing out each case, checking and rechecking (and also getting it wrong once because the first time I saw the problem I thought that multiple spherical triangles can be created from 3 points)
And then you come and give an elegant solution. Kudos for that. The only thing I'm disappointed about is that I can only give one upvote.
Oh! My! God! It deserves > 1000 upvotes
There are 3 kinds of points on the spherical disdyakis triacontahedron, those that are at the intersections of 2 , 3 , and 5 lines. Hence, all triangles can be categorized by such points as vertices, and counted separately. Below is the list of the number of triangles of each, and the grand total.
{
2
,
2
,
2
}
0
4
0
{
2
,
2
,
3
}
0
0
0
{
2
,
2
,
5
}
0
0
0
{
2
,
3
,
3
}
0
0
0
{
2
,
3
,
5
}
9
6
0
{
2
,
5
,
5
}
4
8
0
{
3
,
3
,
3
}
0
0
0
{
3
,
3
,
5
}
4
8
0
{
3
,
5
,
5
}
9
6
0
{
5
,
5
,
5
}
1
6
0
T o t a l 3 0 8 0
As an example, for { 5 , 5 , 5 } triangles, if we disregard condition 3), and noting that every { 5 } point lies on a great circle with any other { 5 } point, then we can compute the total number of triangles
( 3 ) ( 2 ) ( 1 ) ( 1 2 ) ( 1 1 ) ( 1 0 ) = 2 2 0
However, there are 6 pairs of { 5 } points that are antipodal, so that for each such pair, there are 1 0 triangles (sets of 3 points, technically) that all fail to meet condition 3), so that the net is
2 2 0 − 6 0 = 1 6 0
As another example, there are no { 3 , 3 , 3 } triangles, which can be determined by inspection of the stereographic projection.
Since there are 62 vertices on the disdyakis triacontahedron , shouldn't the answer be ( 3 6 2 ) ?
Log in to reply
That would violate conditions 2) and 3). Yes, that would be the maximum possible, if we simply drew in great circles between any pair of points, but the problem restricts the great circles to the 15 noted.
Messy casework is (not) the way to go.
(BTW, if you add up all the numbers, you get twice the correct answer, because this is my scratch paper for the first wrong answer that I submitted)
Oh, you mean you almost had it right, but was off by a factor of 2?
Yeah, it's messy all right, when done in the bashy way. Lots of pitfalls.
I spent most of my time trying to recreate the Brilliant.org logo in the mathematically correct form, and then I hurried up with finding the answer by making me about a dozen copies of the stereographic projection and looking at each case. Yes, it's a mess. As soon as I had the answer, I posted the problem.
Of course I was very happy to see Jon's proof, putting the matter to rest.
Log in to reply
A slight extension is to drop the restriction where only one spherical triangle can be made from three vertices.
Log in to reply
Well, given 3 arbitrary points not all on the same great circle, shouldn't we be able to form 8 spherical triangles from them? That is 2 to the 3rd power?
Log in to reply
@Michael Mendrin – Yep, for each side A B (which I will define as the arc A B of that certain circle), we can either choose the minor arc or the major arc. This gives 2 3 = 8 circular triangles.
Log in to reply
@Daniel Liu – Let me do say that I had almost posted the incorrect answer originally, but luckily I caught myself. I can get paranoid about that sometimes. But you, too, managed to hit on the right number. Congrats.
I always wanted to post a question on brilliant logo. I see that this question simply rocks. Nice work!
Log in to reply
Yeah bro, I too just posted a problem on brilliant's logo which is a little inspired by this problem.
Log in to reply
@Shreyansh Mukhopadhyay – yeah and I blew it, I think...? I need to review your careful answer to that problem.
Log in to reply
@Michael Mendrin – Yes, that is needed to be done carefully. Even I too caught my answer to be wrong after posting the question, so I edited the question a little. It was great that none had attempted the problem at that time.
Let { A , B , C } be a set of three points, as described in the problem. Then A and B lie on some great circle (say γ C ), A and C lie on some great circle (say γ B ), and B and C lie on some great circle (say γ A ). So, we can count the number of possible sets { A , B , C } by counting the number of ways to choose three great circles.
There are 15 great circles, so there are ( 3 1 5 ) = 4 5 5 ways to choose three of them. However, we must exclude the cases where all three great circles pass through the same pair of antipodal points.
There are 12 points that lie on exactly five great circles, 20 points that lie on exactly three great circles, and 30 points that lie on exactly two great circles.
Among the 12 points that lie on exactly five great circles, there are six pairs of antipodal points. For each such pair of antipodal points, there are ( 3 5 ) = 1 0 ways to choose three great circles that go through the points. Among the 20 points that lie on exactly three great circles, there are ten pairs of antipodal points. For each such pair of antipodal points, there is ( 3 3 ) = 1 way to choose three great circles that go through the points. (We can ignore the 30 points that lie on exactly two great circles.) This gives us a total of 4 5 5 − 6 ⋅ 1 0 − 1 0 ⋅ 1 = 3 8 5 viable ways to choose three great circles. Call them γ A , γ B , and γ C .
Then there are two ways to choose the point A (from the two intersections of γ B and γ C ), two ways to choose the point B , and two ways to choose the point C , so the number of sets { A , B , C } is 8 ⋅ 3 8 5 = 3 0 8 0 .