Brilliant's Brilliant LOGO

One heavy-handed approach uses Mathematica, which contains the data for the Disdyakis triacontahedron graph. If we take the Laplacian matrix $\Gamma$ for that graph, and construct the Moore-Penrose pseudoinverse $\Gamma^{-1}$ , then the effective resistance between vertices $u$ and $v$ on the graph is $\Omega_{u,v} \; = \; \Gamma^{-1}_{u,u} + \Gamma^{-1}_{v,v} - \Gamma^{-1}_{u,v} - \Gamma^{-1}_{v,u}$ Mathematica tells me that the effective resistance between opposite vertices of valency $10$ is $\tfrac{139}{362}$ (while the effective resistance between opposite vertices of valency $6$ is $\tfrac{20723}{38010}$ , while the effective resistance between opposite vertices of valency $4$ is $\tfrac{5525}{7602}$ ).

As a different presentation, consider the particular case where we want the effective resistance between opposite vertices of valency $10$ . We can use the star-mesh transform to remove all the vertices of valency four, since a "star" of valency $4$ is equivalent to a mesh consisting of resistance of $4 \; \Omega$ joining every two of the four end-points. Thus, combining parallel wires, the starting network is equivalent to one consisting of an icosahedron, where each edge has a resistance of $4\;\Omega$ , and a dodecahedron, where each edge has a resistance of $4\; \Omega$ , where icosahedron and dodecahedron vertices are connected by a rhombic triacontahedron of wires of resistance $\tfrac23 \; \Omega$ . To determine the effective resistance between an opposite pair of valency $10$ vertices, we need to go through a process of identifying equipotential vertices by symmetry. Equipotential vertices are shorted together, as usual, and the combined effect of parallel resistances between the shorted vertices is determined. As a result, we obtain that the effective resistance between an opposite pair of valency $10$ vertices is the effective resistance between $A$ and $B$ of the network shown here, where the resistance (in Ohms) of each wire is shown. The nodes coloured red derive from dodecahedral vertices, while the nodes coloured green derive from icosahedral vertices. Note that the two wires in the middle do not meet each other - they pass over each other without contact.

A relatively simple (well, it involves solving $14$ simultaneous equations in $14$ variables) calculation confirms that the effective resistance between $A$ and $B$ is $\boxed{\tfrac{139}{362}} \,\Omega$ .

Relevant wiki: Transformation of Resistances (Star to Delta and Delta to Star)

Observe that the polyhedron consists of many triangles like the one given below.

And every outer edge of each triangle is shared by $2$ triangles in a parllel way. So when we separate the triangle we double it and half the resultant edge to make it an icosahedron.

Note that Icosahedron is similar to Disdyakis triacontahedron. The difference is that all triangle faces are simple equilateral triangle. So try to convert this triangle to a simple triangle.

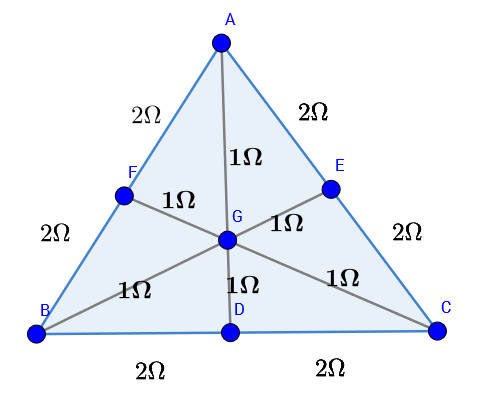
Convert the junctions $E,D,F$ into Deltas. Then further convert the junction at point $G$ into delta. You will get a simple triangle with a resistance of $\frac{8}{5}\Omega$ on each edge.

Now half this value(since two equal egdes in parellel are replaced by a single resistance) of to get a resisitance $r=\frac{4}{5}\Omega$ between two adjescent nodes of an icosahedron given below.

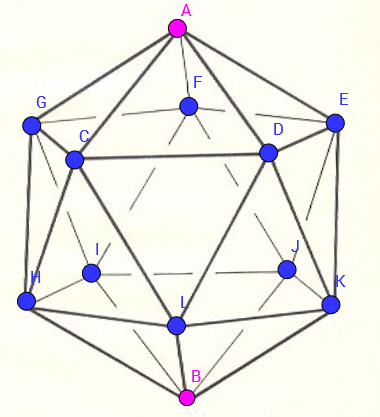
Now observe, that by symmetry the potentials at points $G,C,D,E,F$ are equal. So no current will flow from $GC,CD,DE,EF,FG$ .

So we can join the points $G,C,D,E,F$ .

Similarly, the potentials at $H,I,J,K,L$ are equal. So no current will flow from $HI,IJ,JK,KL,LH.$ So these points can also be joined.

So the circuit simplifies to:- 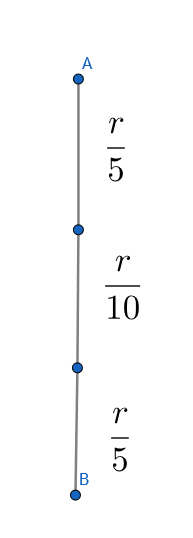Now from A to B, the resistances are in series, so adding them gives $R=\frac{1}{2} r$

We know that $r=\frac{4}{5} \Omega.$

So putting this we get $R_{eq}=\boxed{\frac{2}{5}\Omega}$ .

NOTE:-This solution is incorrect. As a bonus question find the step where I made a mistake which made me get my answer wrong.

I managed this with a bit of thought about symmetry and counting the edges. So from either pole to the 'arctic circle pentagon' there are ten links. So each of those legs contribute 0.1 Ohm. From the previous 'arctic pentagons' to the 5 apexes in the northern and southern hemispheres there are 20 edges so both of those contribute 0.05 Ohm each. The next stage is rather less clear. I estimated that there are 25 edges in total leaving both sets of the 5 apexes and every crossing takes 2 edges. So that 2/25 = 0.08 Ohm for the middle. I reckon it might be a little low since some edges are used twice, nevertheless there are also some extra edges. So all in all I estimated $\boxed {0.38}$ , which was within the error band permitted.
This is an example of an engineering approach, good estimates are often as valuable as the theoretic exact answers.

Disdyakis triacontahedron can be created out of Dodecahedron by dividing each face in 10 triangles. Dodecahedron have has a top and bottom pentagon face and the centers of these are the vertices between which we have to calculate the resistance.

In the diagram below, the green region is the half of the pentagon in the upper half of the Dodecahedron and the red region is the half of the pentagon in the lower half of the Dodecahedron. Potential is written in box and the edge number in circle, so let the current in the direction of the arrow in edge number $n$ is $i_n$ . Because of the cyclic and mirror symmetries involved, this strip can be copied 10 times and pasted adjacently to make the Disdyakis triacontahedron. And the voltages in the middle vertices are derived from the mirror symmetry at the middle horizontal plane. As each of the edge has resistance $1 \Omega$ , so the current passing through an edge and the potential difference across it are equal and I will use them interchangeably throughout the solution.

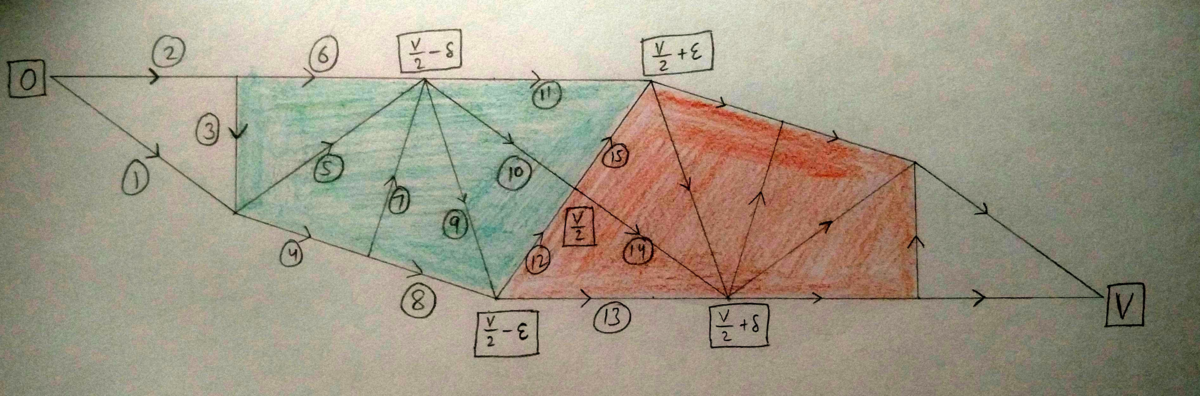
Now for the applied voltage $V$ , let's say current produced is $I$ . So,

$I = 5(i_1 + i_2)$

and

$\frac{V}{2} = i_2 + i_6 + i_9 + i_{12}$

The currents $i_3$ to $i_9$ can be obtained in terms of $i_1$ and $i_2$ using easy applications of Kirchhoff Voltage Law and Kirchhoff Current Law,

$i_3 = i_1 - i_2$

$i_4 = 9 i_1 - 10 i_2$

$i_5 = 4 i_2 - 3 i_1$

$i_6 = 3 i_2 - 2 i_1$

$i_7 = 14 i_2 - 12 i_1$

$i_8 = 33 i_1 - 38 i_2$

$i_9 = 45 i_1 - 52 i_2$

From the known potentials in the middle vertices, we know,

$i_{13} = i_{11}$

$i_{12} = i_{15}$

$i_{10} = i_{14}$

By Kirchhoff Current Law,

$i_6 + 2 i_5 + 2 i_7 = 2 i_9 + 2 i_{10} + i_{11}$ and $i_8 + 2 i_9 = 2 i_{12} + i_{13}$

Writing the above relations in terms of $i_1$ , $i_2$ and $i_{12}$ ,

$4 i_{12} = 299 i_2 - 257 i_1$ and $2 i_{12} = 39 i_1 - 45 i_2$

These can be solved to give,

$i_1:i_2:i_{12}::389:335:48$

Finally, the resistance -

$R = \frac{V}{I} = \frac{2(i_2 + i_6 + i_9 + i_{12})}{5(i_1 + i_2)} = \frac{2(43 i_1 - 48 i_2 + i_{12})}{5(i_1 + i_2)}$

$R = \frac{2(43*389 - 48*335 + 48)}{5(389 + 335)} = \frac{139}{362} \approx 0.384$

Using Wolfram Mathematica 11.3 in a heavy-handed approach (I agree with Mark Henning), the answer is $\frac{139}{362}\Omega$ .

$\text{vertices}=\text{PolyhedronData}[\text{DisdyakisTriacontahedron},\text{VertexCount}];$

$\text{edges}=\text{PolyhedronData}[\text{"DisdyakisTriacontahedron}",\ "\text{Edges}"];$

Looking for the vertices with 10 edges:

$\text{poles}=\text{Select}[\text{Tally}[\text{Sort}[\text{Flatten}[\text{edges}]]],\text{\$\#\$1}[[2]]=10\&]^T[[1]] \Rightarrow {23,24,25,32,33,34,57,58,59,60,61,62}$

Looking for 1--edged vertices at maximal graph distances:

$\text{Select}[\text{Flatten}[\text{Table}[\{i,j,\text{GraphDistance}[g,i,j]\},\{i,\text{poles}\},\{j,\text{poles}\}],1],\text{\$\#\$1}[[3]]=6\&] \Rightarrow \left( \begin{array}{ccc} 23 & 61 & 6 \\ 24 & 62 & 6 \\ 25 & 60 & 6 \\ 32 & 59 & 6 \\ 33 & 58 & 6 \\ 34 & 57 & 6 \\ 57 & 34 & 6 \\ 58 & 33 & 6 \\ 59 & 32 & 6 \\ 60 & 25 & 6 \\ 61 & 23 & 6 \\ 62 & 24 & 6 \\ \end{array} \right)$

$g=\text{Graph}[\text{Range}[\text{vertices}],\text{edges}];$

$\text{resistance}=\text{With}\left[\left\{\Gamma =\text{PseudoInverse}\left[\text{With}\left[\{\text{wam}=\text{WeightedAdjacencyMatrix}[\text{\$\#\$1}]\}, \\ \ \ \text{DiagonalMatrix}\left[\text{Tr}\text{/@}\text{wam}^T\right]-\text{wam}\right]\right]\right\},\text{Outer}[\text{Plus},\text{Diagonal}[\Gamma ],\text{Diagonal}[\Gamma ]]-\Gamma -\Gamma ^T\right]\&;$

Extracting the requested resistance from the complete effective resistance table:

$\text{resistance}(g)[[23,61]]\Rightarrow \frac{139}{362} \approx 0.383977900552486$

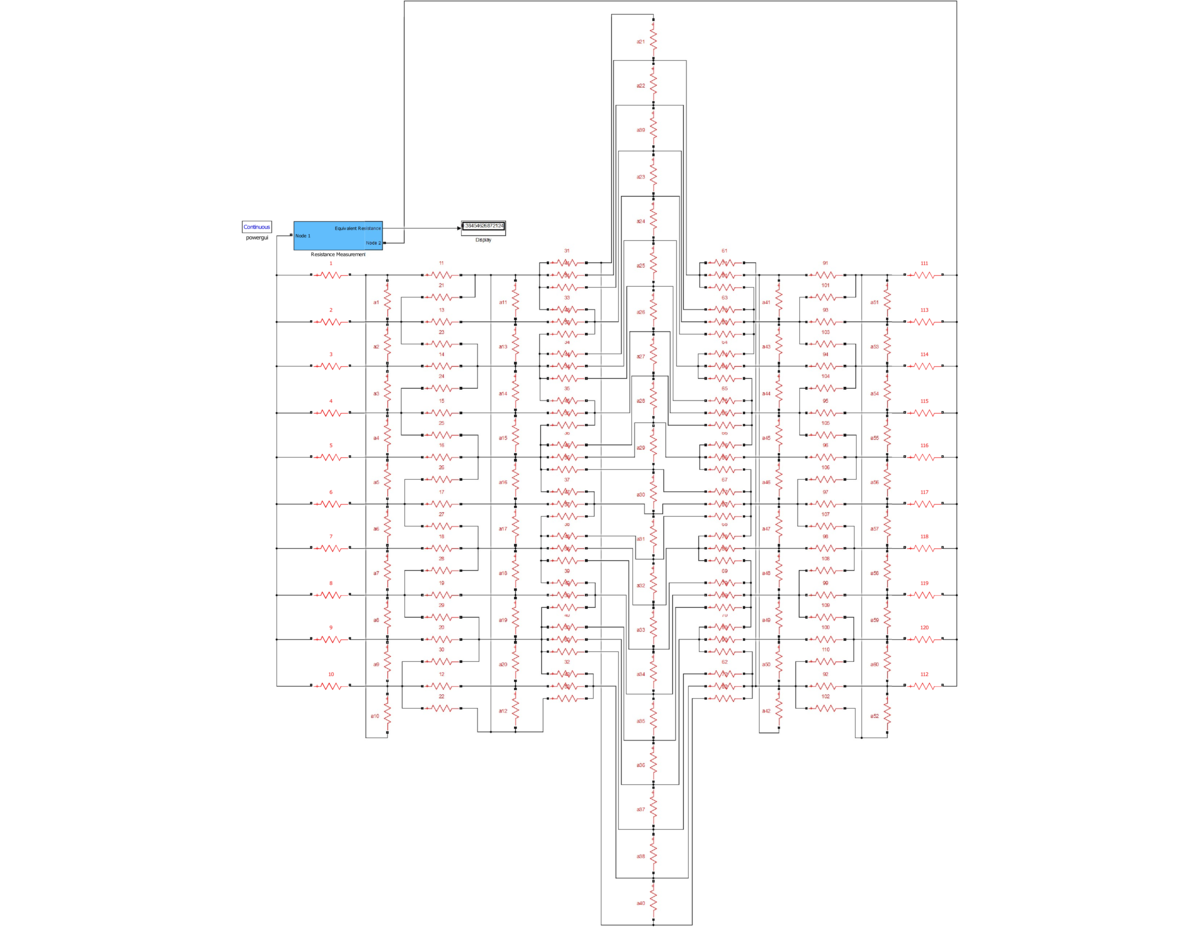
I just went all in with Simulink: