Broadcasting a message in a fully connected network

Computer Science Level 3

In a fully connected network with $n$ nodes, the number of direct links between all pairs of computers is $\frac {n(n-1)} 2.$ For $n = 2000$ , find the minimum time required to broadcast a message stored in $P_1$ to all other computers in the network. Assume that

sending a message from a computer to another computer takes $10^{-6}$ sec;
any computer can send only one message to any other computer at a time.

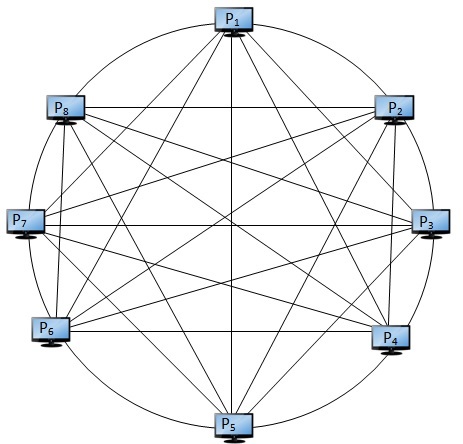
Here is an example of fully connected computers with 8 computers.

11 \times 10^{-6}

sec

1.9

sec

1

sec

20 \times 10^{-6}

sec

500 \times 10^{-6}

sec

2 solutions

Ossama Ismail
Jan 26, 2017

We will show that at each iteration, the number of computers in the network who have received the message can be doubled. To do this we do something like this:

step1: $P_1$ sends message to $P_2$

step2: $P_1$ and $P_2$ send messages to $P_3$ and $P_4$

step 3 : $P_1, P_2 , P_3$ and $P_4$ send messages to $P_5, P_6 , P_7$ and $P_8$
...

Because we're doubling the number of computers each time (except for maybe the last step), the number of steps is $\lceil \log_2 n \rceil$ .

So, to send out this message to 2000 computers it takes $\lceil \log_2 2000 \rceil$ time units.

Formally, we could do this:

Computer $P_1$ sends the message to $P_2$
for i = 0 to (log n – 1) do
for j = $2^i$ +1 to $2^{(i+1)}$ do in parallel or simultaneously
$P_{(j - 2^1)}$ sends message to $P_j$
end for j
end for i

Can you explain why this algorithm works, how you came up with it and why this gives the proposed time?

Agnishom Chattopadhyay - 4 years, 4 months ago

This is an Order of $log_2(n)$ algorithm. If you trace the given algorithm you will get the following:

step1: $P_1$ sends message to $P_2$

step2: $P_1$ and $P_2$ send messages to $P_3$ and $P_4$

step 3 : $P_1, P_2 , P_3$ and $P_4$ send messages to $P_5, P_6 , P_7$ and $P_8$
...

With each step, the number of the computers is doubled or it goes

$1,2^1,2^2,2^4, \dots, 2^k$ where $k = log_2(n)$

Ossama Ismail - 4 years, 4 months ago

Thanks, that really helps. I have added that to the solution so that the solution is more clear to the reader

Agnishom Chattopadhyay - 4 years, 4 months ago

How can we show that this is indeed the optimal algorithm?

Agnishom Chattopadhyay - 4 years, 4 months ago

Here we are dealing with a parallel algorithm where we are trying to make use all computers at the same time.

To solve this problem sequentially, it requires O(n) time. To satisfy the optimality when using parallel processing the cost of the algorithm must equal O(n).

Cost of parallel algorithm = runtime $\times$ no of computers = $log_2(n) * n = nlog_2 n \gt n$

This algorithm is not optimal...

Ossama Ismail - 4 years, 4 months ago

I do not think we need to multiply with # of computers here. We are only asked to minimize the running time, right?

Agnishom Chattopadhyay - 4 years, 4 months ago

@Agnishom Chattopadhyay – Yes, we are asking for minimum time. But the answer to your question about optimality. This is not optimal.

Ossama Ismail - 4 years, 4 months ago

@Ossama Ismail – What is your definition for optimality?

Agnishom Chattopadhyay - 4 years, 4 months ago

@Agnishom Chattopadhyay – When using parallel computers or processor the definition of optimality is:

the best sequential time(one processor) = no. of processor x (parallel run time )

if you satisfy the above equation then your algorithm is optimal. If not then you must achieve speed up.

Here we achieved to speed up, because the run time is o(log(n)) which is better than O(n) in the case of using one processor to send the message to n processors.

Ossama Ismail - 4 years, 4 months ago

Saya Suka
Jan 25, 2017

We will get minimized time when all computers keep repeating the message to another which is still ignorant of it, once the message reach them. So the number of computers that would have gained the knowledge after each round of 'data-sharing' will double than the number before. Since 2000 is less or equal than 2^11 (more like 2^10 < 2000 <= 2^11), thus it will need 11 rounds of sharing / broadcasting, for a total time of 11x10^-6 s.

We will get minimized time when all computers keep repeating the message to another which is still ignorant of it, once the message reach them

Are you sure we can't do better than this? Why isn't there a better algorithm than this?

Pi Han Goh - 4 years, 3 months ago

Broadcasting a message in a fully connected network

2 solutions

0 pending reports