Broken Ring Attraction
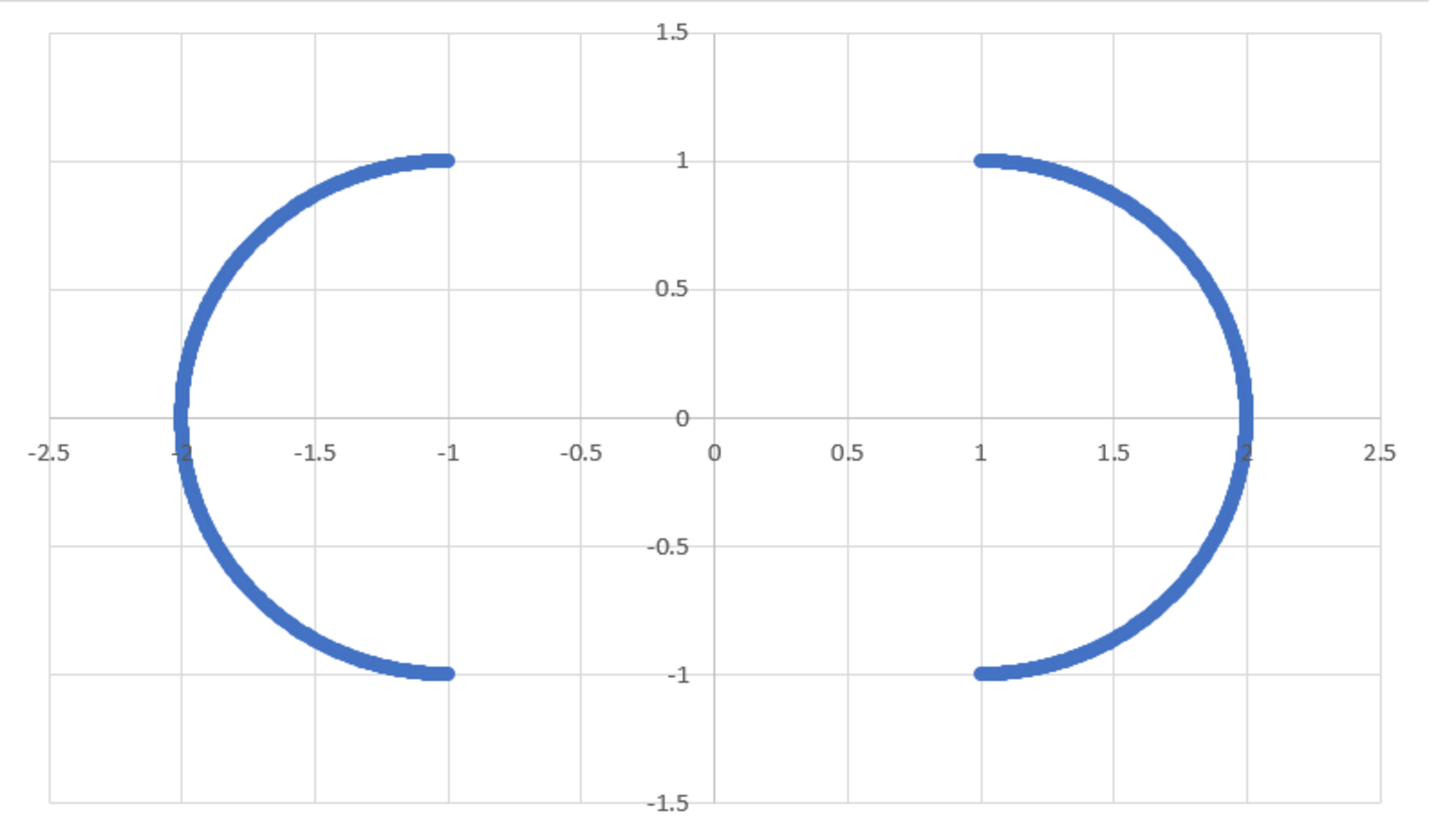
A uniform circular ring of radius has unit of mass per unit length.
The ring is initially centered on the origin. Then it is broken and the right half is moved distance unit to the right, and the left half is moved distance unit to the left.
What is the magnitude of the gravitational force between the two halves?
Note: Universal gravitational constant , for simplicity
The answer is 0.8386.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Arbitrary points on the right half and left half of the ring are:
r 1 = ( 1 + cos θ 1 ) i ^ + sin θ 1 j ^ ∣ r 2 = − ( 1 + cos θ 2 ) i ^ − sin θ 2 j ^
The gravitational force between arc length elements on each half is (According to the law of gravitation, considering unit radius and unit mass per unit length):
d F = ( ∣ r 1 − r 2 ∣ 3 G d θ 1 d θ 2 ) ( r 1 − r 2 )
Substituting expressions and recognising by virtue of symmetry that the net y-component is zero, the net magnitude of the force in the x-direction is:
F x = ∫ − 2 π 2 π ∫ − 2 π 2 π ( ( 2 + cos θ 1 + cos θ 2 ) 2 + ( sin θ 1 + sin θ 2 ) 2 ) 3 / 2 ( 2 + cos θ 1 + cos θ 2 ) d θ 1 d θ 2 ≈ 0 . 8 3 7 4
I used Wolfram-Alpha to get the answer to the double integral. This is slightly different from the mentioned answer of 0.8386.