Build a square from squares?
Can you use all of the pieces to build a large square? And if possible, what is its side length?
- one 6 × 6 square
- two 5 × 5 squares
- three 4 × 4 squares
- four 3 × 3 squares
- five 2 × 2 squares
- six 1 × 1 squares
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Moderator note:
Nice job producing an actual example of the larger square being made! It's very tempting on this problem to just produce what the answer would be if the square configuration worked, but there is no guarantee here that the configuration even exists so a complete answer needs to produce one.
Making this kind of configuration in general is considered a hard problem and has no easy algorithm or method.
Thanks for showing that we could place these squares together to get a larger square!
Sometimes, it can't be done, even though the areas are equal. E.g Even though 8 2 + 8 2 + 8 2 + 2 2 = 1 9 6 , clearly we can't use 3 8 × 8 squares and 1 2 × 2 square to form a 1 4 × 1 4 square.
Log in to reply
Calvin, this is actually a real interesting problem, as 1) it is not trivial (i.e., there is no identity here), and 2) there's an infinity of of cases similar to this, where a sequence of squares done like this that adds up to one large one with integer sides. But is there any other instance where can they be packed like how Profe did it? Hmm...
Yes, the easy part is determining what size square it will make if it's possible. The hard part is coming up with a good way of finding a solution, or proving that no solution exists.
In principle, you can run a backtracking algorithm. Think of the target square as divided into 196 cells, and at each step locate the first unfilled cell in line-by-line order, and place the largest square you have available that will fit with that cell as its upper-left corner. If you have to backtrack, then place a square of the next size down from the one you placed there before.
In this case, it just so happens that this algorithm produces a solution first time, without any backtracking! But in the general case it wouldn't, and there must be a better way of doing it.
Log in to reply
There isn't. If the problem is NP-complete we can't do it efficiently. We can try with heuristics, but then there's no guarantee we'll find the solution in a short enough time.
I wonder if there are other ways to build the square, or is it unique?
P/S: the solution will look better if you LaTeX it.
Log in to reply
See my comment to Calvin, but to answer your question about packing these squares, I don't know.
Log in to reply
I've edited the options to allow for "not possible".
I think this makes the question really interesting!
Log in to reply
@Calvin Lin – Yes Sir, That made the question a lot more difficult. Is there any method of finding if the squares would actually make up a bigger square or not? Thanks
Well there are, at least, some slight alterations of the arrangement already given. For example, the two "9" squares on the top row (or just the left one of them) could be moved two units to the left, with an appropriate rearrangement of "4" and "1" squares.
Assuming geometric configuration exists. Ans= +Sq. Rt. [Sum of (7-i)i^2for i=1 to i=6] +Sq Rt 196= 14
Log in to reply
Right. The important part is proving whether such a configuration exists...
Log in to reply
Though this is a more interesting problem, this problem here reads. "If you use all of the pieces to build a large square ...", so it implicitely states that a fitting configuration does exist. Otherwise text should have read "Can you use ..., and if possible, what is its side length?"
Log in to reply
@Martin Ramsch – There is one option that reads "Not possible", so maybe this configuration is impossible?
Log in to reply
@Pi Han Goh – True, overlooked that. Then problem text is inconsistent, because "If you use ..." then is misleading. Thanks for your comment!
Log in to reply
@Martin Ramsch – Hmmm, in that case, how do you propose to improve the problem statement?
Log in to reply
@Pi Han Goh – As I already did above: "Can you use ..., and if possible, what is its side length?"
Log in to reply
@Martin Ramsch – Oh, I overlooked that too! Haha. I've edited it. Thanks for helping out :)
Very good problem!
I dont get it...so if we want to solve this problem then the only way to do it is to make it,like, practically???
Log in to reply
Yeah, there's no (general) shortcut to figure out if there's an actual geometric configuration that exist.
@CalvinLi please tell me if this is the only way to solve this problem
All you had to do was add the areas to make a square. so length times length equals area of square. and area is 196 and square root it to get 14. Thanks for the problem!
Log in to reply
How do you know that such a configuration is possible? Maybe the answer could still be "Not possible"?
I disagree with the moderator note. Its not hard to conclude with Calvin's example that it's impossible because 8+8=16 so there's no way to make a 14 long face with 8x8 squares. However, constructing such a square from the given pieces is a simple matter of constructing the border from the given square lengths and filling in the gaps with remaining pieces. You can determine quickly if the side lengths of the given tiles can possibly construct the squares border. It's also readily apparent that the "filling" portion will be easier with smaller pieces. Notice that the large squares are on the exterior. I actually (by chance, because there are many more than one ways to do this), constructed a congruent tiling (flipped vertically though). Even if there's no rigorous method to solve 100% of the time, that doesn't mean in general this is hard.
I love being proven wrong about stuff though.
Throw me a "hard" one with square tiles and put it in the advanced section. I challenge you.
Log in to reply
Please note that the note says "Making this kind of configuration in general ". IE we're not talking about the specific case as given, but about the general problems where you are given a i copies of squares of side length b i , whose area sums to S 2 , then can we indeed form a square of side length S ?
Even if there's no rigorous method to solve 100% of the time, that doesn't mean in general this is hard.
I disagree. If there is no rigorous method to solve this 100% of the time, then it means that for infinitely many cases you are reduced to case-by-case checking, and thus the problem is indeed hard (with a loose definition of what it means).
Just have a look at this and then you'll get to know just how hard this kind of problem is. It took years to get an algorithm to find the g e n e r a l solution to this problem. And the way it was found is just beautiful. Things that seem easy sometimes turn out to be really hard you know.
Log in to reply
Wow, that's a great presentation. I wonder if that 1²+2²+3²+...+24²=70² is at all possible, or has it ever been proven to be impossible. :-)
Log in to reply
@C . – Yeah I have wondered about that too. I really want a solution for that.
Why can't I think like this?
Log in to reply
Check out the Outside the Box Geometry course that helps to guide you in understanding how to apply the concepts and relate them to each other.
Where's the example that "Moderator" congratulated you on? :-s
Edit: somehow i wasn't able to see the image on the right before... now i can. To prevent this from happening again, the image is https://ds055uzetaobb.cloudfront.net/image_optimizer/69385b7ceae544190a47f7ff7c5c8bdad011d9e0.png
Simple answer calculate the total area of all the squares and root it to find √196 =14 . Since ALL the squares have to be used as specified in the question
No, this is not always true. Read up Calvin's comment under Profe Ronald's solution.
One simple way to solve this is sum all the side lengths of the small squares.
6+ 5 ∗ 2 + 4 ∗ 3 + 3 ∗ 4 + 2 ∗ 5 + 1 ∗ 6 = 56
Now you have a perimeter of the large square. Dividing perimeter with 4 gives us the side lenght
4 5 6 =14
answer is 14
It is a coincidence that the sum of the side lengths of the squares turned out to be the perimeter of the big square. This does not always hold true. In fact, it rarely holds true.
We can make a 3 × 3 square from one 2 × 2 square and five 1 × 1 square. The sum of their side lengths is 7, while the perimeter of the 3 × 3 square is 12.
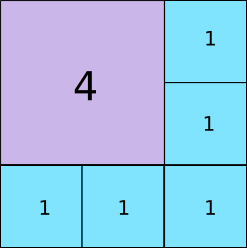
Log in to reply
I'm not understanding what you mean by the sum of their side lengths is 7? I feel like the above solution still works for your example. The side lengths are 3..the perimeter is 12...12/4 is 3.
Log in to reply
By sum of side lengths, I mean adding all the side lengths of the small squares. In this case, it is 2 + 1 + 1 + 1 + 1 + 1 = 7. The perimeter of the big square is 3 × 4 = 1 2 .
This quiz from the beginning has provided an important clue is: "all SQUARES perfectly formed a large SQUARE".
So, we do not need to imagine the impact all areas of greatest to least because it would establish a large SQUARES perfectly.
We are fairly calculate the total area of all of these SQUARES and then look for the roots of its value, so we found the side of a large SQUARE that is formed from all the SQUARES provided in this quiz.
So, S = [(6 x 6) + 2 x (5 x 5) + 3 x (4 x 4) + 4 x (3 x 3) + 5 x (2 x 2) + 6 x (1 x 1)] ^ (0.5) S = 196 ^ 0.5 S = 14
This does not guarantee that we can form the 1 4 × 1 4 square, even though the total area of the given squares is equal to the area of a 1 4 × 1 4 square, See Calvin's comment in Profe Ronald's solution for a counterexample.
Log in to reply
It says "IF", so etiher the question is wrong or you can use the non-constructive method.
Please..., pay attention for selection of sentences in my comment. "This quiz from the beginning has provided an important clue is: "all SQUARES perfectly formed a large SQUARE" for a part of proposed problem: "If you use all of the pieces to build a large square, what is its side length?"
Answer is 14 :
- (6^2)×1 = 36
- (5^2)×2 = 50
- (4^2)×3 = 48
- (3^2)×4 = 36
- (2^2)×5 = 20
- (1^2)×6 = 6
So 36+50+48+36+20+6 = 196
196 = 14 ^2
The answer is 14.
Is it true that the squares can actually be arranged to form a larger square? Does this always happen when the areas add up?
Log in to reply
This is an interesting problem (and NP-complete), but not the problem given.
- Sum up the area of all squares then see if it can be the product of a number and it self (x^x)because the area of a square = x^x(x is the side length of the square)
So:
one 6x6 square= 36cm2 two 5x5 squares=50cm2 three 4x4 squares=48cm2 four 3x3 squares=36cm2 five 2x2 squares=20cm2 six 1x1 squares=6cm2
Sum up: 36 + 50 + 48 + 36 + 20 + 6 = 196cm2 = 14cm x 14cm
=> The side length is 14 cm
This method does not show that we can build a large square out of these squares. See Calvin's comment on Profe's solution.
Log in to reply
I haven't seen your comment about the solution
Log in to reply
I mean Calvin's solution, not mine.
Log in to reply
@Christopher Boo – He is right though but only in some situations
Add all the areas of the squares
6×6=36
Now we shall multiply the number of squares with the following area
5×5×2=50
4×4×3=48
3×3×4=36
2×2×5=20
1×1×6=6
Now we add the areas 36+50+48+36+20+6=196 Now a^2=196 a=14
This does not guarantee that we can form the 1 4 × 1 4 square, even though the total area of the given squares is equal to the area of a 1 4 × 1 4 square, See Calvin's comment in Profe Ronald's solution for a counterexample.
I added the area of all the squares together, then rooted the result to find the side lengths. - 196 is the area of all squares added. - square root of 196 is 14.
This is why this problem has more apparent solvers than actual solvers. To get the number 14 is easy. But to actually solve the problem, you need to eliminate the alternative of it not having any solution. And that can only be done by constructing the actual square, which is likely not to be the same as the example in the solution above.
Answer is 14.
6 x 6 = 3 6
5 x 5 = 2 5 >>>> 2 5 x 2 = 5 0
4 x 4 = 1 6 >>>> 1 6 x 3 = 4 8 ;
3 x 3 = 9 >>>> 9 x 4 = 3 6 ;
2 x 2 = 4 >>>> 4 x 5 = 2 0 ;
1 x 1 = 1 >>>> 1 x 6 = 6 ;
3 6 + 5 0 + 4 8 + 3 6 + 2 0 + 6 = 1 9 6 = 1 4 2
Then side of the square 1 4 .