Bumbling to Honey
 Bombus the BumbleBee wants to get to the cell containing honey.
Bombus the BumbleBee wants to get to the cell containing honey.
Each time, he can only take a step to a neighboring cell, that moves him to the right.
How many ways does he have of reaching the honey in the last cell?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Why Fibonacci
Let the number of ways to get to the n th leftmost hexagon be F n . Thus, we want to find the value of F 1 2 .
Note that F 1 = 1 . Also, F 2 = 1 . Now, to get to F 3 , Bombus can arrive through F 1 or F 2 . Thus, F 3 = F 1 + F 2 = 2 .
In general, to arrive on F n Bombus can choose either to arrive from F n − 1 or F n − 2 . Thus F n = F n − 1 + F n − 2
But this is a sequence we recognize: the Fibonacci sequence!
We can then apply the Fibonacci recursion to get that F 1 2 = 1 4 4 .
Nice solution, Daniel. Follow-up question: If we added a row of six cells above the two existing rows, and had Bombus start at the top left cell with the same rules of motion, how many ways would he have of reaching the lower right cell? I'm not sure if there is a "pretty" answer to this version.
Log in to reply
That would be an excellent question to post! I was contemplating doing so, but haven't had the time write it out. We would have a two sequence linear recurrence relation to solve.
In this problem, if A i is the number of moves to the ith hexagon in the top row and B i is the number of moves to the ith hexagon in the bottom row, then we want to solve
A n = A n − 1 + B n − 1 , B n = A n + B n − 1 , A 1 = 1 , B 1 = 1
In all likelihood there is not a very nice answer (after all, if you think about it, calculating the Fibonacci numbers isn't very nice either).
I calculated that if there are n columns and 3 rows like you proposed, then the number of ways to get to the end is 1 2 ( 3 + 3 ) ( 2 + 3 ) n + ( 3 − 3 ) ( 2 − 3 ) n − 6
There is a simple way to solve that, in fact, or at least a visualization:
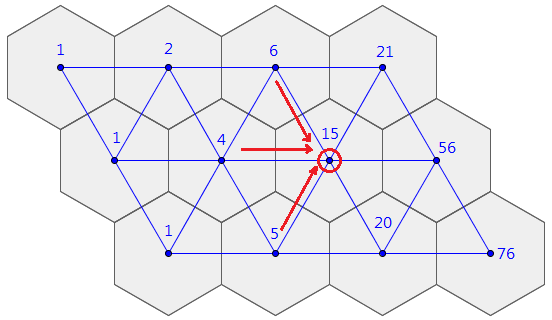
For each cell, it can only be reached from its neighbors to the left. (For example, the marked 15 hex can be reached from the top-left (6 ways there), from the left (4 ways there), and from the bottom-left (5 ways there); just add up all of them. Thus by carefully evaluating each cell from the leftmost to rightmost, we can find the answer.
Hmmmm this problem looks familiar .
Can we use C or P to find the answer , I mean Combination etc
Log in to reply
Not in a direct way.
There is an indirect way of doing so, which highlights why the answer is the Fibonacci sequence.
U say that to get to F2 there is one way . But why is that because i can reach F2 in two ways -One is directly from bee's position ,And the other is from is from F1 .As im not breaking the rule coz im still moving to the right from F1>F2. Moreover it is no where stated that we need to find the shortest path
Log in to reply
You are talking about F 3 .
F 1 is the bee's starting position.
Log in to reply
oh! ok...ok...Sorry i misunderstood............Well,Good solution then.But did u check that the sequence Fn=F(n-1)+F(n-2) continues all through upto the end position?
Log in to reply
@Saaket Sharma – It is symmetric, so it holds.
can you please explain the fibonacci sequence or get me a link to that? i am only known to permutations and combinations.