But There Would Be No Mass!
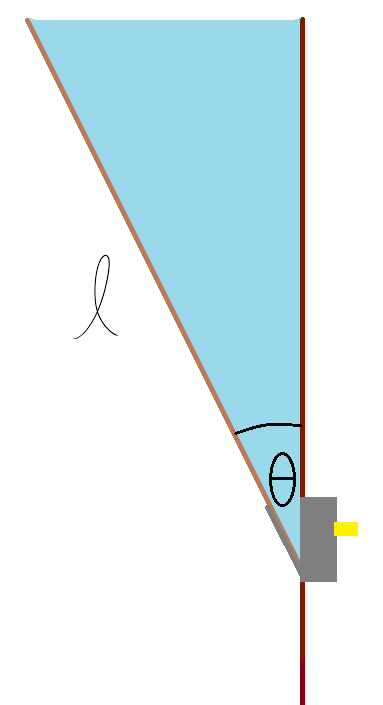
In a two-dimensional setting, a water-filled tub of length ℓ can be formed by attaching a platform of negligible mass and width to a wall. Using a lever, one can change the angle of elevation, θ , between this platform and the wall.
If the water always levels out at the very top of the tub, find the limit of the tub's center of mass as the angle of elevation increases to approach 9 0 ∘ . Write your answer as the horizontal distance from the platform's pivot to the center of mass in terms of ℓ .
Assume that the water is of uniform density.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The water tube always forms a triangle with one vertex being the pivot point. We know that the distance from any vertex to the center of mass in a triangle is 2 / 3 of the median line. Consider the point where the median line from the leftmost point of the triangle intersects the wall and call it P . This point will have distance 1 / 3 of the median line to the center of the mass. As the angle tends to 9 0 ∘ the triangle looks more and more like a straight line and therefore the median line tends to the length l and the point P tends to be the same as the pivot point. Therefore, the solution is 3 ℓ ..
This might not be the most elegant solution. Also sorry for the formatting, I'm on my phone.
What do you want to update your name to?
I was thinking that as the angle between the platform and the wall approaches 90 degrees, the "pool" would turn into a straight line of an infinitesimal amount of water thus the center of mass would be length/2... where did I go wrong?
Log in to reply
Well, what Aaa Bbb said is actually pretty accurate. I never thought of it that way, since I was thinking about it using Physics, rather than Geometry.
Jake, note that, even under an infinitesimal amount of water, the infinitesimal angle of elevation between the platform and the horizontal would still create a triangle-shaped pool of water. Thus, as one goes further from the pivot point, the water in that location would approach the infinitesimal quicker than water closer to the pivot. However, I am about to post a more mathematically-sound solution.
Log in to reply
I should really chance my name.. :-) Nice solution btw. I knew there had to be a more scientific one than mine.
Log in to reply
@Kai Ott – Thank you! :D I enjoyed your solution as well, because it's simpler and allows one to better visualize the problem in real life. Your name is fine; I did not think much of it.
As θ approaches 2 π , the length of the median (i.e. the line joining the center of the platform and the opposite vertex) tends to l (you can draw this). Since we know that the centroid (center of mass) is divided in the ratio 2 : 3 with the side being bisected (platform) being closer to it, the answer is 3 l .
Relevant wiki: Moment of Inertia
First of all, since the pool of water can be modeled as the area between the x -axis and a function, f ( x ) , one can flip the model on its side as so: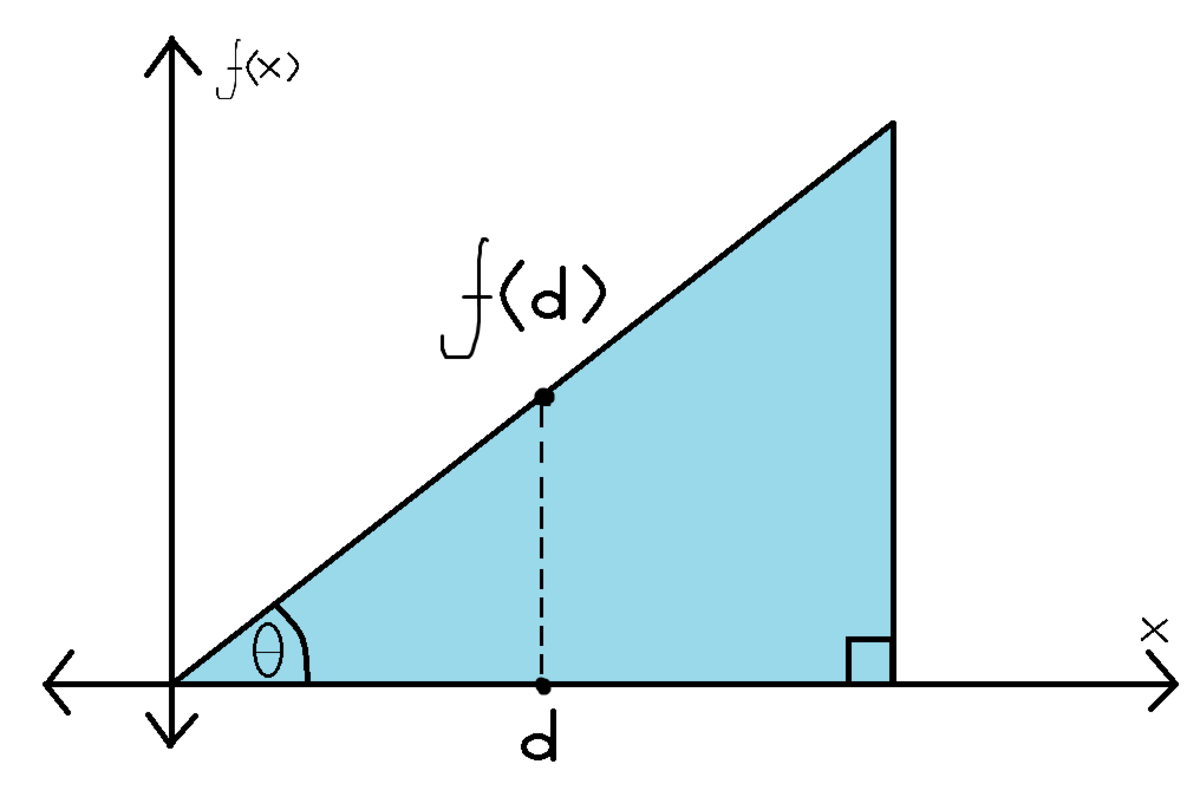 In this case, the center of mass we are looking for is the
y
-coordinate
of the center of mass, since in the original model, this would be along the horizontal. The formula for this is
Y
cm
=
∫
d
m
∫
y
d
m
.
In this case, the center of mass we are looking for is the
y
-coordinate
of the center of mass, since in the original model, this would be along the horizontal. The formula for this is
Y
cm
=
∫
d
m
∫
y
d
m
.
For this two-dimensional setting, ρ = A M , where ρ is density, M is total mass, and A is total area. Writing this in differential form, ρ = d a d m , and this can be solved for d m : ρ d a = d m . Substituting d m into the center of mass formula (and noting that the water is of uniform density, so ρ can be factored out), we get the following: ∫ ρ d a ∫ y ρ d a = ρ ∫ d a ρ ∫ y d a = ∫ d a ∫ y d a From here, since the water is level with the top of the tub, the area under f ( x ) makes a right triangle. Thus, tan θ = x f ( x ) = s l o p e when x > 0 , and rearranging this equation, y = f ( x ) = ( tan θ ) x .
Going back to our modified center of mass equation, since d a = d x d y , we can further rewrite this equation by using a double integral and solving it: ∫ d a ∫ y d a = ∬ 0 f ( x ) d y d x ∬ 0 f ( x ) y d y d x = ∫ f ( x ) d x ∫ 2 1 ( f ( x ) ) 2 d x Plugging in the necessary variables (and noting that tan θ does not depend on x and, therefore, can be factored out), we can solve: ∫ 0 L f ( x ) d x ∫ 0 L 2 1 ( f ( x ) ) 2 d x = ∫ 0 L ( tan θ ) x d x ∫ 0 L ( 2 1 tan 2 θ ) x 2 d x = tan θ ∫ 0 L x d x 2 1 tan 2 θ ∫ 0 L x 2 d x = 2 tan θ ( 2 1 L 2 ) ( 3 1 L 3 ) = 3 L tan θ By this point, one might be inclined to say that the center of mass would be infinitely far from the pivot, since lim θ → 9 0 ° − tan θ = ∞ . But once one views the model again, we can easily see that the length between the pivot and the top of the water, L , will also tend to 0 as θ approaches 9 0 ° .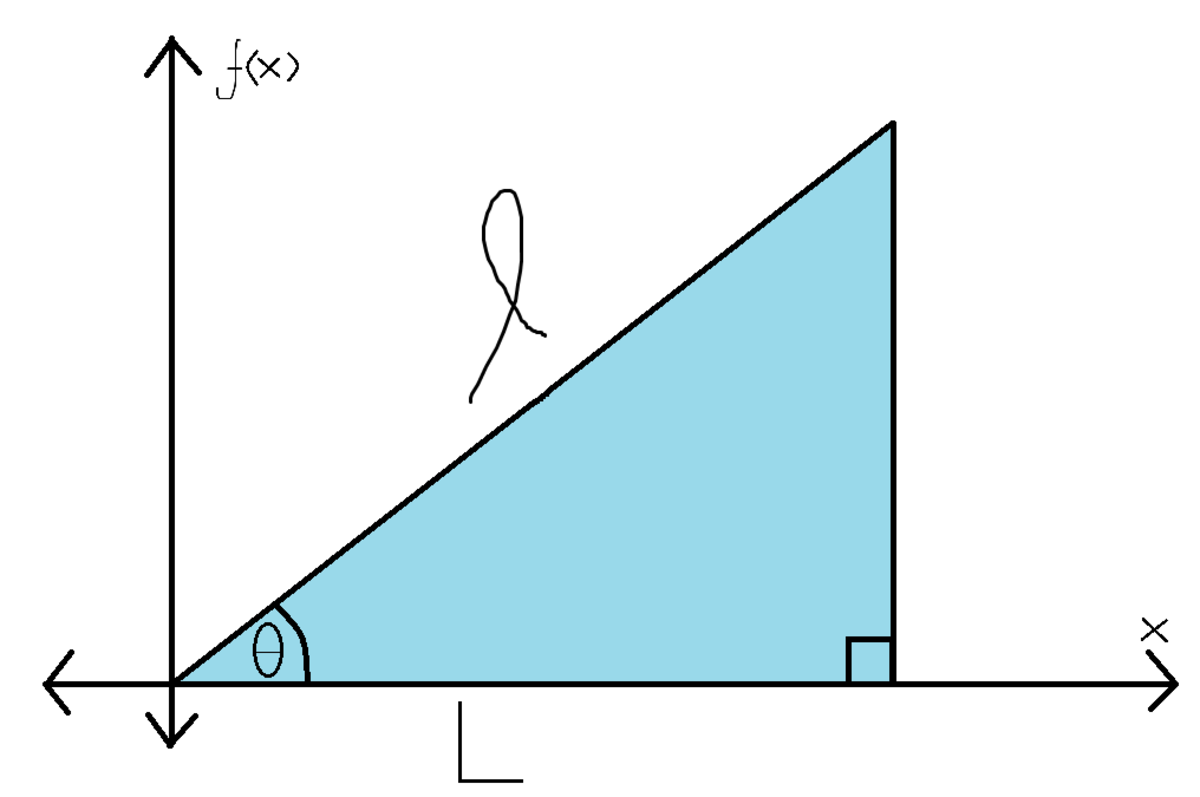 Therefore, since
lim
θ
→
9
0
°
−
3
L
tan
θ
=
3
(
0
)
(
∞
)
, we have an ambiguous case. However, this problem is not over yet. Since the area under
f
(
x
)
makes a right triangle, we can define another property of this triangle to get rid of the singularity:
cos
θ
=
ℓ
L
. By rearranging this relation to solve for
L
, we get
L
=
ℓ
cos
θ
, which can be substituted back into
3
L
tan
θ
to simplify it:
3
L
tan
θ
=
3
(
ℓ
cos
θ
)
(
cos
θ
sin
θ
)
=
3
ℓ
sin
θ
The limit of
sin
θ
at
9
0
°
is defined, so the limit at
9
0
°
of the distance to the center of mass is
θ
→
9
0
°
lim
3
ℓ
sin
θ
=
3
ℓ
Therefore, since
lim
θ
→
9
0
°
−
3
L
tan
θ
=
3
(
0
)
(
∞
)
, we have an ambiguous case. However, this problem is not over yet. Since the area under
f
(
x
)
makes a right triangle, we can define another property of this triangle to get rid of the singularity:
cos
θ
=
ℓ
L
. By rearranging this relation to solve for
L
, we get
L
=
ℓ
cos
θ
, which can be substituted back into
3
L
tan
θ
to simplify it:
3
L
tan
θ
=
3
(
ℓ
cos
θ
)
(
cos
θ
sin
θ
)
=
3
ℓ
sin
θ
The limit of
sin
θ
at
9
0
°
is defined, so the limit at
9
0
°
of the distance to the center of mass is
θ
→
9
0
°
lim
3
ℓ
sin
θ
=
3
ℓ