C Blank Cards
There are two cards—one with the letter "C" and the other blank.
You want to check if the following statement is true for the two cards:
If a card has a number on one side, then it is blank on the other.
Which card(s) must you flip?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Moderator note:
There have been many arguments raised in the comments, far too many to address in a single note; if you are having issues understanding this problem I certainly recommend checking those first (and some of the other solutions).
One primary source of confusion seems to be equating
If a card has a number on one side, then it is blank on the other.
with
If a card has is blank on one side, then it has a number on the other.
These are very different! The second is called the converse of the first. With the original statement, a card being blank on one side and having something other than a number on the other side is irrelevant.
What if the blank card doesn’t have number on the back
Log in to reply
Then there is no problem at all - the if-then statement doesn't trigger in the first place.
Here's a different version: "If you are under 30, you must pay an extra $50 on your car insurance." If someone is not under 30, that doesn't make the statement false just because they didn't pay the extra $50! It only applies to people under 30.
Log in to reply
What if on the other side of the C card there is a flower...you have found o evidence to support the truth of what lies on the opposite side of a numbered card.
Log in to reply
@Jerry Duncan – You seem to be worrying about the scenario where there is no number on either card. That's no problem at all. We just want to enforce the condition "IF there is a number on one side, THEN it is blank on the other." If we have no numbers, the if-then statement is true.
This is known as "vacuously true" and can be counterintuitive, but definitely matches real-life use. This was what I tried to bring up with my insurance analogy. You can also try out Agnishom's:
If a person is under 18 years, then they should not be drinking.
If there's nobody at a party under 18 years, then the rule is all clear! This is analogous to there being no number on either card.
You're mixing the if-then interpretation up with an AND statement. "It is the case that a card has a number on one side and a blank on the other" is a much different scenario than "If a card has a number on one side then it has a blank on the other."
Both cards could be complete different andere therefor i would check Them Both.
Log in to reply
If the opposite of the blank side is a number, the statement is true. If the opposite of the blank side is anything else, the statement is still true - the if-then statement doesn't trigger in the first place.
Log in to reply
And what if the other side of time card is... a picture of a flower. The problem needs some premises/parameters/limitations established at the very beginning.
Log in to reply
@A Former Brilliant Member – There is no problem then.
The statement is false if and only if you have a card that
has a number on one side
and is not blank on the other side.
This can only happen with the first card.
If the second card has a flower on the opposite side, the statement is still true, because the statement doesn't even apply to the second card.
It's like if you made a statement that applied only to people aged 40 and older. You don't need to check people who are younger than 40! They aren't relevant to the truth or falsity of the statement.
@Blan Morrison, your solution is wrong. The problem, as stated, requires that you check "if the statement IS true". Correct answer for me is that both of them should be flipped, and this is why: 1. Flip blank card
a. If it has number, go to 2. It still may be that not all cards with a number are blank. Possible solutions: False or true, but in any case determinable!
b. If it has anything else, go to 2. At this point, the statement might be false or indeterminable, but not true.
2Flip the C card
a. If it has a number, the statement is false, whatever the solution for 1 was.
b. If it has anything else,
and solution for 1 was a, the statement is true.
and solution for 1 was b, you cannot determine if the statement is true or false, hence it is indeterminable.
Log in to reply
There is no way whatsoever for the blank card to falsify the original statement, because the if-then statement can only be true if the first part (the hypothesis) is true. If the hypothesis is in fact true (and there is a number on one side) then we already know the blank is on the other! If it's something other than a blank, than you never need to worry about the second part of the if-then statement.
Regarding not caring if the other side of the blank card is something other than a number, here's a different version: "If you are under 30, you must pay an extra $50 on your car insurance." If someone is not under 30, that doesn't make the statement false just because they didn't pay the extra $50! It only applies to people under 30.
If neither card has a number on it, the statement is considered to be "vacuously true" in the world of logic.
Log in to reply
But you are asked to check if the statement IS true. Realizing that nothing contradicts the statement, doesn't prove it right. Your point from the beginning is neutral, you are checking if the facts prove or disprove your statement.
Log in to reply
@Branislav Milutinovic – Yes, if statement is not false, it must be true. The statement only applies to the two cards shown. So if we have checked both of them, we have entirely confirmed the statement must be true.
It's like a room where we check "if anyone in this room is under 18, they have parental permission." We check every person in the room, and all of them are over 18. Then we have proven the statement is true, even though nobody has a chance to make the statement false.
It becomes a question of semantics I think. If I want to check if the statement is true I need to check both. If I check the first card and it is blank, the other one can have a number or be blank. I can't know if the statement is true or not until I check the other one.
It's a poorly worded problem.
Log in to reply
No semantics here - it doesn't matter what's on the other side of the second card at all. If the other side happens to be a number, the statement is true. If it's something else, it doesn't matter at all what it is, because the "if-then" statement never got triggered in the first place. If-then statements only apply when their hypothesis (the first part) is true.
In order to prove that a statement is true, you must prove that it's not false, otherwise it's just confirmation bias.
It is not poorly worded. I posted a solution with a picture that may help you understand why you only have to check one.
The problem was to check if the statement was true, not false.
Flip card C could prove:
number - statement false;
blank or letter - proves nothing.
Whereas flip blank card could prove:
number - statement true;
blank or letter - proves nothing.
Hence, to check if statement is true, only check blank card.
Log in to reply
Consider the problem with just the blank card.
Then the statement is true no matter what is on the opposite side of the blank card . The statement is true already given the information you have. Therefore you do not need to check anything.
Now consider the problem with just the C card.
Then the problem can either be true or false. So you need to check the card in that case.
Log in to reply
"Then the statement is true no matter what is on the opposite side of the blank card. The statement is true already given the information you have. Therefore you do not need to check anything."
No.
If the blank card is flipped, and there is a smiley face than the statement is false for both.
The C card can never be true because C is a character not an integer.
The only case where "If a card has a number on one side, then it is blank on the other." is if the blank card has a number on the other side.
Log in to reply
@James Hemmaplardh – I'm trying to suss out your misconception here. First note
If a card has a number on one side, then it is blank on the other.
Does not mean
If a card is blank on one side, it has a number on the other.
That's called the "converse" and is a different statement. Many statements are true where the converse is not true. ( compare "If I am in Paris, then I am in France" vs. "If I am France, then I am in Paris.)
So the only thing we need to look at is situations where a card has a number on one side. Since we don't see any numbers, the thing that could cause the statement to be false instead of true is if you have a number on one side and something not blank on the other.
You state "The C card can never be true because C is a character not an integer."
If the C card has a number on the opposite side, then you have a case with a number on one side and not-blank on the other, so the statement is false for that card. However, if the C has anything else on the other side, then the statement is true for that card - we don't have to worry about the "number trigger" in the first place.
This is known as "vacuously true" - we make an if-then scenario that is true simply because the "if" part never happens. The warning "If you drink this poison, you will die" doesn't become false just because everyone declined to drink the poison - it just means the hypothesis never happened.
You seem to be interpreting an if-then statement more like an AND statement - "it is true that there is a card with a blank on one side AND a number on the other." That is much different then an if-then statement. If-then means IF the first condition happens THEN the second condition happens - not that they both, necessarily must happen.
Log in to reply
@Jason Dyer
–
Yes Jason, I was seeing the "If a card has a number on one side, then it is blank on the other." as an assertion where to prove it false I must prove it is true in any case, not an if case.
I see that the only way to prove the assertion is by finding a true negative where a card has a number and is not blank.
Thanks for the detailed explanation.
The statement is if it has a number on one side it will be blank on the other. It clearly asks if the statement is true. If the other side of the blank card is blank it is false. The c card even if it is blank on the other side is still false because a letter is not a number. Hence you can gain information useful to the task of determining if the statement is true only by flipping the blank card.
Log in to reply
If the other side of the blank card is blank then the statement is not false. For the statement to be false you have to falsify:
If a card has a number on one side, then it is blank on the other.
not
If a card is blank on one side, it has a number on the other.
The second statement is the converse and it is not equivalent. Compare
If a number is even, it is an integer.
with
If a number is an integer, it is even.
In mathematics, that means if we want to use a statement both directions, we have to prove it both directions first; we can't assume.
Log in to reply
The statements says: all cards that have a number on one side are blank on the other. There are 6 possibilities: 1) Number-blank 2) Number-anything else 3) Number-number 4) Blank-blank 5) Blank-anything else 6) Anything else-anything else. The left card can be in state 2, 5 or 6 and the right one 1, 4 or 5. Turning only the left card proves the statement wrong only if we find a number on the other side, situation 2. In other cases (5 and 6) we cannot say anything about the statement. If we turn only the right card we cannot say anything about the statement. For e.g. we find a number and the statememt seems true but it becomes false if the left card has a number on the other side. So I think we have to turn both cards.
Log in to reply
@A Former Brilliant Member – You seem to be interpreting the if-then as an AND statement instead. "A card has a number on one side and a blank on the other side" is much different than "if a card as a number on one side, it has a blank on the other". IF means that the first condition has to be true for the statement to even possibly be false.
Considering the blank card's situations
blank and blank --> no worries here, you don't have a number that might make the if-then statement false
blank and number --> it has a number on one side, but it's blank on the other side, so we're still in the clear
blank and something else --> again, no worries here, you don't have a number that might make the if-then statement false
If the only statement we are given is that if there is a number on one side the other side is blank...then if anything other than a number is on the back of the blank card we have proved nothing. If there is anything other than a number on the back of the card with a C we still have proved nothing. If the statement exists such that the only thing whose opposite side is blank is a number then we only need to flip the blank card to see if it is true. Just because there is no number on the back of the lettered card doesnt mean a numbered card will have a blank.
Log in to reply
"Just because there is no number on the back of the lettered card doesnt mean a numbered card will have a blank." Indeed, it may be the case there is no number at all. In such a case, "If a card has a number on one side, then it is blank on the other." is true. It's known as "vacuously true" because there's no numbers to worry about in the first place.
Compare with Agnishom's analogy answer: we want to make sure "If a person is under 18 years, then they should not be drinking." Suppose everyone at the party is over 18 years old. Then the party is all clear - there's no way to make the statement false with an underage drinker.
Log in to reply
- there's no way to make the statement false with an underage drinker.
Be careful that this part of your sentence is not taken out of context. It lacks a qualifier.
there's no way to make the statement false with an underage drinker, because nobody is underage.
But, I believe that the analogy Agnishom was making is that if people aren't drinking (blank), there's no need to check their age (number).
c is a number. The other side needs to be blank.
c is the Roman numeral for 100. It's also the speed of light.
You do not need to check either cards because the question is whether the statement is true for BOTH cards. One card clearly has a letter and not a number or blank on one side, and therefore the statement is already false. You can argue semantics about whether C is a number but then the question is poorly defined.
Log in to reply
A conditional statement (if, then) is only false when the antecedent (the condition of the 'if') is true and the consequent (the rule stipulated by the 'then') is false.
Here's an example:
Statement: " If it is raining, then I will stay at home. "
| Case | (Antecedent) Raining | (Consequent) Stay at home | Result |
| 1 | Yes | Yes | T r u e |
| 2 | Yes | No | F a l s e |
| 3 | No | Yes | T r u e |
| 4 | No | No | T r u e |
The statement is true until I break the rule by going out when it is raining.
- If it's raining, and I stay at home; I have not broken the rule - The statement is true.
- If it's raining, and I go out; I have broken the rule - The statement is false.
- If it's not raining, and I stay at home; I have not broken the rule - The statement is true.
- If it's not raining, and I go out; I have not broken the rule - It remains a true statement.
Neither of the faces presented in the problem's scenario have the condition of the antecedent (they are not numbers), so we determine that they are the consequent.
Considering that a blank face always results in the statement being true (cases 1 and 3 in the table above), we gain no further sense of truth by turning the blank face.
The only consequent that has the potential to cause the statement to be false is a non-blank face.
- If the face on the other side of C is a number , the statement is false.
- If the face on the other side of C is anything else , the statement is true.
As the only card that can determine the truth of the statement in the problem, we must turn C. And only C.
Log in to reply
Great explanation! Although too late to make it up the rankings why not post it as a solution?
Log in to reply
@Robert Williams – I have literally just done that. Haha!
As I pointed out in my posting, you are using false premisses and your example is not representing the original problem.
In 3... the statement is true, is only correct if you have a single incident of weather/stay-home. It is as if you use the given original problem, but reduce it to a single card problem.
"As the only card that can determine the truth of the statement in the problem, we must turn C. And only C."
This is a false conclusion, because for all cases where your statement according to 1-4 is resulting a true, does not determine the outcome of the second card. The second card can still be one of the following combinations:
Blank - Blank Blank - C Blank - Number
The reason that Blank-Blank and Blank-C must be allowed is because these combinations are not excluded in the problem outline.
Log in to reply
@Flex Domino – Blank-Blank, Blank-C, and Blank-Number all result in the conditional statement being true.
A conditional statement is false when (and only when) the Antecedent is true and the Consequent is false.
When considering Blank as an Antecedent, this means that the Antecedent condition is false - Which results in the conditional statement always being true. When considering Blank as a Consequent, this means that the Consequent is true. - which results in the conditional statement always being true.
When Blank is on any side of a card, the result is always true. Which is why we don't need to check it.
Card C and card Blank form a combination where both cards must be true for the statement to be true for
both
cards.
If you already know that the Blank card always results in true, why do you want to check it?
Flipping the C card only tells you if the statement is false. You need to flip the blank one, AND get a number to know it's true. So really, there just isn't enough information.
Log in to reply
Checking the blank card confirms something that we already know about this material conditional statement - The statement is true for the blank card, regardless of what is on the other side.
Only when you have eliminated the possibility of falsities existing can you determine that something is true.
This can only be done by checking the card with C.
the card showing blank could easily have a letter on the other side. the card showing 'c' could have a number of items on the other side.
there's some false premise happening here.
Log in to reply
Yes, the C could have many different things on the other side. We need to check it just in case there's a number on the other side, because then we have a number on one side and a letter on the other; the statement is "if there's a number on one side, there's a blank on the other".
If the blank has a letter on the other side, that has no relationship to the if-then statement (it starts with "if there's a number on one side" and there's no number), so it won't make the statement false. Here's an analogy: suppose you have a bottle that says "If you drink this poison, you will get hurt." You decline to drink the poison. That doesn't make the if-then statement false! It just means the hypothesis (the first part) never triggered in the first place. The only way for an if-then statement to be false is if the first part is true and the second part is false.
Log in to reply
what i'm seeing is, "check if the following statement is true for the two cards" - emphasis on the two cards. "If a card has a number on one side, then it is blank on the other."
- card 'C' in alphabetical. thus it's exposing enough information to declare that this card fails the condition and can be left alone.
- card 'blank' meets one of the conditions. turning it over would satisfy the task, "check if the following statement is true for the two cards."
thus we would know if the statement is "true for the two cards." actually, after writing this it can be argued that we don't flip anything over because the statement can't be true for the two cards as the first card violates the conditional.
i believe this question highlights difference between whatever course backs this and computer code-think. /shrug
Log in to reply
@Camilo Santana – This problem is not derived from computer code logic. It is Material Conditional logic, for conditional statements - which occur when the statement is in the form 'if..., then...'.
A conditional statement can only be false when the antecedent (the if) is true, and the consequent (the then) is false.
With the second card (blank), the conditional statement will always be true (for that card). If there is a number, then the statement is true. If there is anything else, the statement remains true (due to Material Conditional logic) - hence we don't need to check it.
With the first card (C), we don't know yet whether it forces the conditional statement to be false (for that card, and thus for both cards), because we don't know if there is a number on one side - hence we need to check it.
One proves something is true by virtue of proving that it is not false.
and to go off your explanation, "if there's a number on one side" - perhaps the intent was "if there's a number on the top side" to make the intent clearer.
Log in to reply
@Camilo Santana – The intent is "on one side". The displayed face is not necessarily the antecedent for this conditional statement.
The question is either missing a condition or the given "correct" answer is in matter of fact incorrect!
The combinations are as follows if we turn the C card:
a) The hidden side of the C card is a number or blank, then the statement for the C card is false and thereby false for both cards (as the condition is that it must be true for both cards)
b) The hidden side of the C card is any other character or symbol, the statement is true for the C card (it did not break any condition), but undetermined for the BLANK card (it could have any symbol or being blank to falsify the statement)
If we turn the BLANK card:
a) The hidden side of the BLANK card is NOT a number, then the statement is false for the BLANK card and therefore false for both cards (again, as the condition is that it must be true for both cards)
b) The hidden side of the BLANK card is a number, then the statement is true for the BLANK card, but undetermined for the C card (it could have number or being blank to falsify the statement)
As a consequence of it, one must turn both cards to determine if the condition is true or false for both cards.
Log in to reply
If we turn the BLANK card:
a) The hidden side of the BLANK card is NOT a number, then the statement is false for the BLANK card and therefore false for both cards (again, as the condition is that it must be true for both cards)
Let me make a conditional statement: If it is raining, I will stay at home!
If it is not raining, and I go outside, have I broken my rule?
With what you've just commented, your answer should be yes. But actually the answer should be no - The statement remains true until it is broken.
This is how conditional statements operate.
Log in to reply
In which sense does your conditional statement apply to the given problem or to my statement. I don't see the equivalent. Here is how you make it equivalent...
Instead of Cards we use Houses and Windows we can look through:
House 1 ("C" Card): There is any weather, but no rain (C), and we don't know if anyone is at home (possible NUMBER on hidden side of card) House 2 (BLANK Card): There is rain (BLANK), but again we don't know if anyone is at home
You can look through the window to determine if anyone is at home. Through which window would you look to determine if following conditional statement is true FOR BOTH HOUSES...
If it is raining (side on is BLANK), I will stay at home! (other side is a NUMBER)
If you look into House 1 and no-one is at home, all you know is that with any weather (that is not rain), no-one is at home. That doesn't tell you anything about House 2 or the validity of the conditional statement.
If you look into House 1 and some-one is at home, all you know is that with any weather (that is not rain), some-one is at home. Again, that doesn't tell you anything about House 2 or the validity of the conditional statement.
If you look into House 2 and no-one is at home, you know the statement is true for House 2, but it doesn't tell you anything about House 1 or the validity of the conditional statement. Some-one could be in House 1 (not breaking any rules), but invalidating the statement.
If you look into House 2 and some-one is at home, you know the statement is false for House 2, and therefore you invalidated your statement.
Log in to reply
@Flex Domino – Let me further explain where the inaccuracy in the original problem is: Although not expressively put down as a rule, we have 3 possible values: C ("C"), N (any Number), B (Blank). As no rules have been pinned down about the possible combinations, the following combinations of card sides are possible (not applying the conditional statement)
C-C C-N C-B N-C N-N N-B B-C B-N B-B
You have the two combinations
C-? B-?
The possible combinations for the two given cards are the following:
C-C C-N C-B B-C B-N B-B
It is basically not possible to determine if the statement B-N or N-B is true for a given stack of 2 cards by looking up only one card.
Log in to reply
@Flex Domino – I recommend reading my reply to Reed Thomas's comment on this solution.
Log in to reply
@Jonathan Quarrie – I replied under this posting, but in short your answer is incorrect.
@Flex Domino – I have also provided my own solution, which further elaborates on how to solve this problem.
- B-N is true, because there is a number and the other side is blank.
- B-C is vacuously true , because there is no number (the "if" is not true).
- B-B is vacuously true , because there is no number (the "if" is not true).
but what if on the other side of the blank card there was another blank side
Log in to reply
That doesn't make the statement false. The statement is
If it has a number on one side, it has a blank on the other.
not
If it is blank on one side, it has a number on the other.
The second statement is very different. Compare:
If he plays basketball, he's an athelete.
with
If he's an athlete, he plays basketball.
Definitely not the same!
Hmmm, so Blank -> Number is not equals to Number -> Blank, for which reason the Blank card is irrelevant (always true, because it does not falsify the statement either way), but C -> Number is FALSE? Why? Because in converse (!) Number -> C would falsify the statement? I thought the converse is a different thing, so C -> Number is not Number -> C and therefore C -> Number is true as it does not falsify the statement. In matter of fact if the converse is a different thing, then C -> to anything would always be true, because it never falsifies the statement. In other words, I wouldn't need to turn any card to determine that the statement is true. Buah, the more I read the explanations, the more I get confused.
Log in to reply
Hi Flex, I don't aim to torment or further confuse you by replying to another one of your comments. I just want to try and add clarity.
The reason that C -> Number is false is because the conditional statement declares "If a card has a number
on one side
, then it is blank on the other.".
It does not say "If a card has a number
on the presented side
, then it is blank on the reverse."
- Presented side -> Reverse side
C -> N is false because
one side
has a number.
N -> C is also false because
one side
has a number.
Log in to reply
Jonathan, you are confirming my point!
Blank Morrison wrote "Consider the blank card: it does not matter whether or not there is a number on the other side because the statement is still true in either case." in addition the Challenge Master wrote "If a card has a number on one side, then it is blank on the other...with...If a card has is blank on one side, then it has a number on the other...These are very different! The second is called the converse of the first. "
Either one of you is correct. Either the converse is a different combination set or the converse is not. So either C->N EQUALS N->C or it is NOT EQUALS.
If I interpret your words correctly..."It does not say "If a card has a number on the presented side, then it is blank on the reverse."", then C->N EQUALS N->C. However, Blank Morrison and the Challenge Master are stating the opposite: C->N NOT EQUALS N->C.
Only one of you can be correct. In any case, I challenge both you explanations!
Log in to reply
@Flex Domino – To refine my criticism to Blank Morrison and the Challenger's explanation:
Taking the offered logic of B->? always being true because it does never break the rule N->B, as B->N is not the same as N->B, one must apply the same logic to C->?, it will never break the rule as C->N, C->B or C->C are not breaking the converse asymmetric rule of N->B. As a result and as stated before, I do not need to turn any card to know that the statement is always true for both cards.
If in the contrary you are correct and there is no converse asymmetry, then you need to turn both cards (as explained to you in my previous postings).
Log in to reply
@Flex Domino – A card with a C on the front, and N on the back is a card with N on the front and C on the back.
But a card with B on the front does not imply N is on the back.
This is the distinction.
Log in to reply
@Jonathan Quarrie – Jonathan, you have not addressed my comment. And you answer is inconsistent. The first sentence considers a determined set C->N and N->C, which are either equal or not, depending on symmetry. The second sentence is a non determined set of B->?, which of cause can be either B->B, B->C or B->N (and therefore N is indeed not implied. Again, this is not in any way a valid reply to my previous posting.
@Flex Domino – The fact that the antecedent and the consequent share the same medium complicates the situation.
There is no converse logic involved in my assertion about comparing the following situations:
- The presented side being C and the reverse side being N.
- The presented side being N and the reverse side being C.
C is the consequent in both situations, because N triggers the antecedent condition to be true.
Log in to reply
@Jonathan Quarrie – Well, whether there is a converse asymmetry involved or not must be part of the statement of this challenge, which it is not. So the question is, can an asymmetry be implied? I would react like you and say NO!
However, we both disagree here with the Challenge Master, who stated that there is an asymmetry. Well, that is how I interpret his note above.
Log in to reply
@Flex Domino – I am NOT disagreeing with the Challenge Master. There is absolutely no converse logic required to solve this problem.
Two different scenarios having the same condition is distinct from two different scenarios having the same implication .
From N → B, you continue to assert B → N.
Presented side -> Reverse side
- C -> N is false because one side has a number.
- N -> C is also false because one side has a number.
I have used -> in this comment to indicate the turning of a card, not an annotation for implies ( → ).
The act of turned a card is not the same as a declaration of implication. Converse logic only applies to a declaration of implication.
I suggest that you raise a report, so that we can stop littering this comments section with replies. I am happy to continue our discuss further, but not here (or in disparate threads).
Log in to reply
@Jonathan Quarrie – Jonathan, you constantly contradict yourself.
1) "I am NOT disagreeing with the Challenge Master. " 2) "There is absolutely no converse logic required to solve this problem."
However, 2) is in contradiction to what the Challenge Master stated above...
"If a card has a number on one side, then it is blank on the other.
with
If a card has is blank on one side, then it has a number on the other.
These are very different! The second is called the converse of the first. "
So if you are saying that an asymmetry in the converse logic is not required, then you are in disagreement with the Challenge Master.
Anyway, I give up, because I have exhausted my arguments to show that the challenge is flawed.
If I flip the card with the letter and it does not have a number it does not prove nor disprove the statement, because there is no statement that says at least one card has a number.
I thought that you had to flip both cards because wouldn't it have to count only if both of the cards show the statement. I would rate this problem a 5 because it was kind of confusing. I felt confused because I though that you had to flip both cards.
Whether the other side is a number when one side is blank? I can't understand it.
The question seems to be incomplete: 1) the card with the 'c' can also be blank, the question never mentioned that "a card should have a number" is necessary. 2) Similarly the blank card can also have a character on the other side. This was also not mentioned. Making the question vulnerable to trivial outcomes. 3) Now if the question really is complete, then considering the above points, both the cards must be flipped in order to make sure if the statement is true or false.
"Challenge Master" do let me know if I am wrong here.
Log in to reply
You don't need to flip the blank card because no matter what is in the back, it doesn't violate the rule. For those of you who still don't understand, look at this anology.
Let's say the two cards represent two people at a bar. The first person drinks wine while the second person drinks fruit juice. Also the law says no underage drinking. You don't need to check the second person's age because you can't break the law if you drink fruit juice, but you need to check the first person's age because he/she might be underage drinking.
The statement is "If a card has a number on one side, then it is blank on the other."
So if you turn the C card and it has a number on the other side then the statement is false but if it has anything else than a number on the other side then nothing is proven regarding the validity of the statement because the statement only says something about numbers and not anything else.
Now if you turn the blank card and it has a number on the other side then the statement could be correct but the other card could still have a number on the other side which will falsify the statement, and same as the card with the C on it, if it has anything else then a number on the other side then nothing is proven regarding the validity of the statement because, once again, the statement only says something about numbers and not anything else.
Conclusion: You have to turn both cards to validate the statement.
Log in to reply
Conditions are binary. They have either been met (the condition is true) or they have not been met (the condition is false). We don't need to stated every other possible way of not meeting the condition to establish whether a statement about one explicit condition is true. It is implicit that anything other than the stated condition makes the condition false.
For example; When a law prohibits people under a certain age from drinking alcohol, do you need to be told a rule for every possible age over the restricted range before you can establish whether the law has been broken?
The law (conditional statement) remains upheld (true) until it is broken (false).
Material conditional statements remain vacuously true until they are proven to be false statements.
Log in to reply
Well if they remain true until broken then you wouldn't even have to check any card, now that doesn't seem right to me so tell me if I'm wrong
Log in to reply
@A. Hanblon
–
If the C card is turned, and there is a number on the other side, it contradicts the rule stating that if a number is on one side, then it is blank on the other - Making the statement false for that card.
However, if there is not a number on the other side, then the rule is not contradicted - Making the statement true for that card.
Because card C could be either true or false, it dictates whether the statement for both cards is true or not - So we must check it.
Log in to reply
@Jonathan Quarrie – If the C card doesn't have a number on the other side you're empty handed without knowing the validity of the statement, checking the other card could make the statement true if it has a number on the other side and you've checked all cards there are so it wouldn't be possible to falsify the statement anymore. I think you should always take the chance to validate the statement because it's better to know indefinitely that the statement could be true or false then just knowing the statement could be true or false while there is still a card left that could prove to be true
Log in to reply
@A. Hanblon – We can know with a certainty that the blank card does not contradict the statement, even without checking it.
- When there is a number on the reverse side, the statement for the blank card is true.
- When there is not a number on the reverse side, the statement for the blank card is vacuously true.
Relating this problem back to the analogy of underage drinking:
- A number on one side = under age.
- Blank = not drinking.
When someone is not drinking alcohol (blank), we don't need to check their age - This law cannot be broken if a person doesn't drink.
When someone is drinking alcohol (C), we need to check their age, to prove that they are not breaking the law.
What this problem is asking of us is equivalent to proving that two people are both upholding the law.
Agnishom Chattopadhyay's solution should be credited for this specific analogy.
The real biggest problem here that I haven’t seen anyone address yet is that the question asks about numbers and blank sides and yet the cards show a letter and a blank side. Therefore flipping the C card would be pointless as it has a letter not a number and therefore doesn’t even apply to the question.
Log in to reply
If there is a number on the reverse side of the card with C, then it would prove the statement to be false, because there would be a number on one side, and the other side would not be blank - contradicting the statement.
There are two kinds of people in a party - those who are drinking and those who are not.
As the security officer, you must ensure the following:
If a person is under 18 years, then they should not be drinking.
Which people should you ask their ages?
Compare the above scenario with the problem.
C corresponds to drinking, Blank Corresponds to not drinking. Having a number corresponds to being below 18, not having a number corresponds to being at least 18.
This is the best explanation, thank you for helping me to understand.
Awesome analogy! Not only does this explain the situation, but it is a practical application of logic skills!
nice analogy!
Brilliant solution👏👏👏👏
You have 4 possibilities in your answer: drinking/under 18, not drinking/under 18, and 2 more for over 18. With the cards you have 6: C card other side blank (1), number (2), or something other than blank/number (3), blank card other side blank (4), number (5),or something other than blank/number (6). That is why I think that turning both cards is necessary.
Log in to reply
The second, blank card corresponds to someone who is not drinking.
You are worrying that people under 18 might be drinking. Do you need to check someone who is not drinking?
Log in to reply
No. And that is why the mentioned drinking analogy would be correct iff there were two possible card faces in original question (for e.g. blank and non-blank). But there are three: blank, number, and anything else (for e.g. a letter which is shown). Even if you consider C a number, the other side of both cards can show a random figure which is neither blank nor number so there are 3 possible card faces. The designated answer would be correct only if "something" instead of "number" had been written in the question.
Log in to reply
@A Former Brilliant Member – "If a card has a number on one side, then it is blank on the other." can be false in one and only one case:
The card has a number on one side
and
the card is not blank on the other side.
It is impossible for the second card to fulfill such conditions. If it has a number on the other side, the if-then works out. If it has a letter, flower, or other symbol on the other side, the if-then never triggers in the first place. It never needs to be checked.
@A Former Brilliant Member – The number of possibilities of how the faces could be/are represented is irrelevant. This solution is conveying the concept of how to determine the truth of a statement by using only the checks that are necessary.
A statement is true until it is proven that it is false - I.e. A rule is being upheld (is true) until it is being broken (is false).
The statement in this problem is an explicit rule governing just one type of card face (a number).
In order to confirm that the statement is true in this scenario, we have to prove that the cards are not breaking the rule for the governed face.
There are 2 approaches to proving that something governed by a rule is not illegal (breaking the rule):
1. Check that something governed by a rule doesn't produce an illegal state.
2. Check that an illegal state has not been produced by something governed by a rule.
In the absence of a being presented a scenario with a card that has a number face, the only approach we can take is to see if the non-blank card (C) has got a face governed by a rule on the other side (number).
The blank face is not governed by a rule, and it is not an illegal state, so we don't need to check it.
C is not a number.
Log in to reply
.... indeed? It states that in the problem?
If you're thinking "consequently, I don't need to flip the first card", the problem happens if the card with a C has a number on the other side. Then the card has a number on one side and a letter on the other, when it is supposed to have a blank. With this answer this corresponds to finding someone drinking at a party, checking their age, and finding they are under 18.
Log in to reply
The problem happens if the card with C has anything that is not a number on the other side. Even if you consider C a number, as in hexadecimal for e.g., there can be some random figure.
Log in to reply
@A Former Brilliant Member – Yep, you've got it! That's why you need to flip the C. (Also, the problem does explicitly say "the letter C" so we know it is a letter.)
There's an explicit differentiation between letters and numbers in the description! If we differentiate between those, we would have to flip the blank card.... That problem has not been posed well....
Log in to reply
It does not matter what is on the other side of the blank card. With this answer it is like a person at the party who is not drinking. You don’t need to check their age.
Where did you see this? I remember seeing out in the world before
I equated it to if one person looks like they shouldn't be allowed in a bar then check all I.Ds of the party (flip both)
Agnishom Explanation really helpful
A coomon misconception is that people should flip the blank card. The blank card can either have a number or not, and the statement is still true either way.
The card you should flip is the C card. If it has a number then it's false.
EDIT: Flipping the C card is to check that the statement is not false. That means getting a blank or a letter does not mean the statement is false nor is it true.
https://www.youtube.com/watch?v=AOAtz8xWM0w
Two questions.. First, if the C card doesn't have a number what does it tell you about the statement. I think you can't say that the statement is true..no? Second, if the blank card doesn't have a number it tells you nothing about the other card, which may have a number and thus falsifying the statement..no?
Log in to reply
- You can reinterpret the sentence as "if one side of the card is not blank, then there is no number on the other side" which is the scenario you mentioned.
- The only way for an "if-then" statement to be false is to have the first sentence to be true and the second sentence to be false. In both sentences (the one mentioned in the question and the one mentioned above) the first sentence is false which means the whole statement is true regardless of the validity of the second sentence.
Just because you flip the C card over and find no number doesnt mean that the numbered card will be blank on the other side. The only case in which flipping the lettered card proves wheather the statement is true or false is if there is a number on its opposite side. If anything else is on the back of thenlettered card you still have no proof what the opposite side of a numbered card will have.
I disagree. This never said that the C card will have a number or a blank on the back. What if it has a letter on the back? that will not answer the question!
Picking up both cards is allowed. And would yield the same information. It’s not the most effecient, but efficiency of validation of statement isn’t required. Not elegant, but not untrue. Not very “brilliant”
by flipping the blank card, it is undetermined, not "still true". I like this puzzle. got me good
But if it doesn’t then you still don’t know
Log in to reply
Well if something hasn't been proven wrong, then it's right.
By the way guys, this is my first solution to a problem. The argument in this section is very motivative. Thanks to all of you!
I think this is a very poor question.
Most compilers would throw an error that you have unreachable code in the case that there are no numbers printed on either card (if 0 == 1)... It's an irrelevant question, but to know that the question is unrelated to the cards does require turning both.
It's poorly worded questions like this that turn people off maths.
What if neither card has a number printed on either side? How do we know if the statement is true or not? I agree with Isaac Westwood, this is a very poorly worded question. The question states "you want to check if the following statement is true for the two cards" but if both have no numbers, we can't say for certain if it's true or not. It's irrelevant.
If the second card has a number on the other side, the statement can still be true.
If the second card does not have a number on the other side, the statement can still be true.
If the first card has a number on the other side, the statement cannot be true.
If the first card does not have a number on the other side, the statement can still be true.
The first card is the only card which might contradict the statement, so we need to flip that card only.
But you want to check if the statement IS true.
Log in to reply
Yes. However, the only possibility that might be false is the back of card C. To check validity, we need to ensure there is not a number on the other side of C.
Log in to reply
What happen if the first card is blank on the other side?.
Log in to reply
@Roberto Lazarte – The statement would still be true. The statement only applies if there is a number on the card. However, if there is a number on the other side of the first card, the statement would be false. We have to check the first card to ensure that there is no number on the other side of the card.
If the first card does not have a number on the other side, the statement can still be true. If the first card is blank on the other side, the statement can still be true. Then. If the second card has a number on the other side, the statement is true. We need both cards,
Log in to reply
That does not explain why we need to check both cards. Could you please go into detail about why we should check the second card?
Log in to reply
Because, thinking outside the box, is possible that the first card is blank on the other side; and in this case, we should check the second card (the statement can still be true). If the first card is blank in one side, and the second card have a number, the statement is true.
Log in to reply
@Roberto Lazarte – The goal is to look for situations where the statement is FALSE and showing that these situations do not exist. By showing that something cannot be false, it is true by default. The ONLY way for this situation to be false is if there is a number on the other side of the first card. By checking the first card only, we will automatically know if the statement is true or false, no matter what is on the second card.
I'm going to try and address a range of reasons for why some people have been getting this problem wrong, and then I will solve the problem.
- Confusion/misconceptions about checking that the statement IS true.
- Understanding conditional statement logic.
- Explicit vs Implicit
- Incorrectly using converse logic.
- Solving the problem
1. Confusion/misconceptions about checking that the statement IS true :
- Checking that something IS true, is the same as checking that it IS NOT false.
- In a different context, a substance is considered to be pure by the absence of impurities.
Only when you have eliminated the possibility of falsities existing can you determine that something is true.
2. Understanding conditional statement logic
A conditional (if, then) statement is asserted in this problem. Conditional statements have the following details:
- Adheres to Material Condiational logic.
- The 'if' part is called the Antecedent ( p ).
- The 'then' part is called the Consequent ( q ).
-
p
→
q
- → is the annotation for implies .
- The material conditional only states that q is true when (but not necessarily only when) p is true, and makes no claim that p causes q .
-
A conditional statement is
only
false when the condition of
p
is true, and
q
is false.
- When p is false, the statement is vacuously true .
Here's an example:
Conditional statement: " If it is raining, I will stay at home. "
| Case | ( p ) Raining | ( q ) Stay at home | Result |
| 1 | True | True | T r u e |
| 2 | True | False | F a l s e |
| 3 | False | True | T r u e |
| 4 | False | False | T r u e |
- If it is raining, and I stay at home; I have not broken my rule - The statement remains t r u e .
- If it is raining, and I go out; I will have broken my rule - The statement is now f a l s e .
- If it is not raining, and I stay at home; I have not broken my rule - The statement remains t r u e .
- If it is not raining, and I go out; I have not broken my rule - The statement remains t r u e .
How does this relate to the problem?
-
p
- In my example, p is true when it is raining , and false when it is not raining.
- In this problem, p is true when a card has a number on one side , and false when there is not a number on one side.
-
q
- In my example, q is true when I stay at home , and false when I do not stay at home.
- In this problem, q is true when the other side is blank , and false when the other side is not blank.
3. Explicit vs Implicit
In all cases,
anything
other than what is explicitly stated will render the
condition
as false.
It's implicit that we don't need to state rules for every possible thing before we can apply conditional logic to them.
For example:
- The letter C is not a number ( p = false), and it is not blank ( q = false).
- A tree is not a number ( p = false), and it is not blank ( q = false).
- Blank is not a number ( p = false).
4. Incorrectly using converse logic.
Converse logic
can be used when
p
and
q
are equivalent.
For
p
→
q
, when
p
and
q
are equivalent, it allows us to assert
q
→
p
.
Here's an example:
- "If I am a triangle, then I am a three-sided polygon"
- "If I am a three-sided polygon, then I am a triangle"
The definition of "triangle" is "three-sided polygon", thus the use of converse logic for the above statements is correct - Both are always true.
However, here's an example of when using converse logic is wrong:
- "If I am in Paris, then I am in France."
- "If I am in France, than I am in Paris."
A person can be in France without being in Paris, thus the use of converse logic for the above statements is wrong - The 2nd statement can be true, but it isn't necessarily true.
For this problem, the use of converse logic is wrong, because blank is not equivalent to a number - A blank face does not necessarily imply that the other face is a number.
By implying that the a blank face results in a number on one side, you are then forced to prove that assertion - leading you to having to check the blank card.
5. Solving the problem
With all of the above in mind, in order to check that the statement in this problem IS true, we must eliminate the possibility that falsities exist for the conditional statement within the given scenario.
Where in the scenario is there the possibility that the conditional statement could be false?
Neither of the card faces presented to us match the condition for the Antecedent ( p ) being true (they are not numbers), so we can consider each of them as a Consequent ( q ).
-
A blank face means that
q
is true.
- This corresponds to cases 1 and 3 from the table above.
- When q is true, the conditional statement for that card is always true.
By this application of conditional logic, we know that the possibility for falsities for the conditional statement does not exist with the blank card. We gain no further sense of truth about the statement, so we don't need to check it.
-
A non-blank face (C) means that
q
is false.
- This corresponds to cases 2 and 4 from the table above.
- When q is false, the conditional statement for that card could be either true or it could be false (depending on whether p is true or false).
If either card is false (breaks the rule), it renders the statement covering both cards as false.
As the only card that has the possibility of falsities for the conditional statement, it's only necessary to check Just the card with C to determine whether the statement is true (or not) for both cards.
Bonus
Let's consider the statement in this problem in relation to a different scenario with just 1 card:
- "If a card has a number on one side, then it is blank on the other."
Is the statement true when there is a number on both (two) sides of the card?
"By an application of logic, we know that the possibility for falsities does not exist with the blank card."
I fail to see this logic and it is a questionable argument too. The blank card can either have a number, a C or be blank on the other side. With which argument do you conclude that the 2 possible falsities can be excluded by logic looking at the first card?
Log in to reply
Material conditional statement logic states that the conditional statement is only ever false when the Antecedent is true and the Consequent is false.
The Antecedent condition is only ever True for this problem's statement when the face has a number on it.
The Blank face (whether considered an Antecedent with a condition of False, or a Consequent with a condition of True), always results in the conditional statement being true for that card.
The pair of cards need to both be true for the statement for both cards to be true. When the Blank card is inherently true (regardless of what is on the other side), we only need to check the card with C to confirm that statement is either true or false for the pair of cards.
Log in to reply
Jonathan, I'm not arguing that your explanation for material conditional logic is wrong, I argue that material conditional logic does not apply for the problem the way it was/is laid down. The causal relationship is not given. Please refer to my other posting where I explained in detail what combinations of cards are to be taken into account according to the laid out problem. You can't establish the causal link unless the problem is refined in its conditions.
The only way that I'm incorrect is if I have misread or misinterpreted the original problem and the combination of possible cards is not as I argued in my other posting. Maybe that is due to the fact that normal language is a difficult tool to describe mathematical problems.
Log in to reply
@Flex Domino – I know it's difficult, I'm trying to find a way to explain that you may understand.
I'll cover what I think are the biggest points of contention between our arguments.
- Converse Logic
- In which sense is my conditional statement ("If raining, then home") equivalent to the problem's statement?
- Independent assessment vs Generalisation assessment
1. Converse Logic
Returning back to your original argument:
If we turn the BLANK card: a) The hidden side of the BLANK card is NOT a number, then the statement is false for the BLANK card...
This is converse logic , which is attempting to make "If Number, then Blank" equivalent to "If Blank, then Number".
Compare:
- If I am in Paris, then I am in France
- If I am in France, then I am in Paris
Converse logic can only work when the Antecedent and the Consequent are equivalent.
Number != Blank
Thus, the Blank card in this problem does not represent the condition for the Antecedent being true - which is what you are asserting.
The 'If' in this problem can only be True when there is a number.
2. In which sense is my conditional statement ("If raining, then home") equivalent to the problem's statement?
- If it is raining, then I will stay at home.
- If a card has a number on one side, then it is blank on the other.
| Antecedent (If) | Consequent (Then) | |
| Problem | Number / Non-number | Blank / Non-blank |
| Me | Raining / Not Raining | Stay home / Go out |
- Raining = Number
-
Not Raining = Non-number
-
Blank = Stay at home
- Non-blank = Go out
The "If" in my statement can only true when it is raining.
3. Independent assessment vs Generalisation assessment
The conditional statement is applied to each card independently.
The truth of each independent card then contributes towards the generalisation of the statement for both cards.
Below is a table that shows the possibilities for each card's contribution towards the generalisation for this problem (after having its truth independently established in relation to the statement) - where at least one false renders the generalisation false.
| Case | C | Blank | Generalisation |
| 1. | True | True | True |
| 2. | False | True | False |
| 3. | True | False | False |
| 4. | False | False | False |
Case 3 and 4 are not possible because of conditional statement logic for the Blank card being a Consequent.
This is a good example of a problem requiring rational thinking, an aspect of intelligence not tested on IQ tests. Most people would say that the blank card should be flipped over, thinking that revealing a number would prove the statement true and a letter would prove it false. However, this is not correct, because revealing a number would not prove the statement true in all cases, and revealing a letter would not prove it false, since the statement didn't say that all blank cards must have a number behind them, only that all numbers must have a blank behind them. So, the only way to prove this statement false is to find a letter with a number, since it would mean that not ALL numbers have a blank behind them. This is why the "C" card must be turned over instead.
The only way for this statement to be false is for a card to have a number on one side and a C and a number on the other. By this logic, you should check the card with the C.
The blank card doesn't affect whether the statement is true or not. If it has a number on the other side, it is true. But if it doesn't have a number on the other side, it is still true.
Since neither card shows a number, one can instead use the logically equivalent contrapositive statement: "If it's not blank on one side, then there's not a number on the other side." So flipping over the card with the letter "C" will confirm whether or not the statement is true.
You need to check the statement and its contrapositive. Therefore, you need to flip any card that has a number and any card that is not blank.
请问你是那个毕啸天公众号"毕导"的欧拉王吗?
The most concise solution so far (I got the correct answer myself in a matter of seconds because I am familiar with such problems). I am frankly amazed that on this site a question as easy as this has generated so many wrong answers.
In everyday use if ... then ... can have two meanings, and we usually understand which by the context. One is the conditional statement: if my house catches fire (then) I will go outside, the second is biconditional, if and only if abbreviated to iff : if a building catches fire (then) I will call the fire brigade.
In the context of a logic question we can assume a conditional statement, which is evaluated as true or false based on the truth values of the simple statements according to the following truth table.
| P | Q | If P then Q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
That is, the statement is only false if P (a card has a number on one side) is true and Q (it is blank on the other) is false.
Whether the blank card has a number on the other side or not, the compound statement is true: TT and FT both evaluate to T.
If we check the C card and find it has a number on the other side we would have TF, which would prove the statement false.
The statement "If a card has a number on one side, then it is blank on the other" is different from "If a card is blank on one side, then it has a number on the other." Basically, we only have to check if there is a number on the card with a "C" to see if it has a number. After all, there is no rule saying that blank cards must have numbers, but there is one saying that a number card must be blank. This photo may help:
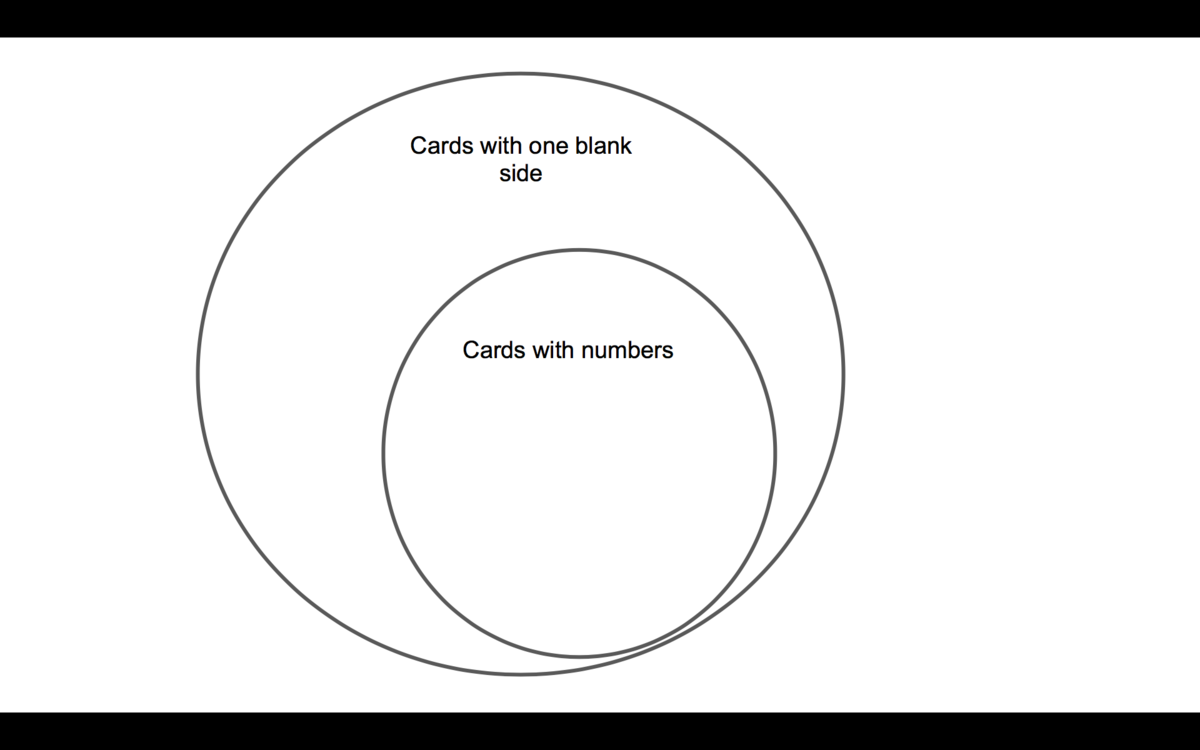 It shows that ALL number cards must be blank, and that SOME blank cards are number cards.
It shows that ALL number cards must be blank, and that SOME blank cards are number cards.
• If the card is blank on one side then it is bound to have a number on the opposite.
• We only have to flip the card containing the "C" because we already know what is on the other side of the blank one (As said "A number").
• By flipping the "C" card we can see what is contains on the other side, and then compare them.
Lots of people here bring up good points about the possibility of not being able to fully verify the statements truth. If the lettered card is flipped and doesn't have a number, then you would need to flip the blank card to fully verify. I think a better query to this question would have been "Which action would render the following statement false"? OR Supplement the initial information to claim that a number exists at all.
The statement "if A then B" (aka. "A implies B") can be true even if A never happens. For example it is true that if it snows in the Sahara then camels will get cold. You do not need to check the weather report to say this is true.
Easy,just ignore that except that statement,then pick the card with C
Consider the blank card: it does not matter whether or not there is a number on the other side because the statement is still true in either case.
Consider the C card: You need to check the C card because the statement will be false if there is a number on the back.
Therefore, the C card is the only card you need to flip.
Edit for clarity :
Examine the table below of all possible scenarios:
There is a number on the back of a non-blank card. Therefore, the statement is false. Verification is only needed on the C Card.
There is a number on the back of a non-blank card. Therefore, the statement is false. Verification is only needed on the C Card.
All cards that are not blank do not have numbers on the back. Therefore, the statement is true. Verification is only needed for the C Card.
All cards that are not blank do not have numbers on the back. Therefore, the statement is true. Verification is only needed for the C Card.
In all the scenarios, you only need to check the C Card. If you have any questions about this specific edit, tag me in your comment.