Calculating distances might not be easy
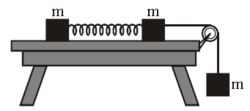 On a smooth horizontal table are two identical cubes of mass
m
, connected by a spring of spring constant
k
. The length of spring in the unstretched state is
L
. The right cube is linked to the load mass
m
at the end. At some time the system is released and the system moves without initial velocity. Find the maximum distance (in
cm
) between blocks during the motion of the system.
On a smooth horizontal table are two identical cubes of mass
m
, connected by a spring of spring constant
k
. The length of spring in the unstretched state is
L
. The right cube is linked to the load mass
m
at the end. At some time the system is released and the system moves without initial velocity. Find the maximum distance (in
cm
) between blocks during the motion of the system.
[ L = 1 cm , m = 3 kg , k = 1 0 0 0 N/m ].
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
@Kishore S Shenoy Can you justify your conservation of energy equation? It seems you are making the assumption that x will be maximized at a point when there is not kinetic energy in the system.
Log in to reply
That is in the block frame, at maximum point, relative velocity is zero. And work energy theorem is true for any frame thus conserving it in the accelerating frame of the block.
What is basis of your dynamic equations? I don't get your frame.
Let blocks 1, 2 and 3 be numbered from left to right. The equations of motion for each block are
m g − T = m a 3
T − k x = m a 2
k x = m a 1 ,
where x is the elongation of the string and blocks 2 and 3 have the same acceleration (say, a 2 ) because they are equally spaced by the string at all times. Let x 1 and x 2 be the positions of blocks 1 and 2 with respect to some reference frame. We then have
x 2 − x 1 − L = x or
a 2 − a 1 = d t 2 d 2 x .
Finding a 1 and a 2 from the equations of motion and replacing them on this last one, we get the differential equation for x
d t 2 d 2 x + 2 m 3 k x = 2 g ,
which solution is
x = − 3 k m g cos ( ω t ) + 3 k m g .
Given this, the maximum value of x is when cos ( ω t ) = − 1 , i.e. 3 k 2 m g . Hence, the maximum distance between blocks 1 and 2 should be
L + 3 k 2 m g = 3 cm,
given g = 1 0 m / s 2 .
You do not have to do all this.
Log in to reply
There are always several solutions to one problem which lead to a common answer. This is mine, I would like to read yours! =)
Log in to reply
Take the two blocks on the table to be one system. Thus
a = 3 g
LOL. It's like using Lagrange for an Atwood Machine Problem
Log in to reply
What? What are talking about?
Log in to reply
@Kishore S. Shenoy – Lagrangian mechanics is an approach to solving complex problems by using energy rather than dealing with forces. It is very, very useful in engineering but in some simple problems with only a couple of forces it is not effective. Plus the calculus behind Lagrange is pretty simple. To define Lagrange function (L) we use energy and differentiate. it is just a very useful tool that i use for hard problems though it requires solving partial differential equations. \frac{d}{dt}\left(\frac{\partial \:}{\partial x\left(dot\right)\:}\left(L\right)\right)=\frac{\partial }{\partial x}\left(L\right)
First analyze block falling down.
mg - T= ma
Now understand that we can associate the spring block system as that of a block of mass 2m.
So we analyze than T=2ma
mg-2ma=ma ; ma+2ma = mg ; 3ma= mg a = g/3
NOW PLUG BACK IN T=2ma ; T=2mg/3
Now anaylaze system in depth.
T-kx=0 ; T=kx ; 100 * 2mg/3k = x (* 100; to convert to centimeters) x+1 = 3
TADA!
The acceleration of centre of mass will be g/3.(Mg=3Ma) Now,let us view everything from the centre of mass frame.When the spring is at it's maximum extension the velocity of all three blocks with respect to centre of mass will be 0.(This statement can be proved using Proof by Contradiction) Now writing kinematic equation of velocity for the leftmost block. V^{2}=integral of 2 a dx. The value of a is the acceleration of the leftmost block with respect to centre of mass frame. Hence a= (g/3)-(kx/m) Now,if we make the integral 0 we get value of x as 2cm.This is maximum extension in spring.Adding the initial distance between the blocks to it.We get maximum distance between them as 3cm.
Taking forces on the whole system,
m g a = 3 m a = 3 g
W.R.T to the block at the leftmost end, forces acting on the other block on the table are k x , k x and 3 2 m g .
Thus conserving energy in the block frame,
0 x = − k x 2 + 3 2 m g x = 3 k 2 m g
∴ x = 3 k 2 m g