Calculator Not Needed!

Algebra Level 4

{ A = 1 × 2 + 3 × 4 + 5 × 6 + … + 37 × 38 + 39 B = 1 + 2 × 3 + 4 × 5 + … + 36 × 37 + 38 × 39 \begin{cases} {A = 1\times 2 + 3\times4 + 5\times 6 + \ldots+37\times38 + 39 } \\ { B = 1 + 2\times 3 + 4 \times 5 + \ldots + 36 \times 37 + 38 \times 39 } \end{cases}

The values of A A and B B are obtained by writing multiplcation and addition operators in an alternating pattern between successive integers as described above. Find ∣ A − B ∣ |A-B| .

Notation: ∣ ⋅ ∣ | \cdot | denotes the absolute value function .


The answer is 722.

View wiki
Ravi Dwivedi by Ravi Dwivedi , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Ravi Dwivedi
Jul 3, 2015

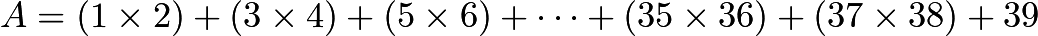
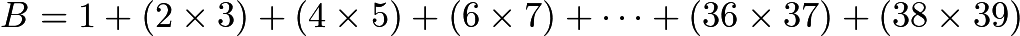Therefore

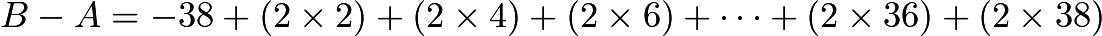
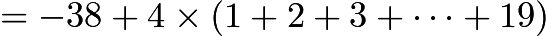
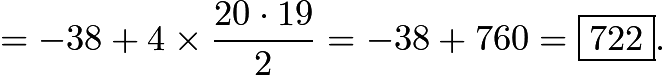
6 Helpful 0 Interesting 0 Brilliant 0 Confused

This appears much simpler if you write it in summation notation. We have,

A − 39 = ∑ k = 1 19 ( 2 k ) ( 2 k − 1 ) and B − 1 = ∑ k = 1 19 ( 2 k ) ( 2 k + 1 ) A-39=\sum_{k=1}^{19}(2k)(2k-1)\quad\textrm{and}\quad B-1=\sum_{k=1}^{19}(2k)(2k+1)

Subtract the first equation from the second to get,

( B − A ) + 38 = ∑ k = 1 19 ( 2 k ) ( 2 k + 1 − 2 k + 1 ) ( B − A ) + 38 = 4 ∑ k = 1 19 k = 4 × 19 × 20 2 = 760 B − A = 760 − 38 = 722 (B-A)+38=\sum_{k=1}^{19}(2k)(2k+1-2k+1)\\ (B-A)+38=4\sum_{k=1}^{19}k=4\times\frac{19\times 20}{2}=760\\ B-A=760-38=722

Hence, for this problem, we have,

∣ A − B ∣ = B − A = 722 |A-B|=B-A=\boxed{722}

In this problem, in the second line of calculation, we used the sum of first k k positive integers formula which is ∑ k = 1 n k = n ( n + 1 ) 2 \sum\limits_{k=1}^n k=\frac{n(n+1)}2 .

Prasun Biswas - 5 years, 11 months ago

Log in to reply

Thanks for an alternative!!

Ravi Dwivedi - 5 years, 11 months ago

Log in to reply

It's not an alternative solution. It's the same solution as yours but presented in a formal way using summation notation.

Prasun Biswas - 5 years, 11 months ago

Log in to reply

@Prasun Biswas – Yeah...same thing.....!!

Ravi Dwivedi - 5 years, 11 months ago

Exactly same solution

Kushagra Sahni - 5 years, 11 months ago
Chew-Seong Cheong
Oct 25, 2019

A = 0 + 1 × 2 + 3 × 4 + 5 × 6 + ⋯ × 36 + 37 × 38 + 39 B = 1 + 2 × 3 + 4 × 5 + 6 × 7 + ⋯ + 37 + 38 × 39 ⟹ B − A = 1 + 2 × 2 + 2 × 4 + 2 × 6 + ⋯ + 2 × 38 − 39 = 1 + 4 ( 1 + 2 + 3 + ⋯ + 19 ) − 39 = 1 + 4 × 19 × 20 2 − 39 = 722 \begin{aligned} A & = 0 + 1 \times \blue 2 + 3 \times \blue 4 + 5 \times \blue 6 + \cdots \times \blue{36} + 37 \times \blue {38} + 39 \\ B & = 1 + \blue 2 \times 3 + \blue 4 \times 5 + \blue 6 \times 7 + \cdots + 37 + \blue{38} \times 39 \\ \implies B-A & = 1 + 2 \times \blue 2 + 2 \times \blue 4 + 2 \times \blue 6 + \cdots + 2 \times \blue {38} - 39 \\ & = 1 + 4(1+2+3+ \cdots + 19) - 39 \\ & = 1 + 4 \times \frac {19\times 20}2 - 39 \\ & = \boxed{722} \end{aligned}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...