Calculus 2 - by Vlad Vasilescu (W)
n → ∞ lim n 1 + n 2 + n 2 2 + n 2 3 + ⋯ + n 2 n
Find the limit to 2 decimal places.
The answer is 1.44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Can you clarify what you mean by "AP formula"? I believe that you're using something differnt from arithmetic progression sum . I think what you want it:
( 1 − x ) ( 1 + x + x 2 + … + x n ) = ( 1 − x n + 1 ) .
Log in to reply
I meant GP sum formula, my bad
Log in to reply
Ah ic. I've edited that into the solution.
In future, you can edit your solution directly by hitting the "edit" button at the bottom of the solution.
Log in to reply
@Calvin Lin – I was trying to, and I did it before with other solutions of other problems, but my browser did not let me save the editions
Log in to reply
@Guilherme Niedu – Hm, can you elaborate on "browser did not let me save the editions"? What happened then?
@Calvin Lin – Thanks anyway!
Relevant wiki: Riemann Sums
L = n → ∞ lim n 1 + n 2 + n 2 2 + n 2 3 + . . . + n 2 n = n → ∞ lim n 1 k = 0 ∑ n 2 n k = ∫ a b 2 x d x = ∫ 0 1 2 x d x = ln 2 2 x ∣ ∣ ∣ ∣ 0 1 = ln 2 2 − 1 = ln 2 1 ≈ 1 . 4 4 By Riemann sums a = n → ∞ lim n 0 = 0 , b = n → ∞ lim n n = 1
The limit of summation should be from k=1 to k=n or k=0 to k-n-1.
I think first of all 1/n should be separated which will become zero.then rest of the things will be same as above
Log in to reply
L = n → ∞ lim n 1 + n 2 + n 2 2 + n 2 3 + . . . + n 2 n = n → ∞ lim n 2 n 0 + 2 n 1 + 2 n 2 + 2 n 3 + . . . + 2 n n = n → ∞ lim n 1 k = 0 ∑ n 2 n k
Log in to reply
But the limit of summation should be k=1 to k=n
Log in to reply
@Kushal Bose – What do you mean the limit of summation? I am quite sure my solution is correct. Refer to Riemann sums.
Log in to reply
@Chew-Seong Cheong – Your solution is correct but I am saying about lower limit and upper limit of summation that is it should be k=1 to k=n
Log in to reply
@Kushal Bose – No, I have shown that 1 = 2 n 0 , therefore the limit s are k = 0 to k = n .
Log in to reply
@Chew-Seong Cheong – But riemann sum is valid for k=1 to k=n or k=0 to k=n-1
Log in to reply
@Kushal Bose – No, I have shown that ∫ a b 2 x d x . a = lim n → ∞ n 0 and b = lim n → ∞ n n . The limits of integration follow those of summation. Refer to the wiki I have attached. I learned from it.
Even if k = 1 to k = n − 1 , still a = 0 and b = 1 because n → ∞ .
You are everywhere 😂
You come up with different but very good solutions , so I guess it's good .👍
And one more thing your handwriting is really beautiful!
Did the same! . the infamous Riemann's sum technique
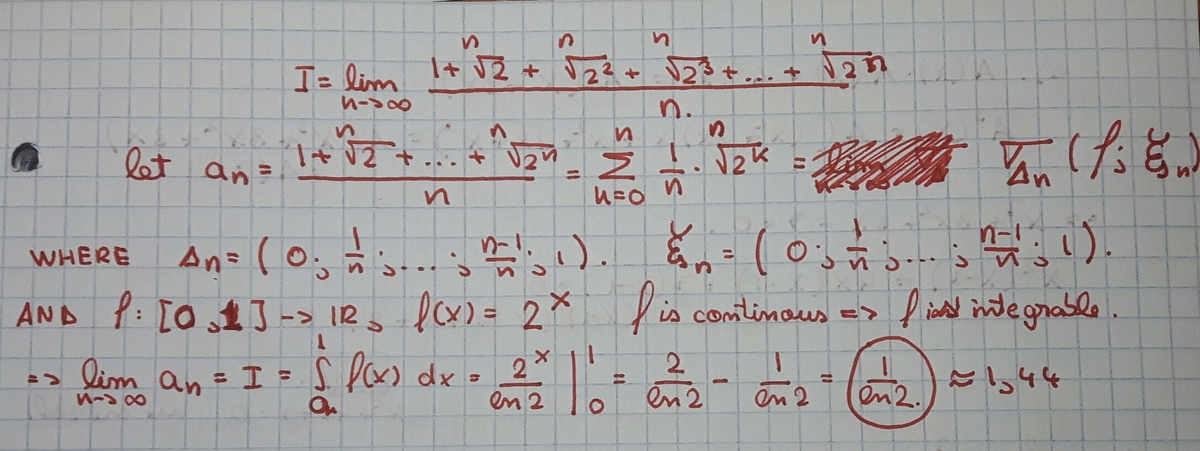
L = n → ∞ lim n 1 + n 2 + n 2 2 + n 2 3 + ⋯ + n 2 n
By the geometric progression sum formula,
L = n → ∞ lim n ( 2 1 / n − 1 ) 2 1 + 1 / n − 1
Set m = 1 / n , we get
L = m → 0 lim 2 m − 1 m ( 2 1 + m − 1 ) = ( m → 0 lim 2 1 + m − 1 ) ⋅ ( m → 0 lim 2 m − 1 m ) = m → 0 lim 2 m − 1 m
Applying L'Hôpital, we get
L = m → 0 lim 2 m ⋅ l n ( 2 ) 1 = l n ( 2 ) 1 = 1 . 4 4 . . .