Calculus For All
∫ ( x + x x + x ) x ( x + 1 ) x − 1 d x = 4 tan − 1 ( g ( x ) ) + C
If the above equation holds true for real-valued function g ( x ) and an arbitrary constant of integration C , find the value of ⌊ g 2 ( 1 ) ⌋ .
Notation: ⌊ ⋅ ⌋ denotes the floor function .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Chew-Seong Cheong , Thanks sir.
Can you please give me a solution to this problem also?
https://brilliant.org/problems/not-defined-really/?ref_id=1384444
"NOT DEFINED REALLY"
You have solved that.
I need that .
Log in to reply
I did. The one answer is 9 1 . Now it is ranked third.
Log in to reply
No, that was not your problem. You link above is not right.
Log in to reply
@Chew-Seong Cheong – SIr, i actually don't have hint to that problem.
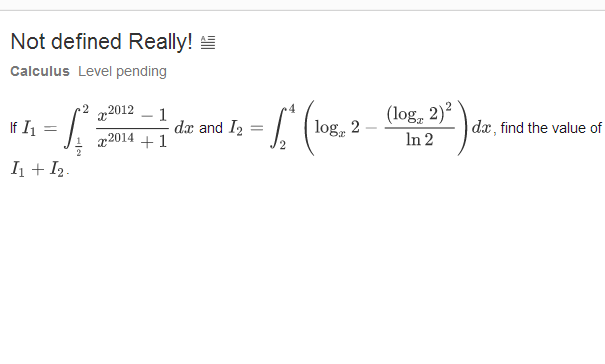
How you got I 1 ?
I have no solution for I 1 . I used Wolfram Alpha. Can you give a hint?
Nice solution. Can you please suggest me a good Calculus book?
Log in to reply
You can solve questions of brilliant they are really composed of good ideas and creative solutions besides this you can solve singage which I personally like it

Presenting @Ayush Sharma 's solution in LaTex.
I = ∫ ( x + x x + x ) x ( x + 1 ) x − 1 d x = ∫ x x + x x + x x x ( x + 1 ) x 1 − x x 1 d x = ∫ ( 1 + x + x 1 ) x + x 1 x 1 − x x 1 d x = ∫ ( 1 + u 2 ) u 4 u d u = ∫ 1 + u 2 1 d u = 4 tan − 1 u + C Divide up and down by x x Let u 2 = x + x 1 ⟹ 2 u d u = ( 2 x 1 − 2 x x 1 ) d x where C is the constant of integration.
Therefore,
g ( x ) = u = x + x 1 ⟹ g 2 ( 1 ) = 1 + 1 1 ⟹ ⌊ g 2 ( 1 ) ⌋ = 2