Wolfram Alpha Can't Do This, Can You?
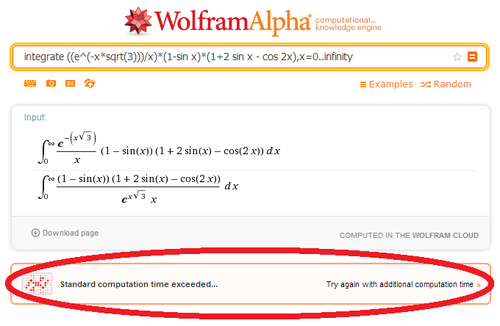 Today, when I was in my college library, I saw two engineer students were desperate to do their calculus homework. They became more frustrated when realized even
Wolfram Alpha
failed to answer it. I took a look their homework in case I could solve it. This is their homework:
Today, when I was in my college library, I saw two engineer students were desperate to do their calculus homework. They became more frustrated when realized even
Wolfram Alpha
failed to answer it. I took a look their homework in case I could solve it. This is their homework:
∫ 0 ∞ x e − x 3 ( 1 − sin x ) ( 1 + 2 sin x − cos 2 x ) d x = . . .
Could you help them out?
The answer is 0.7854.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Ah, I was so close. I missed a factor of 1 / 2 . :'(
Nice problem Tunk! :)
For those interested in the double integration method (and have no idea about Laplace transforms like me :P ) Tunk is talking about, see the following:
I evaluate ∫ 0 ∞ e − x 3 x sin x d x .
The above can be written as follows:
∫ 0 ∞ ∫ 0 ∞ e − x 3 sin x e − x y d y d x = ∫ 0 ∞ ( ∫ 0 ∞ e − x ( 3 + y ) sin x d x ) d y
= ∫ 0 ∞ ℑ ( ∫ 0 ∞ e − x ( 3 + y ) e i x d x ) d y
= ∫ 0 ∞ ( 3 + y ) 2 + 1 1 d y = ( arctan ( y + 3 ) ∣ ∣ ∣ 0 ∞
= 2 π − 3 π = 6 π
Similarly, the other integral can be also evaluated.
Log in to reply
You don't need to do double integration. Define I ( a ) = ∫ 0 ∞ exp ( − a x ) x sin ( x ) d x , for a ≥ 0 .
Now differentiate both sides with respect to a , where we use Leibiniz integral rule for the right hand side, to obtain
d a d I ( a ) = − ∫ 0 ∞ exp ( − a x ) sin ( x ) d x = − a 2 + 1 1
Hence, I ( a ) = − tan − 1 ( a ) + C . At a = + ∞ , the integrand is zero, Hence, C = 2 π . Thus the required integral = I ( 3 ) = 6 π
Log in to reply
Wow! That's cool. It never crossed in my mind using this one although one of my problem, Bizarre Integral , using this method. Thanks for pointing that out Abhishek. :)
That's much simpler than the double integrals. Thanks a lot for sharing this. :)
@Abhishek Sinha Can you explain how the "differentiating" part here worked in your post? im having trouble understanding that.
Poor you Pranav. It looks like today is your unlucky day (Trying to not remember that I was the only one who messed up your day. :D ). I hope tomorrow will be better than today. :)
Ohh, you tried to solve it by using double integral like I did when solving your problem? That's nice one! Although, I've to admit it that your problem is more difficult than this if you use double integral technique. I just want to try a 'new' method other than usual. You should learn Laplace and Fourier transform Integral! Those are powerful method Pranav. Are you engineering student? If so, eventually you'll study those topics.
BTW, I've posted the solution of Rolling Ball problem in case you want to see it.
Hi Pranav, could you please explain how you get the double integral? Also, could you refer me to some links that show the basics in solving problems using this method?
Log in to reply
Hi Anish!
I used the following:
x 1 = ∫ 0 ∞ e − x y d y
I hope you can take it from here. I haven't got any links which discuss this kind of method. Maybe Tunk can help, he seems to be more experienced in this stuff than me. :)
Also, this double integral method is used in the problem I shared: Definite Integral , how did you solve it if you did not use double integrals?
Log in to reply
@Pranav Arora – Well, I knew the integral : ∫ o ∞ e − ( x 2 + 4 ) y d y = x 2 + 4 1 beforehand.
But, that was a coincidence. I didn't know the general method of using double integrals for finding a certain type of integrals, even though I knew about double integrals (from Khanacademy)
Log in to reply
@Anish Puthuraya – I couldn't explain why crossed in my mind to use double integral method, it just like my intuition drives me to solve like that.
You may be interested to know & learn how members on Math Stack Exchange solve integral problems. I learn many integral techniques from that site.
I using gamma equation like this one
https://z-1-scontent-sin1-1.xx.fbcdn.net/hphotos-xpt1/v/t1.0-9/734970 1323318464361910 8843150876171050389 n.jpg? nc eui=ARgjJf8rbaQxS-dIjCdT VJsQvtRVcQ0_5XL6PKPdruzBRK525jRaISVeKGg&oh=797b5c4d98b84eeeafacd864f320ebb4&oe=57847A02
I did it using 'Differentiation of an Integral':
Assume I ( k ) = ∫ 0 ∞ x e − k x sin ( C x ) d x
Now differentiate w.r.t. k:
d k d I ( k ) = ∫ 0 ∞ x e − k x ( − x ) sin ( C x ) d x
Now, since x cancels from the numerator and denominator the resultant integral can be evaluated (using various methods such as Integration by Parts, Complex Numbers etc).
On integrating to obtain I ( k ) , a constant of integration has to be evaluated. For this find I ( ∞ ) : )
Log in to reply
Good job pal but a little bit advice, never plug in ∞ to replace the variable because infinity is not a number but merely a concept. You just write like this:
α → ∞ lim I ( α ) .
Log in to reply
Thanks a lot, I shall be more careful next time : )
You can evaluate the final integrals elegantly without using the Laplace transform methods by exploiting the rule of differentiation under the integral sign. See the solution that I posted in comment.
Well done, Tunk.
Hmmm... One of the parts of the equation is (1+2sinx-cos2x). But as cos2x-2sinx =1 transforms to 2sinx-cos2x=-1, the above part must be Zero and therefore the whole equation does not look good either??? Where is the error...?
Log in to reply
Did you dispute my problem by saying: "Since, 2 sin A cos B = sin ( A + B ) − sin ( A − B ) "? Well, sin ( A + B ) − sin ( A − B ) = 2 cos A sin B . Of course you may use this relation. If you use that, then in the final result we obtain A = x and B = 2 x , yield cos A sin B cos x sin 2 x sin 2 x cos x = 2 1 ( sin ( A + B ) − sin ( A − B ) ) = 2 1 ( sin ( x + 2 x ) − sin ( x − 2 x ) ) = 2 1 ( sin 3 x − sin ( − x ) ) = 2 1 ( sin 3 x + sin x ) . Thus, the result is still the same.
Who said cos 2 x − 2 sin x = 1 ??
definitly correct as the result, what a great problem
Beside, i'm 17 years old, i am vietnamese nice to meet you all
Ok. I have no idea what all you guys are talking about here, but I still solved the problem on the first try GUESSING the exact result of the integral. Good job, me.
Thumbs up! Abhisekh sinha!!!!!!(sorry if i have typed ur spelling of name wrong)
done it same way
Oopse...so close...!!but still couldn't reach the final ans..actually I'm a beginner at laplace transform...
by using wolfram we can solve very easily
NIntegrate[(Exp[-x Sqrt[3]]/x) (1 - Sin[x]) (1 + 2 Sin[x] -
Cos[2 x]), {x, 0, Infinity}]=0.785398
Log in to reply
As your suggestion, I input your code to W|A, but the result is unchanged. See this:
 Code by a Moron
Perhaps, you use Wolfram Alpha Pro.
Code by a Moron
Perhaps, you use Wolfram Alpha Pro.
Log in to reply
WolframAlpha will be happy to do this numerically. Substitute 0 in the prompt with 0.0 and it quickly returns the numerical approximation.
 WolframAlpha Prompt
WolframAlpha Prompt
what are you saying please tell me are you correcting my code or not??and please if it is any mistake then clear it.....
i started following you but can you teach me laplace transform ?
Mathematica /can/ do this integral exactly, it just needs quite a bit of time to do so.
WolframAlpha will be happy to do this numerically. Substitute 0 in the prompt with 0.0 and it quickly returns the numerical approximation.
 WolframAlpha Prompt
WolframAlpha Prompt
Yes, i did it , just like tunk :)
Manipulate the integrand as exp(-x√3)cos(x){sin(2x)/x} and integrate from {0 to infinity} in wolfram alpha to get answer=(π/4)=~0.785
Despite the fact that I've dealed with this integral before yet it took more than an hour for me to solve it. I believe you're better than me. This is my approach:
First, we manipulate the trigonometric function. ∫ 0 ∞ x e − x 3 ( 1 − sin x ) ( 1 + 2 sin x − cos 2 x ) d x = ∫ 0 ∞ x e − x 3 ( 1 − sin x ) ⋅ 2 ( sin x + 2 1 − cos 2 x ) d x = 2 ∫ 0 ∞ x e − x 3 ( 1 − sin x ) ( sin x + sin 2 x ) d x = 2 ∫ 0 ∞ x e − x 3 ( 1 − sin x ) ⋅ sin x ( 1 + sin x ) d x = 2 ∫ 0 ∞ x e − x 3 sin x ( 1 − sin 2 x ) d x = 2 ∫ 0 ∞ x e − x 3 sin x cos 2 x d x = ∫ 0 ∞ x e − x 3 ( 2 sin x cos x ) cos x d x = ∫ 0 ∞ x e − x 3 sin 2 x cos x d x = ∫ 0 ∞ x e − x 3 ⋅ 2 1 ( sin ( 2 x + x ) + sin ( 2 x − x ) ) d x = 2 1 ∫ 0 ∞ x e − x 3 ( sin 3 x + sin x ) d x = 2 1 ( ∫ 0 ∞ x e − x 3 sin 3 x d x + ∫ 0 ∞ x e − x 3 sin x d x ) From this point, it should be easier. You can either use double integral method like my solution in problem Definite Integral shared by Pranav Arora or you can use Integral Laplace transform . I prefer the second one because it's faster and simpler.
The Laplace transform of a function f ( x ) with x ≥ 0 is given by L [ f ( x ) ] = F ( p ) = ∫ 0 ∞ e − p x f ( x ) d x . Based on the table of Laplace transforms for f ( x ) = x sin a x , its Laplace transform is L [ x sin a x ] = tan − 1 ( p a ) . Therefore 2 1 ( ∫ 0 ∞ e − x 3 ( x sin 3 x ) d x + ∫ 0 ∞ e − x 3 ( x sin x ) d x ) = 2 1 ( tan − 1 ( 3 3 ) + tan − 1 ( 3 1 ) ) = 2 1 ( 3 π + 6 π ) = 4 π ≈ 0 . 7 8 5 4
# Q . E . D . #