Can f ∘ f be the opposite function?
As we can see in involving involutions , there are a number of functions f : R → R that satisfy the relation
f ( f ( x ) ) = x ∀ x ∈ R .
Is there any function f : R → R with the property f ( f ( x ) ) = − x ∀ x ∈ R ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
There is a slight typo here. In your definition of the first option, you mean f ( − x ) = − y , not y .
Great work - simpler than the solution I had in mind! I can see now that every possible function satisfying the requirement is of this form.
Here is an example of a family of functions
f
a
:
R
→
R
that have the property
f
a
(
f
a
(
x
)
)
=
−
x
,
∀
x
∈
R
.
(
a
can be any positive real number):
f a ( x ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ a x 0 − a 1 x x ∈ ( − a 2 k + 1 , − a 2 k ] ∪ [ a 2 k , a 2 k + 1 ) x = 0 x ∈ ( − a 2 k , − a 2 k − 1 ] ∪ [ a 2 k − 1 , a 2 k ) , k ∈ Z
Below, we can see what
f
2
(
x
)
looks like:
a nice simple fractal
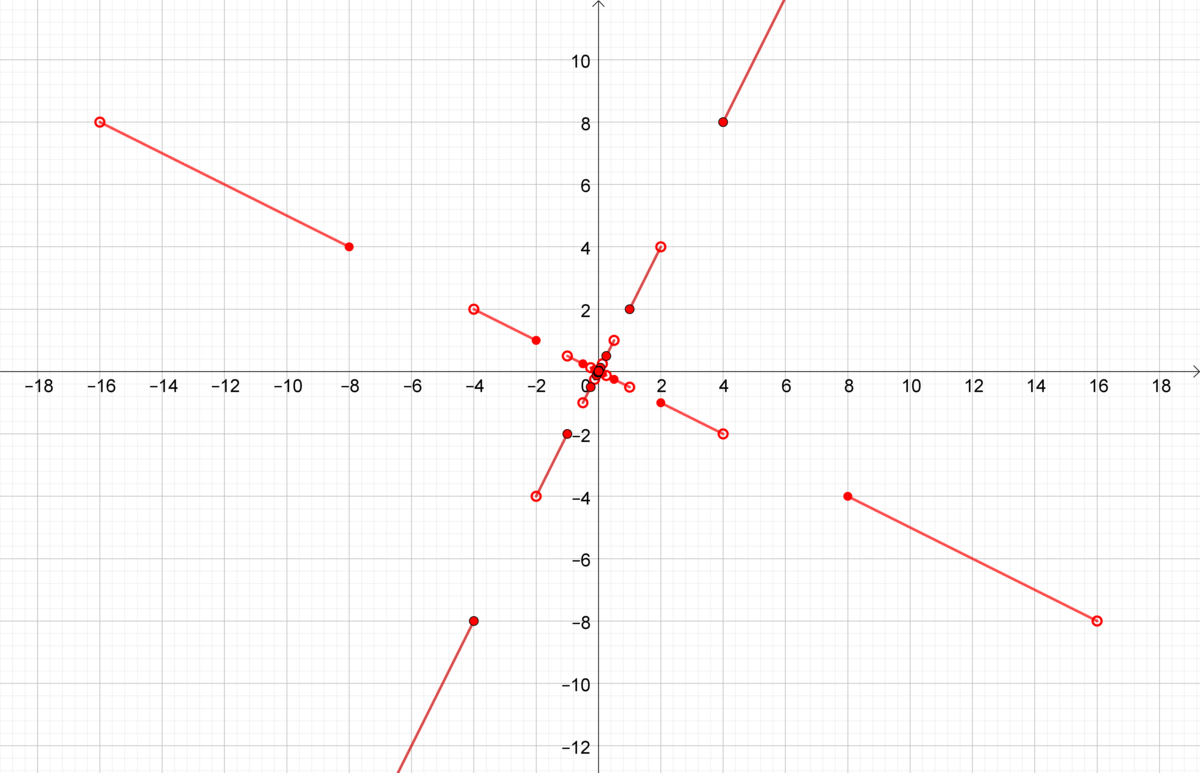
Nice drawing indeed. It puts some reality in the abstraction of the upper entries.
Merci bon toutou
Consider the subset V of C consisting of the strictly positive reals, together with the open upper half-plane. Thus V is the set of all complex numbers of the form r e i θ , where r > 0 and 0 ≤ θ < π .
Then V has the same cardinality as ( 0 , ∞ ) × [ 0 , π ) , which has the same cardinality as ( 0 , ∞ ) × ( 0 , π ) , which has the same cardinality as ( 0 , 1 ) × ( 0 , 1 ) , which has the same cardinality as ( 0 , 1 ) which in turn has the same cardinality as ( 0 , ∞ ) . Thus it is possible to find a bijection f : ( 0 , ∞ ) → V , in which case T f ( x ) = ⎩ ⎨ ⎧ f ( x ) 0 − f ( − x ) x > 0 x = 0 x < 0 is a bijection T f : R → C such that T f ( − x ) = − T f ( x ) for all real x If then follows that S f ( x ) = T f − 1 ( i T f ( x ) ) x ∈ R is a function S f : R → R such that S f ( S f ( x ) ) = − x for all real x . Thus we have a function of the right type (an "anti-involution"?) for each choice of bijection f : ( 0 , ∞ ) → V .
Since f ∘ h is a bijection from ( 0 , ∞ ) to V for each bijection h : ( 0 , ∞ ) → ( 0 , ∞ ) , and since there are infinitely many such bijections h , there are infinitely many "anti-involutions".
Could you give an example of such a function?
Log in to reply
Well, you could have a shot at implementing the various bijections which set up the chain of cardinalities I use.
1) A bijection f : [ 0 , π ) → ( 0 , π ) . Find any strictly increasing sequence x n with x 0 = 0 and 0 < x n < π for all n ≥ 1 . Then define f ( x ) = { x n + 1 x x = x n x ∈ { x n : n ≥ 0 }
2) A bijection f : ( 0 , ∞ ) → ( 0 , 1 ) . How about f ( x ) = tanh x .
3) It is easy to find an injection ( 0 , 1 ) × ( 0 , 1 ) → ( 0 , 1 ) (for example. you can interleave decimal expansions, so that f ( 0 . x 1 x 2 x 3 . . . , 0 . y 1 y 2 y 3 . . . ) = 0 . x 1 y 1 x 2 y 2 x 3 y 3 . . . where you can make this well-defined and injective by insisting on decimal expansions free of recurring 9 s, but finding a bijection ? The above function is not bijective (its range does not contain 0 . 1 9 0 9 0 9 0 9 0 9 0 9 0 9 . . . ). The Cantor-Bernstein Theorem tells us that a bijection exists, but does not really help us write one down.
Log in to reply
A bijection from the unit square to a unit interval can be via continued fractions. There exists a bijection from the reals to the irrationals, and each irrational has a unique simple continued fraction representation. Suppose x , y has the continued fraction representation x = [ 0 : x 1 , x 2 , x 3 . . . ] , y = [ 0 : y 1 , y 2 , y 3 . . . ] . Then ( x , y ) can be mapped to f ( x , y ) = [ 0 : x 1 , y 1 , x 2 , y 2 , x 3 , y 3 . . . ] , which is unique to ( x , y ) .
Log in to reply
@Julian Poon – OK, and we can write down an "explicit" bijection from the reals to the irrationals as follows: let ( q n ) n ≥ 1 be an enumeration of the rationals. Then define f by the formula f ( q n ) f ( q n + 2 ) f ( x ) = q 2 n − 1 + 2 = q 2 n + 2 = x n ∈ N n ∈ N x , x − 2 ∈ Q
For any real number n , the piecewise function f ( n ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ − x − n x − n 0 x + n − x + n if − 2 n k ≤ x < − 2 n k + n for any positive integer k if − 2 n k + n ≤ x < − 2 n k + 2 n for any positive integer k if x = 0 if 2 n k − 2 n < x ≤ 2 n k − n for any positive integer k if 2 n k − n < x ≤ 2 n k for any positive integer k has the property f ( f ( x ) ) = − x for all real numbers x .
Very interesting approach, thank you for responding to the problem and sharing your solution.
This is a problem I solved long back. This solution is totally different. Thanks for the nice solution.
For any real number n , the piecewise function f ( n ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ − x − n x − n 0 x + n − x + n if − 2 n k ≤ x < − 2 n k + n for any positive integer k if − 2 n k + n ≤ x < − 2 n k + 2 n for any positive integer k if x = 0 if 2 n k − 2 n < x ≤ 2 n k − n for any positive integer k if 2 n k − n < x ≤ 2 n k for any positive integer k has the property f ( f ( x ) ) = − x for all real numbers x .
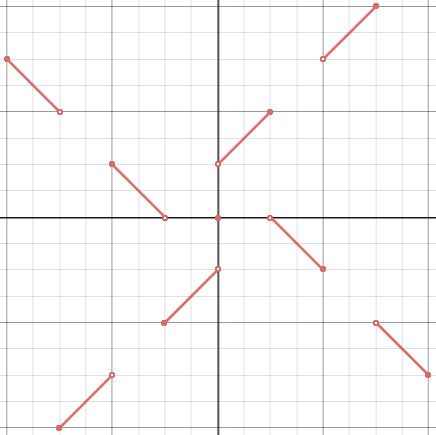
this is a good one! I love it.
I did the same!
This is Problem 20(b) of my book, 'Professor Higgins's Problem Collection', Oxford University Press, (2017). There are infinitely many solutions but each has infinitely many points of discontinuity.
Peter M. Higgins
Why we cannot put x = -x and then solve for f(f(-x)) = x ?
this is simple geography guys
We can construct infinitely many functions.
First note that f ( 0 ) must be 0 , or else the relation will not be satisfied for x = f ( 0 ) . Now partition the positive reals into pairs { x , y } . For each such pair, define
f ( x ) = y , f ( y ) = − x , f ( − x ) = − y , f ( − y ) = x or f ( x ) = − y , f ( − y ) = − x , f ( − x ) = y , f ( y ) = x
This satisfies the relation f ( f ( x ) ) = − x for all x ∈ R . This can be seen as: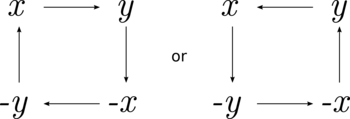
There are two choices for the function for each pair { x , y } . Since there are infinitely many such pairs in a given partition, there are infinitely many functions that satisfy f ( f ( x ) ) = − x .
Since we can partition the positive reals in infinitely many ways, and each partition gives infinitely many functions, there are infinitely many functions that satisfy f ( f ( x ) ) = − x .