Can they remain in equilibrium?
Two blocks are held against a vertical wall by applying a horizontal force, as shown in the diagram. The inner faces of the blocks (where the two blocks make contact) are rough, while all the other surfaces are frictionless. The gravity, of course, acts vertically downwards,
Is it possible for these blocks to remain in equilibrium?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Won't the other block exert a friction on the block against the wall?
What about the friction from the other block?
Log in to reply
If we look at the two blocks as one system, then what are the external forces acting on the system? Which of these forces are in the vertical direction?
There's no friction because it's the block against the wall that's exerting the normal force, isn't it?
If there are no other forces, the blocks will fall together? And if there is air-resistance, the normal forces will generate friction, keeping the blocks in equilibrium with each other?
Log in to reply
It is not air resistance that keeps the blocks in the equilibrium. Won't the air resistance come into play when the blocks are in motion?
Just because the surface is smith it does not mean the coefficient of friction is zero. In fact friction may be very high with polished surfaces
Log in to reply
Smooth not smith
Log in to reply
Agreed, that is why the question has mentioned that the wall is frictionless.
I understand that the horizontal opposing forces will not be able to resist the force of gravity acting perpendicularly in a downwards direction. My problem is more that because the wall is unable to move downwards (my understanding of a wall is that it is in contact with the ground) the only block able to move downwards would be the middle block (which has one friction surface and one frictionless) . If therefore as the answer suggests that this system cannot be equilibrium it implies that the middle block must be moving downwards which won't happen because one of its surfaces is a friction surface with the outer block. Am I incorrect in assuming that the middle block would only slide downwards if both of its surfaces were frictionless? If the innermost surface were not by definition a wall and could move downwards I would readily agree that the system could not remain in equilibrium but if we assume (as we do with walls) that they are immobile will the system remain in equilibrium?
Question... if the wall did not exist and there was no friction from the air and a constant force behind the blocks would they drop straight down? Of course not. I'm not sure they would even dro. A bullet doesn't drop until the energy that propels it dissipates and gravity then can affect it.
So why should it be different when a wall is there? Here the horizontal force is constant. The horizontal forces will exceed the ability of gravity to act on it until it weakens below a threshold. Because it comes from both directions does not nullify it but strengthens it.
This seems to have some merit. Not saying it's correct yet but it feels right.
Here's a logical explanation:Let us assume that coefficient of friction between blocks is as large such that the two blocks behave like a single body with friction as an internal force. This body is being pulled by gravitational force in downward direction and a force is being applied in horizontal direction. Hence it cannot remain in equilibrium.
I've just discovered Brilliant and love it. But this question is misleading and might put a lot of students off physics. In some idealised mathematical universe in which surfaces can be truly vertical and flat, the given solution would be true. But in the real world, surfaces have imperfections, and tiny ridges pointing in different directions. Therefore normal forces need not act entirely horizontally. Anyone knows that in the real world, you can press hard against the block and it will stay up, in equilibrium. Some of the normal forces will have a vertical component, and ultimately will push down against the earth beneath the wall. So this question may be answered "correctly" by people who learn physics unthinkingly line-by-line from a book, but incorrectly by people who think about it. I think it should be removed.
Log in to reply
It is not the vertical component of normal that keeps the block in the equilibrium in the real world. The word "normal" itself mean perpendicular to the surface. So, the normal must be horizontal in this case even if the wall is rough.
I think what you are talking about is the "contact force" that has two components, Normal reaction and friction force. It is true that we can not have a perfectly frictionless surface, in reality, however the question explicitly states it to assume the wall to be smooth.
So, the question is if the wall is indeed smooth (hypothetically), can these blocks remain in the equilibrium? As the question has stated all the conditions/assumptions, I don't think there is any ambiguity left in the problem.
Log in to reply
Hi Rohit, thanks for your reply.
Since you state the surface is rough, that to me would mean that (at some microscopic level) it is bumpy, so not entirely vertical, so at this level the normal would have vertical components.
You are being rigid about "normal" as if it's a constant well-defined vector. It can vary over the surface! This is what happens in the real world. Unless you make it clear that you're not asking a problem about the real world, but about a non-existent platonic world, I still don't like your question, sorry.
(I really like many of your other questions though! Eg the one about which container will fill first.)
Here's an analogy: suppose I put up a question about standing a pencil perfectly vertically on its perfectly sharp tip on a perfectly flat table, and mark "it will stand" as the correct answer and "it will fall over" as wrong. Don't you think that would be silly?
Log in to reply
@Richard Thomas – Ok, if you say that the normal have two components, then how would you define friction? Isn't it the tangential component of the contact force?
Log in to reply
@Rohit Gupta – You're trying to use the textbooks again....the model of friction there is an approximation, true at the macro- but not micro- level. The approximation is normally good, but in this circumstance its slight inaccuracy gives the wrong answer, as you can see by holding 2 blocks against a polished mirror!
Maybe my explanation is simplified. but if we put enough (really big) force on a block against a ice wall, which is the closest I know for small friction, it will fall? I doubt it. I am sorry, but I am an engineer, not a physicist.
Log in to reply
@Myrto Ananida – Think it in this way, smoother the wall, greater the force you will have to apply to keep them in the equilibrium. If the wall is perfectly smooth means zero friction, you will require an infinite force, which is not possible.
The problem did not state that the thought experiment took place inside Earth's gravity well. In zero gravity, equilibrium is possible. The whole thing relies on finding zero friction solids though- rocking horse dung comes to mind
What if the friction acts on the wall and surface between the blocks are smooth? Will the blocks achieve the equilibrium as now they have a net upward external force?
The question asks "Is it POSSIBLE... YES also has the caveat "If sufficient horizontal force is applied". The scenario starts by explaining that the blocks are already held, it's not explained that you have to place them, and then apply the force. Too much ambiguity.
Not enough information in the original problem. Nothing was mentioned about gravity. The problem is flawed.
Log in to reply
It's obvious ...
Log in to reply
Gravity should be assumed present unless and until stated otherwise.
The answer is YES UNLESS there is a vertical force. Any vertical force should have been included in the problem.
There are two force arrows marked. The smaller one is providing lift so the gravity argument is inconclusive. Equilibrium requires the vertical component of the diagonal force to precisely counteract gravity, together with sufficient horizontal force to resist the horizontal component of diagonal force.
Log in to reply
I think the smaller arrow was really intended to point to the interface with friction, not to show a force vector. The head of the arrow should have been at the junction of the blocks. If I am correct, there is no force implied in this diagram other than the blue arrow! Gravity, too, must be assumed absent; otherwise there would have been a force vector shown for it.
For me, the issue is whether the normal force is absolutely normal. Any infinitesimal deviation from normal would produce a finite resultant force parallel to the wall, and the blocks would move. This problem, with no other constraints denoted, seems to imply a perfectly 'normal' Force. Thus it is in unstable equilibrium..
Log in to reply
Normal means perpendicular to the surface, even if the wall is rough, still the normal will be perpendicular to the surface. The tangential component is called friction which is zero according to the problem.
Agreed, there is a problem I have with some of these questions: Hidden unstated assumptions. This question should be changed or tossed out, as the unknown questionaer assumes the problem in on the Earth or some other body.
Let us do this stepwise. For the rightmost block to be in equilibrium, friction must be UPWARD so as the balance its weight. This friction is due to the block on the left. By Newton's third law, an equal and OPPOSITE frictional force acts on the block on the left. Hence, the frictional force on the left block must be DOWNWARD. But this would only add to the weight of the block instead of cancelling it. There is no other force which can balance these two forces. Hence, it must accelerate downward. So the system can never be in equilibrium.
Suppose a hand exerts the horizontal force (blue arrow) on the block. If the surface between the hand and the block is also rough ( the wall is still frictionless), then can the blocks achieve equilibrium?
The blocks ARE being held, that is the stated in the question. What changes that state to a downward one, if all remains the same?
Log in to reply
Being "held" and being "held against" are different things ... in this case they are being "held against" the wall, which means the force of holding is towards the wall, unlike the general case, where to simply "hold" something is assumed against gravity.
I do not agree with the solution. Sufficient pressure to hold the blocks in place suggests enough lateral force to counter gravity's downward pull. If this suggessted solution were true, clamps would not work.
Right, the only external force on the block in the vertical direction is their weight downwards, so they will move downwards.
Gravity will pull the two blocks downwards. There is no force to oppose it. In particular, since the frictional forces between the two blocks are equal and opposite, they will have no effect on the combined momentum of the blocks. The best the friction can do is keep the blocks falling down together.
In the real world, if you actually held the blocks against the wall with your hand, you would indeed stop them falling down (essentially creating an equilibrium). But in this scenario, the force you exert with your hand has a vertical component (friction) - unlike in this problem, where it's just a horizontal force.
The wording of this problem is imprecise. The nature of the question seems to imply that one is asking whether or not a force, applied horizontally, will be able to maintain a constant position of the blocks relative to the wall.
It is vague to ask if the blocks maintain equilibrium. One could argue that the blocks indeed maintain their equilibrium as they slide down the wall.
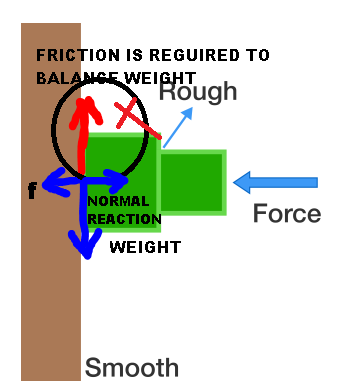
Consider only the block nearest the wall. There are three forces acting on it: the normal force from the other block, another normal force from the wall, and the force of gravity. The normal forces are perfectly horizontal and can cancel each other out but the gravitational force going perfectly downward has no such partner as a smooth wall cannot cause a frictional force. This unbalanced gravitational force will cause the block to accelerate away from equilibrium.