Can we call this Reuleaux Square?
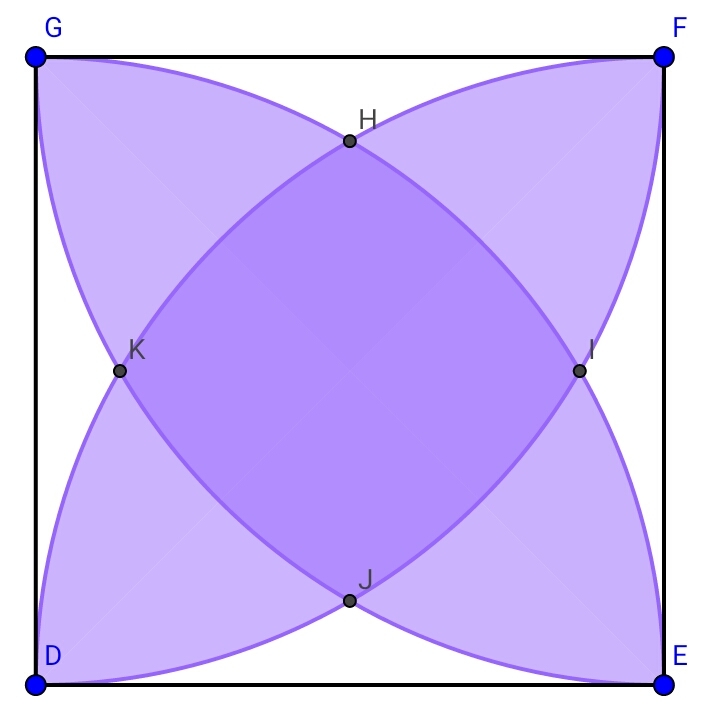
D E F G is a square. Four quarter circles are drawn with D , E , F , and G as the center and D G , E D , F E , and G F as the radius. If D E = 4 cm , find the area of white region ( in cm 2 ).
The answer is in the form a − c b π − d e , where a , b , c , d , e are positive integers, g cd ( b , c ) = 1 , and e isnt' divisible by the square of a prime. Find a + b + c + d + e .
Bonus: 1 . Find the area of the purple region
2 . If you see in the middle of the figure, you'll find a four-sided shape, named H I J K . Find its area!
3 . If D E = n cm , find the area of the white region and the area of purple region in term of n
Try another problem on my set! Let's Practice
The answer is 118.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Yeah. It supposed to be all different. I forgot to mention it.. Sorry.
Wow, such a beautiful solution. Upvoted!
Log in to reply
Thank you, Fidel!
Log in to reply
By the way, what motivates you to make such solution? This kind of problem require a diligent person to solve.
Log in to reply
@Fidel Simanjuntak – I've thought about the solution for the "Reuleaux square" area a couple years ago, when I was looking to a similar drawing in an apartment's floor. So, this to me was like extending my wondering from a couple years ago! :)
Besides, I like to be always didactic!
Log in to reply
@Guilherme Niedu – Wow.. Such a nice coincidence.. Hehehe
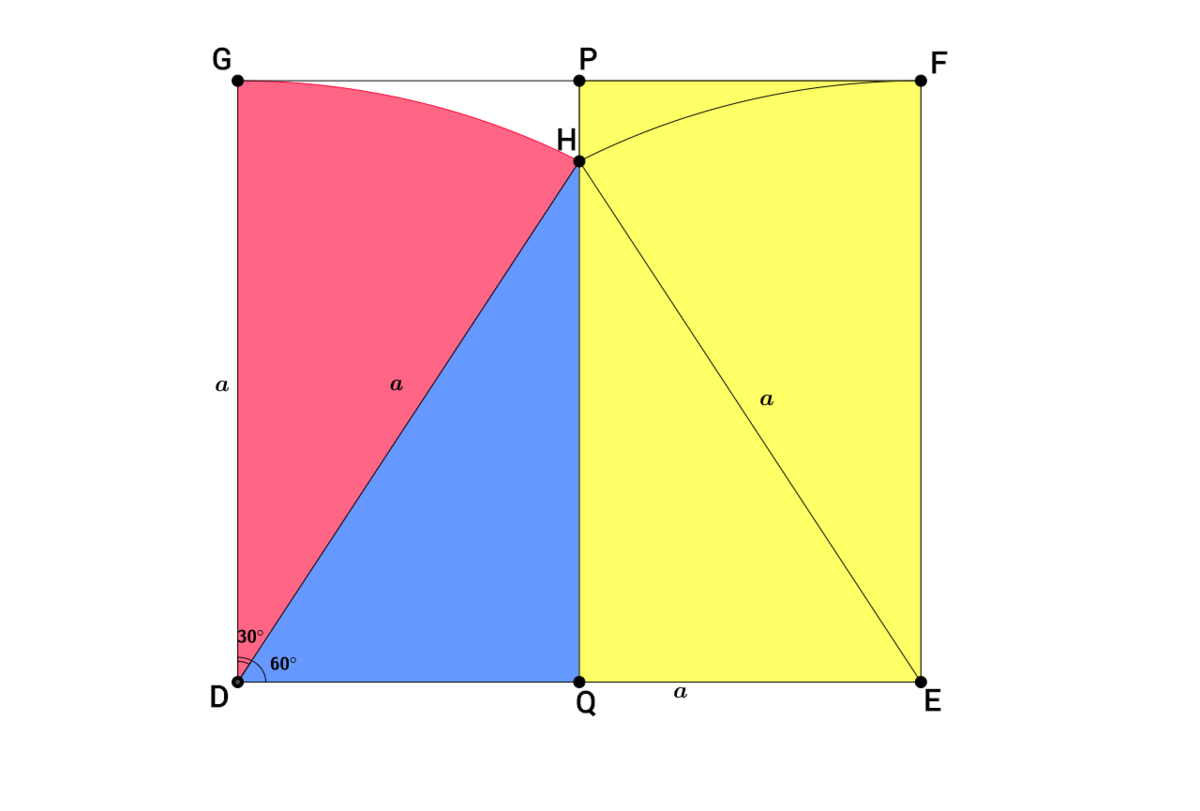
The area of the required region is equal to 8 times the area of the white region in the above figure
From the above figure it is clear that ,
Area of the white region = Area of yellow region − (Area of blue region+Area of red region)
Now Δ DEH is equilateral as all sides equals a
⟹ ∠ H D E = 6 0 ∘
⟹ ∠ G D H = 3 0 ∘ ∠ G D E = 9 0 ∘ as DEFG is a square
Area of yellow region = 2 Area of square = 2 a 2
Area of red region = Area of sector DHG = a 2 ⋅ 1 2 π Area of sector = r 2 2 θ where r is the radius and θ the angle of the sector in radian
Area of the blue region = 2 Area of Δ D E H = 8 3 ⋅ a 2 Area of equilateral triangle with side a = 4 3 ⋅ a 2
Thus we have,
Area of white region = 2 a 2 − ( a 2 ⋅ 1 2 π + 8 3 ⋅ a 2 ) = 2 a 2 ( 1 − 6 π − 4 3 )
Area of required region = 8 × Area of white region = 2 8 a 2 ( 1 − 6 π − 4 3 )
a = 4 in the above problem ,
⟹ Area of required region ⟹ a + b + c + d + e = 6 4 ( 1 − 6 π − 4 3 ) = 6 4 − 3 3 2 π − 1 6 3 = 6 4 + 3 2 + 3 + 1 6 + 3 = 1 1 8
Why is it only for an odd number of sides ?
Log in to reply
You can review above link by copy it and paste in any searching engine as google.
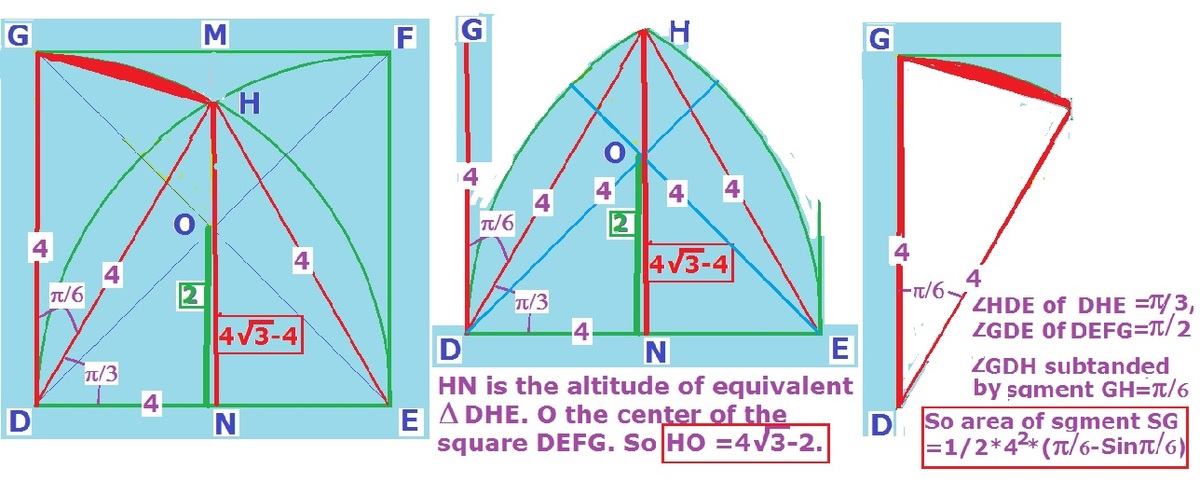
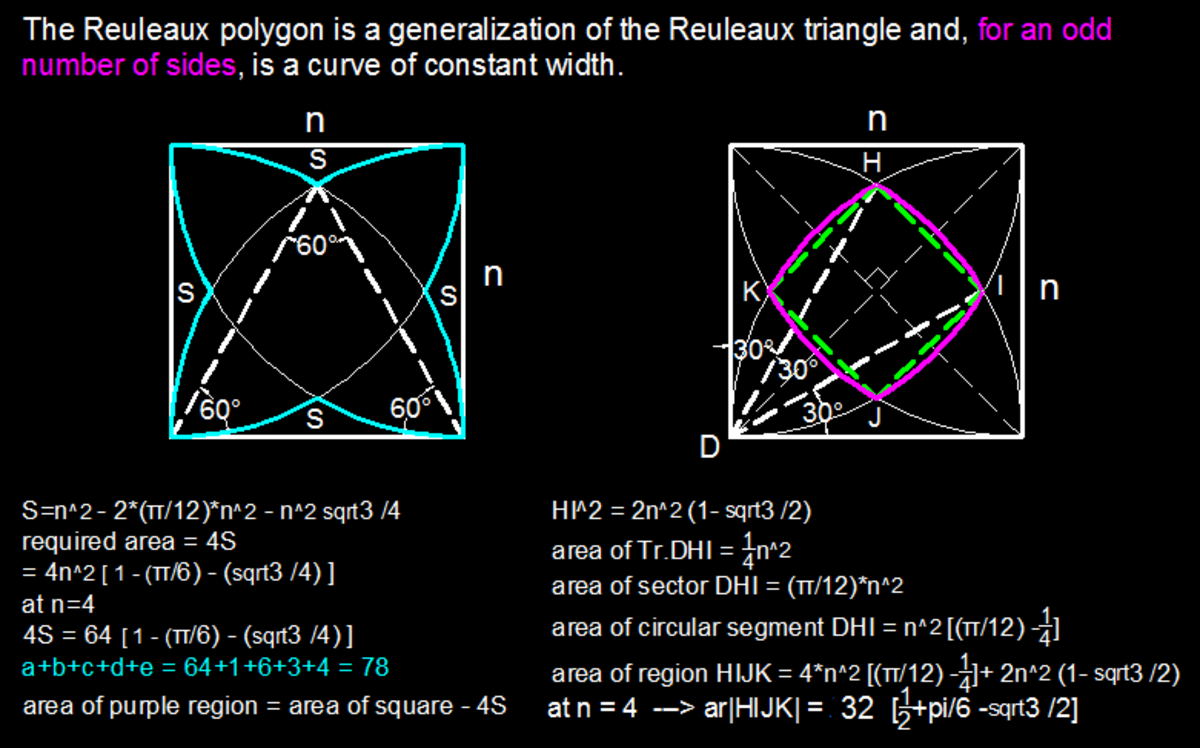
I'll do it all in terms of n . First of all, it is important to note that ∠ H D I = ∠ K E H = ∠ J F K = ∠ I G J = 3 0 o . Denoting J K as x , by cosine law:
x 2 = n 2 + n 2 − 2 n 2 ⋅ cos ( 3 0 o )
x 2 = n 2 ⋅ ( 2 − 3 )
Area H I J K is the area of a square of side x plus 4 areas of circular segments, with angle 3 0 o and radius n :
A H I J K = x 2 + 4 ⋅ ( 1 2 π n 2 − A Δ D H I )
Calculating A Δ D H I by sine law and substituting x 2 :
A H I J K = n 2 ⋅ ( 2 − 3 ) + 4 ⋅ ( 1 2 π n 2 − 4 n 2 )
A H I J K = n 2 ⋅ ( 1 + 3 π − 3 )
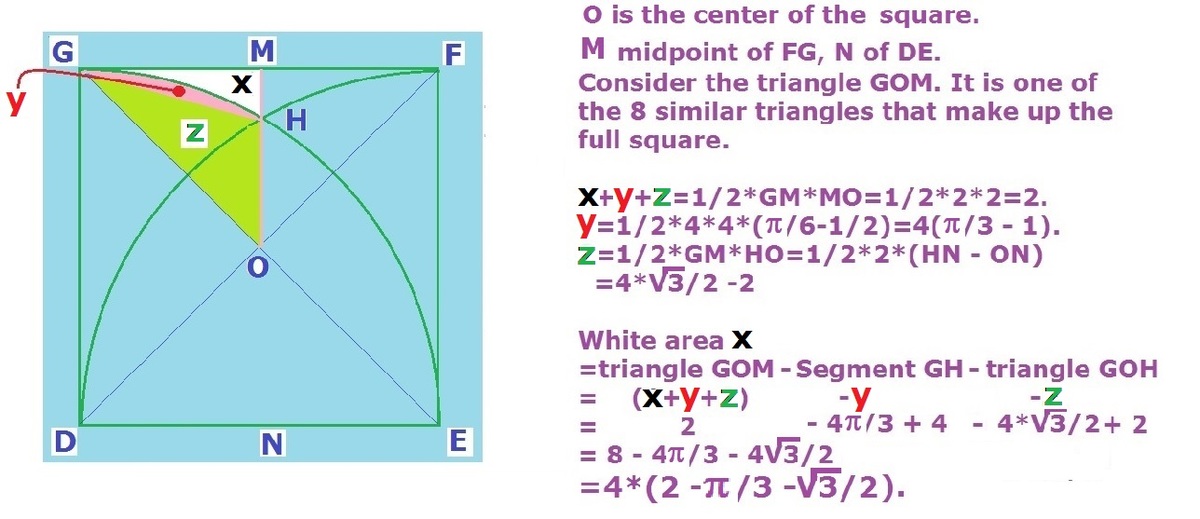
now, to calculate A D K H F I J , i.e., the area of the slit-looking part:
A D K H F I J = n 2 − 2 ⋅ ( n 2 − 4 π n 2 )
A D K H F I J = n 2 ( 2 π − 1 )
The area of each corner of the slit will be:
A D J K = 2 1 ( A D K H F I J − A H I J K )
A D J K = 2 1 [ n 2 ( 2 π − 1 ) − n 2 ⋅ ( 1 + 3 π − 3 ) ]
A D J K = 2 1 n 2 ⋅ ( 6 π − 2 + 3 )
The whole purple area will then be:
A P U R P L E = A H I J K + 4 ⋅ A D J K
A P U R P L E = n 2 ⋅ ( 1 + 3 π − 3 ) + 4 ⋅ 2 1 n 2 ⋅ ( 6 π − 2 + 3 )
A P U R P L E = n 2 ⋅ ( 3 2 π + 3 − 3 )
White area will be:
A W H I T E = n 2 − A P U R P L E
A W H I T E = n 2 − n 2 ⋅ ( 3 2 π + 3 − 3 )
A W H I T E = n 2 ( 4 − 3 2 π − 3 )
For n = 4 this leads to:
A W H I T E = 1 6 ( 4 − 3 2 π − 3 )
A W H I T E = 3 2 ( 2 − 3 1 π − 2 1 3 )
Which would lead to a = 3 2 , b = 2 , c = 3 , d = 2 , e = 3 , a + b + c + d + e = 4 2
However, this is not the correct answer according to the problem. I am assuming that a , b , c , d and e must be all different. Re-writing A W H I T E leads to:
A W H I T E = 6 4 ( 1 − 6 1 π − 4 1 3 )
So:
a = 6 4 , b = 1 , c = 6 , d = 4 , e = 3 , a + b + c + d + e = 7 8