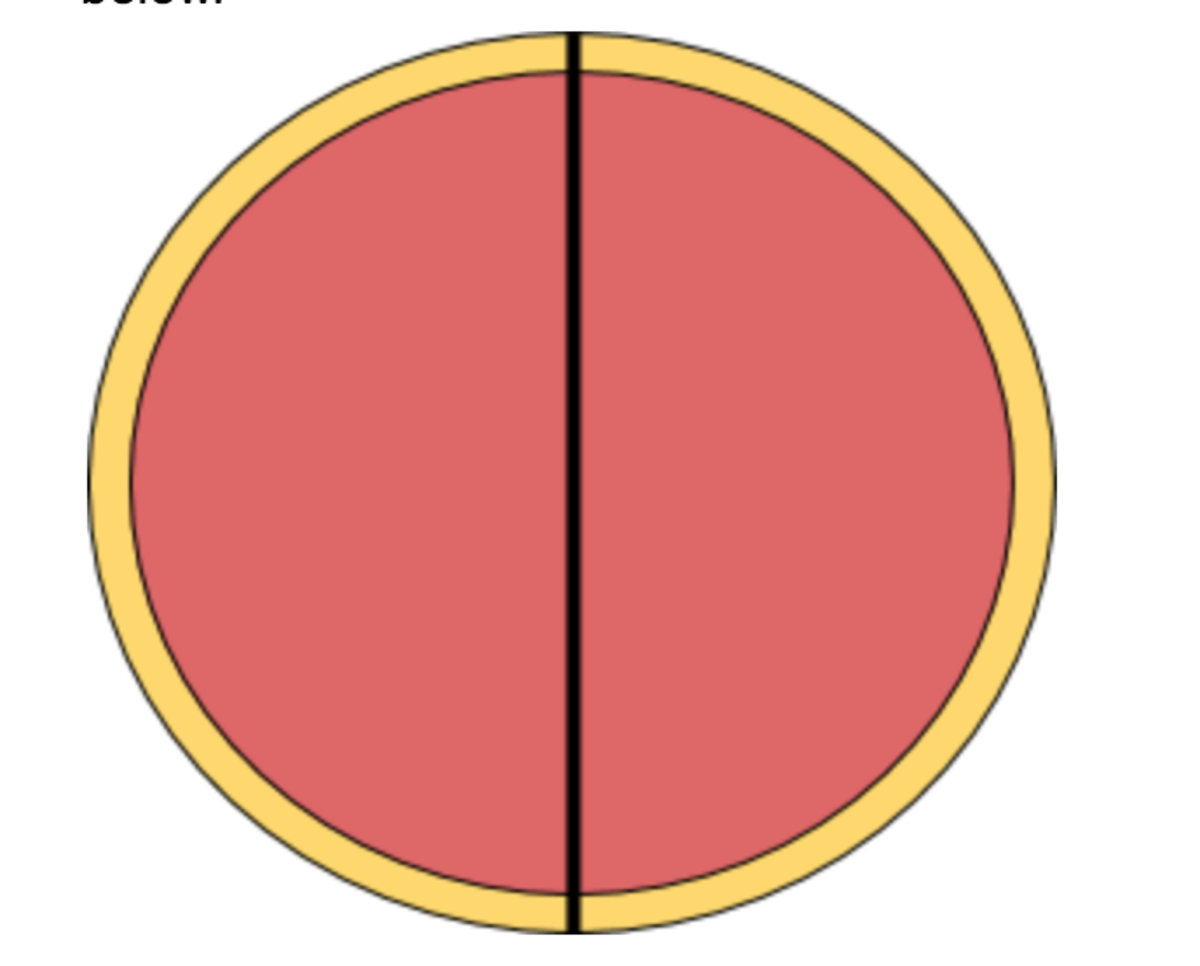
Can we have equal area and equal crust?
I cut a pizza in the shape of a circular arc such that there are 2 pieces of equal area.
Is it possible that these 2 pieces have the same amount of crust on the circumference?
Assume the crust is 1-dimensional, i.e. it's just the circumference of the pizza with no area.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
What if the radius of the arc is infinite? Or can that be ruled out?
Log in to reply
An arc with an infinite radius would be a straight line, which I believe can be ruled out since the problem said the cut is a circular arc.
Log in to reply
It is a question only in the limit approaching infinite radius. The answer seemed too obvious except for the infinite limit, so I answered that you could do it on those grounds. The infinite limit is a basic tool used in math and should really not be assumed to be out of bounds. Yes, a circular arc approaches a straight line in the infinite limit, this should be explicitly excluded if not allowed in a math puzzle, IMHO. It seemed to be the point of the question to me, until it was marked incorrect.
Log in to reply
@Jason Sackett – Except for you are actually making the slice, not a theoretical slice but an actual one....are you able to make physically an arc of infinite radius...no.
Log in to reply
@Jerry Duncan – @Jerry Duncan Then where is my slice of pizza? Oh, you weren't being literal. The question is 'Can we have equal area and equal crust?' with an illustration of a circle and a question concerning area and perimeter where the answer is totally obvious, except for thinking of the case in the infinite limit. I think this question is poorly worded and should be fixed or removed.
Log in to reply
@Jason Sackett – Please check the Challenge Master note to Tomáš Žilínek's answer - a circle of infinite radius is a half-plane, not a circle.
What if arc is a complete circle? That is the two points of the arc meet at a point on the circumference i.e. the arc is complete circle internally touching the larger circle having radius^2=half of big circle radius^2.
Log in to reply
Then the two pieces would not have the same amount of crust.
If the area of the pieces is equal, "I cut a pizza ... such that there are 2 pieces of equal area.", isn't that the same as saying that they have the same amount of crust?
Ah! It's the caveat that does it: Assume the crust is 1-dimensional, i.e. it's just the circumference of the pizza with no area.
Man, a 1 dimensional pizza would be the biggest rip-off in the history of food. I'll sell you a one-dimensional pizza! Here I just gave it to you, what do you mean you can't see it? It has no mass and no area, so you can literally put an infinite number of them into an infinitely small space. That would be the ideal basis for a global food delivery empire!
It would be like selling an individual electron. 😀
Except of using the arc of a cycle with infinite radius, which is indeed a straight line hence the diameter
Log in to reply
A straight line cut can be ruled out since the problem states that the cut is a circular arc.
Log in to reply
An aberrant arc can have diameter infinite!
Log in to reply
@Luca Codeluppi – Check the Challenge Master note on Tomáš Žilínek's solution - as it points out, a "circle of infinite radius" isn't a circle, it's a half-plane.
What will happen if the crust aren't uniformly distributed?
Log in to reply
If it's not 1-dimensional (as given) you can add as much crust as you need to on one side or the other to make the problem work.
Why not have the circular arc have a radius of curvature of infinity? Then it would have equal perimeter
Log in to reply
An arc with an infinite radius would be a straight line, which I believe can be ruled out since the problem said the cut is a circular arc.
As by many people already written, to have the same amount of crust the endpoints of the circular arc would have to be on the circle diameter and to have the same areas the boundary would have to be straight line. !!!BUT!!!
What if the circle creating the arc on the pizza was infinitely large. The roundness of the circle would be "unimportant" or "negligable" and the boundary would be aaaaaaaaaalmost strainght line. :D I know that circle any big cannot divide the pizza to, exactly, 2 equal areas so while disproving my suggestion please dont use this argument. :D
Moderator note:
A "circle of infinite radius" isn't a circle. It is a half-plane.
Just because something can be obtained as the limit of items in category X, doesn't mean that the limit must be in category X. For example,
- 0 = lim x → 0 + x is not a positive number.
- ∞ = lim x → ∞ x is not a real number.
- π = limit of 3 , 3 . 1 , 3 . 1 4 , 3 . 1 4 1 , … is not a rational number.
- Limit of the non-empty sets ( 0 , x ) is not a non-empty set.
An operation / property has closure if performance of the operation always returns an element of the set. For example,
- the set of positive integers is closed under finite addition.
- the set of positive integers is not closed under infinite addition.
- the set of open sets is closed under finite intersection.
- the set of open sets is not closed under infinite intersection.
Saying aaaaaaaaaalmost and saying exactly aren't logically equivalent in this context for the very reason that it specifies it distinctly as a circular arc. No circular arc is ever a straight line. Simple as that.
Log in to reply
"No circular arc is ever a straight line." - And why is that true? Nowhere in the question it says that the circle cannot be of infinite radius. Alternatively instead of radius we can define a circle in terms of its curvature. A curve with constant curvature is a circle. We can think of a curve with curvature of constant value 0, which makes it a circle and also a line. You might also like to read about Generalised circle - https://en.wikipedia.org/wiki/Generalised_circle
Log in to reply
Because 'infinite radius' is not actually a radius. Infinity is only defined as a limit that something approaches. When you are creating a counterexample to this problem, you must specify a number for the radius of the circle, and since infinity is not a number, so such number exists.
Log in to reply
@Alex Li – That's why I defined the circle in terms of its curvature. This question is highly based on what we define a circle is. What I said is accurate in Inversive Geometry. And please if you are making statements like 'you must specify a number for the radius of the circle' provide a proof of that statement.
Log in to reply
@Shubham Khandalkar – A circle is a well-defined object. The wiki article is not trying to say that circles can be lines. It is defining a new object, a "Generalized circle". The article is needed for precisely the reason that, without it, you would not be able to have a generalized circle as that object is not a circle. A generalized circle is NOT a circle, in fact, it is defined as "A straight line or a circle". I admit that this is pretty confusing because they are both called circles, but they are different ideas.
As for the proof of my statement: this statement can be false iff there exists a counterexample. In order to provide a counterexample, you would have to specify a circle, so somehow you would also specify the radius. As I said above, you cannot specify a circle with infinite radius.
I thought this also :) But an arc is not a straight line
I agree. As the radius of the arc tends to infinity, the difference between the amount of crust on each side of the pizza tends to 0.
The question is "is it possible...". An infinitely large circle creates a straight line division, not aaalmost a line.
Circles aren't "infinitely large".
Mathematically a straight line segment is a special case of a circular arc. Admitting this makes it a trick question, but that doesn't change the fact the correct answer is "yes".
Log in to reply
Those were my thoughts as well..
Log in to reply
If you have not yet, please check the Challenge Master note to this problem.
Log in to reply
@Jason Dyer – I did read the the Challenge Master note, and while I'm not at a level of knowledge to disagree, I was not entirely satisfied by it.
For me, this question seemed too obvious, leading me to interpret the "real" question as "Does the author count the edge case of a straight line as valid?"
Given that the question contained a disambiguation on the crust being 1 dimensional but made no mention of limiting the radius of the arc segment, and since guessing no would make the "real" answer the same as the "too simple" answer, I guessed yes.
I still agree with other commenter who suggested the question could use further disambiguation.
Log in to reply
@Adam Wilkinson – Most people do, in fact, think of a "circlular arc" as curved - trying to imagine extreme rules violations is fairly unusual (although they do like to write comments). However, if an extreme rules violation is invalid, it does not need any clarification, and the clarification can in fact confuse more than help. Here, this is because most people do go in with the assumption it is curved, so having some specific note about it can actually cause them to out-think themselves and double back. We've seen this several times from data where a hint actually makes the solve rate go down.
So challenge master explain please in the same logic how a collection of infinite points form a line , or line does not constitute of points ?
Log in to reply
Indeed, an infinite collection of points is a line. That is how a line is defined. It's not taking the "limit" of items in a category, because it's defined specifically as being the category.
Related to the analogy, though: you can't assume that if you taking an infinite number of line segments collinear and placed in a constant fashion in both directions, you have an "infinite line segment". You don't; you have a line. Even though the word base is similar, "line segments" and "lines" are very different things.
I think that all the controversy itself concerning this problem and its questionable posing is enough to point out that the question should be clarified and rewritten, or abandoned. In the evaluation of assessment test questions, when success on a question has poor correlation with success overall, the question is re-written or discarded.
Log in to reply
As another problem intro on this site states:
"Key Strategies for the AMC Often, it's useful to think about an extreme case of a problem. Then, you can check if that extreme case is possible, and if not, how close you can get."
Curvature = 0 is an extreme case that is not ruled out in the question posed here.
@Jason Sackett If people are getting a problem wrong, that doesn't mean we necessarily accommodate every possible hint. We have found historically that adding "hint text" can actually drop the solve rate.
This is one case where that's quite possible. That's because the majority of solvers do not think of a line as an arc (and as pointed out in the challenge master note, it is not). So a hint and extra text can potentially cause them to second-guess themselves.
It's ok for a subset of people to get something wrong - it's a learning experience.
If the cut has to be equal then the slicing should be done along the diameter and one piece should fit into another!!!
The arc belongs to both pieces. Therefore if both pieces have the same perimeter, then outer boundary of each piece has to be half circumference. In that case only a diameter can divide the circle into two parts of equal areas.
To have equal crust, the cut must begin on either side of the diameter of the pie. The only way to ensure that the slices have the same area is to cut straight across. However, as the cut is circular, one slice will always be larger than the other, making it impossible to achieve this kind of task.
For two pieces to have equal circumference(crust); they need to cut the pizza with end points of a diameter as the start and end points. But in such a situation as the cut is in shape of a circular arc, one of the pieces will have more area. Hence, the two pieces cannot have equal area and crust simultaneously.
In any pizza I have yet to see a completely uniform crust no matter which way it's cut
The only way the crust can be the same is when the line is straight across the circle as shown below.
(Obviously, it can be drawn another way)
However, if we start to arc the line, one side always gets more crust. Even if we just arc the line a little we can start to see one side gets the most crust.
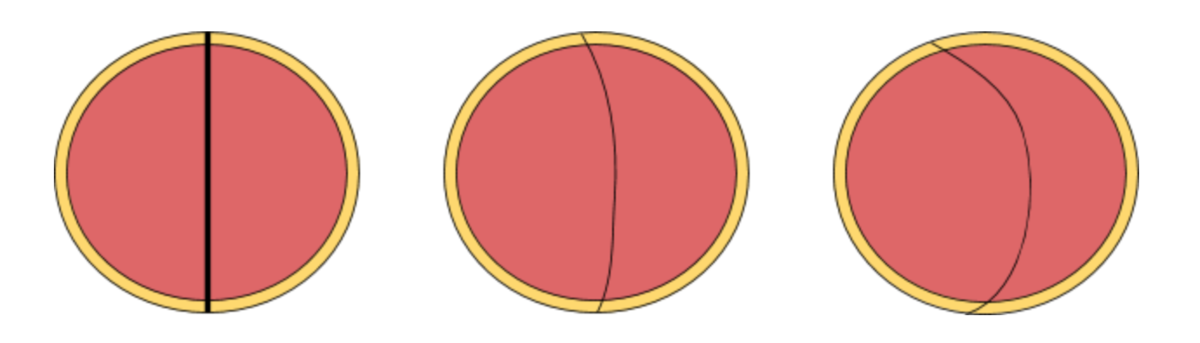
You can see that the left line is getting more crust. This shows if the line is arched, it's impossible for both sides to have the same amount of crust.
Arc radius = infinity. This was not ruled out in the question
Log in to reply
That is true, but we can assume that this is a rational pizza with finite side lengths. However, if the pizza were to have an infinite circumference, it would still be less because some infinities are smaller than others so it still is not possible.
If i draw the same arc, and I rotate it 180° from the center, i would have 4 equally shapes and the center, the left and right shapes are the same, also the top and bottom shapes are the same, so the sum of the 2 shapes must have the same area as the center, and because the center doesnt have crust, the crust of the 2 starting shapes are not equal.
If I have a circle with an infinitely long diameter I could actually slice the pizza in two equal pieces each having the same amount of crust.
Log in to reply
Actually if is infinitely long the diameter, any straight line vou cut from the pizza, will have infinite crust.
For the two pieces to have the same amount of crust, the starting point and ending point of the circular cut must be endpoints of the diameter of the pizza, and if this is the case, the piece inside the bulge of the circular cut will have more area than the other piece. Therefore, by indirect proof, it is not possible for two pieces of equal area cut by a circular cut to have the same amount of crust.