Can you find a formula for this?
⎩ ⎪ ⎨ ⎪ ⎧ 1 + 2 + 3 + ⋯ + ( n − 1 ) + n = 2 n ( n + 1 ) 1 2 + 2 2 + 3 3 + ⋯ + ( n − 1 ) 2 + n 2 = 6 n ( n + 1 ) ( 2 n + 1 )
Using the well-known identities for the sum of first n positive integers and sum of first n squares above, find the identity for the following sum:
1 ( n ) + 2 ( n − 1 ) + 3 ( n − 2 ) + ⋯ + ( n − 1 ) ( 2 ) + n ( 1 )
If the answer can be expressed as d ( n + a ) ( n + b ) ( n + c ) , find a + b + c + d .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Excellent visualization
I wish I thought of it that way! This seems far more clever than my pitiful re-arrangement of terms.
In summation notations, we have k = 1 ∑ n k = 2 n ( n + 1 ) , k = 1 ∑ n k 2 = 6 n ( n + 1 ) ( 2 n + 1 ) , and
S = 1 ( n ) + 2 ( n − 1 ) + 3 ( n − 2 ) + ⋯ + ( n − 1 ) ( 2 ) + n ( 1 ) = k = 1 ∑ n k ( n + 1 − k ) = k = 1 ∑ n ( ( n + 1 ) k − k 2 ) = ( n + 1 ) k = 1 ∑ n k − k = 1 ∑ n k 2 = 2 ( n + 1 ) n ( n + 1 ) − 6 n ( n + 1 ) ( 2 n + 1 ) = 6 n ( n + 1 ) ⋅ ( 3 ( n + 1 ) − ( 2 n + 1 ) ) = 6 n ( n + 1 ) ( n + 2 )
Therefore a + b + c + d = 0 + 1 + 2 + 6 = 9 .
1 × n + 2 × ( n − 1 ) + 3 × ( n − 2 ) + . . . + ( n − 1 ) × 2 + n × 1 can be rewritten as:
1 + ( 1 + 2 ) + ( 1 + 2 + 3 ) + ( 1 + 2 + 3 + 4 ) + . . . + ( 1 + 2 + 3 + . . . + n )
The expression above has (n) 1's, (n-1) 2's, (n-2) 3's, ... , and 1 n'(s). Therefore it is equivalent to the sum of the first n triangle numbers. The formula for the x t h triangle number is the first formula,
1 + 2 + 3 + 4 + . . . + x = 2 1 ( x 2 + x ) , and so we plug in 1, 2, 3, all the way to n for x, and then sum it all up.
So the expression is
2 1 [ ( 1 2 + 2 2 + 3 2 + . . . + n 2 ) + ( 1 + 2 + 3 + . . . + n ) ] = 2 1 [ 2 n ( n + 1 ) + 6 n ( n + 1 ) ( 2 n + 1 ) ] ,
and then through some simplification we arrive at the formula,
1 × n + 2 × ( n − 1 ) + 3 × ( n − 2 ) + . . . + ( n − 1 ) × 2 + n × 1 = 6 n ( n + 1 ) ( n + 2 ) ⇒ a = 0 , b = 1 , c = 2 , d = 6
a + b + c + d = 0 + 1 + 2 + 6 = 9 .
Very nice. I wonder if there's a geometric "proof without words" (the sum of triangular numbers is a tetrahedral number). Also, these numbers are one of the diagonals of Pascal's triangle.
Log in to reply
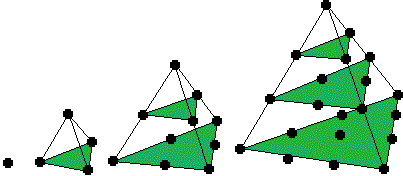
Each layer in a regular tetrahedron is the next triangular number, so the sum of triangular numbers is a tetrahedral number.
Log in to reply
Ah, sorry, I wasn't clear in my comment there - I meant a wordless way of proving the formula in the question.
Log in to reply
@Chris Lewis – Oh, I see. Good question!
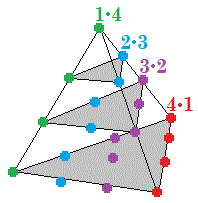
@Chris Lewis – Got one. The different terms represent the number of dots in diagonal slices of a regular tetrahedron, and the following picture shows the specific case for n = 4 :
The series can be expressed as
T r = r ( n − r + 1 )
T r = ( n + 1 ) r − r 2
∑ r = 1 n T r = ( n + 1 ) ∑ r = 1 n r − ∑ r = 1 n r 2
S = ( n + 1 ) 2 n ( n + 1 ) − 6 n ( n + 1 ) ( 2 n + 1 )
S = 6 n ( n + 1 ) ( n + 2 )
So, a = 0 , b = 1 , c = 2 and d = 6
So, a + b + c + d = 9
The different terms represent the number of dots in different diagonal slices of a regular tetrahedron, so the sum of the terms will be a tetrahedral number. The following picture shows the specific case for n = 4 :
Since the n th tetrahedral number is 6 n ( n + 1 ) ( n + 2 ) , that means a = 0 , b = 1 , c = 2 , d = 6 , and a + b + c + d = 9 .