Can You Guess This ?
a + b + c + d = 5
Find the minimum possible value of a 2 + 2 b 2 + 3 c 2 + 4 d 2
Details & Assumptions
- a , b , c , d ∈ Positive real no.s
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Cauchy is the best inequality ever
It should be ( 1 + 2 1 + 3 1 + 4 1 ) and not ( 1 2 + 2 1 2 + 3 1 2 + 4 1 2 )
The question is overrated
Did same!!
Log in to reply
Me too!!!!
Log in to reply
wow!! .....
Lagrange multipliers for g ( x 1 … n ) = k = 1 ∑ n x k − n 5 = 0 , f ( x 1 … n ) = k = 1 ∑ n k x k 2 give ∇ g = ( 1 , … , 1 ) , ∇ f = 2 ( x 1 , 2 x 2 , … , n x n ) and, for ∇ f = λ ∇ g , a single local extreme for x k = k c .
We can find the value of c by substituting back to the expression for g = 0 , as c = H n 5 , where H n = ∑ k = 1 n k 1 is the n -th harmonic number. We can guess that the answer is a minimum, since there must be one (the value of our continuous function f has a lower bound of 0, R + 2 is an open continuous space) and setting all but one of the variables x k to 0 points to a maximum instead (alternatively, by computing the Hessian of f and showing that it's positive definite). The answer is therefore ∑ k = 1 n H n 2 5 2 k = H n 2 5 = 1 2 in case n = 4 .
From Titu's Lemma; (a^2)/ 1+ (b^2)/ (1/2)+ (c^2)/ (1/3)+ (d^2)/ (1/4) will > or = (a+ b+ c+ d)^ 2/ (1+ (1/2)+ (1/3)+ (1/4)) but (a+ b+ c+ d)= 5 so, a^2+ 2 b^2+ 3 c^2+ 4*d^2 > or = (5)^2/ (25/ 12) = 12
We can also use weighted mean inequality
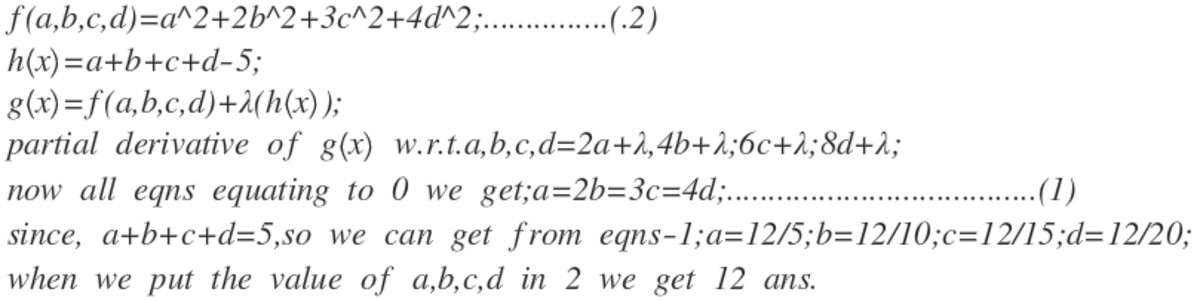
Using Cauchy Schwarz Inequality,
( 1 + 2 1 + 3 1 + 4 1 ) ( a 2 + 2 b 2 + 3 c 2 + 4 c 2 ) ≥ ( a + b + c + d ) 2
1 2 2 5 ( a 2 + 2 b 2 + 3 c 2 + 4 c 2 ) ≥ 5 2
( a 2 + 2 b 2 + 3 c 2 + 4 c 2 ) ≥ 1 2