A preview: Can you solve this?
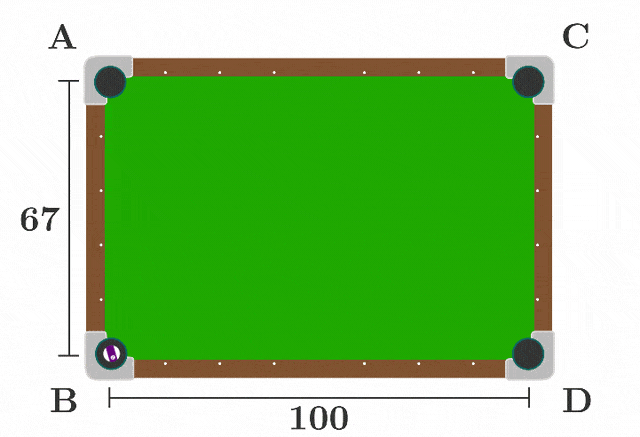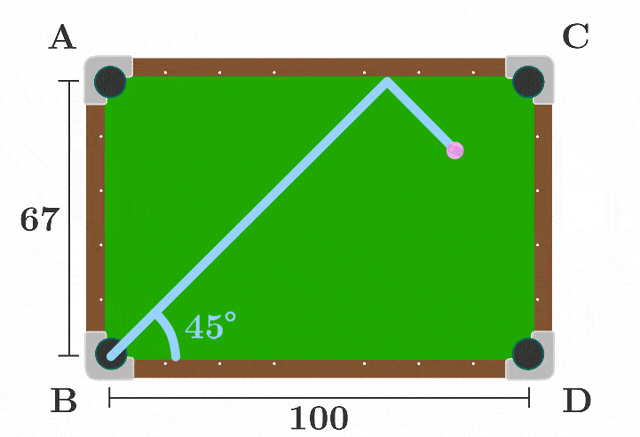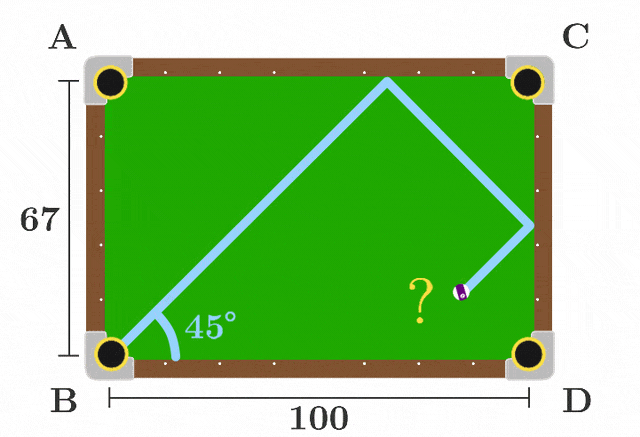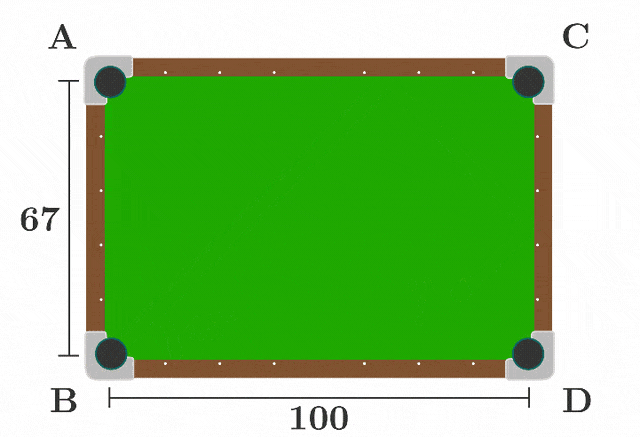
Which pocket will the ball end up in?
Assume that the ball is shot at a 45 degree angle directly from corner B of the table and that it will only land in a pocket if the center of the ball meets the corner of the pocket exactly . Model the ball as a point mass on a frictionless table.
This puzzle can be solved by carefully considering the path of the ball bounce-by-bounce, but there's also a beautiful shortcut that combines geometry and algebra to calculate the solution in <1 minute!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
A beautiful way to think about this!
Very elegant approach! If you enjoy the visualization of this problem and want to play around with it more, here's a tool that models the motion: https://phet.colorado.edu/en/simulation/proportion-playground
What if the angle was 30 instead of 45. The ball would never land in any pocket.. Right?
Log in to reply
Yes, because the ball would never be able to travel a rational distance both horizontally and vertically simultaneously.
Log in to reply
Only theoretically
Log in to reply
@Mohamed Aly – Since 3 is irrational, there is a definite answer here. If you are going to tell me that the pockets have a width, and so there is some margin for error, then we are talking a very different problem. For that matter, friction will have stopped the cue ball before it has crossed the length of the table 6 7 times!
Allow me to express my frustration at the labeling of the vertices! When labeling a rectangle, the points regularly go either clockwise or counter clockwise, not arbitrarily, as was done here. I made the mistake of not looking carefully at the drawing (my mistake), and looked at only A and B then continuing the pattern. I ended up with the correct answer on my paper "Lower right" but the wrong letter.
Followed the same number theory method here. :)
I spent ten minutes going bounce to bounce until I finally realized this.
Can you explain to me why it must travel the 67 table widths and 100 table heights? I understand the explanation but I was wondering how it worked specifically.
Log in to reply
Suppose the ball has travelled x table widths (a total horizontal distance of 1 0 0 x ) and y table heights (a total vertical distance of 6 7 y ) when it enters a pocket. Since the ball is alwaya travelling at 4 5 ∘ to the sides of the table, the horizontal and vertical distances it travels must always be equal. Thus 1 0 0 x = 6 7 y . The smallest values for x , y for which this is possible are x = 6 7 and y = 1 0 0 .
Log in to reply
Wow, thank you! It makes perfect sense now!
I like this answer because it's basically just reverse engineering. Looking first at where the ball can land (the pockets) and what conditions have to be true for it to be there and then looking at what happens. Nice calculation.
Correct me if I'm wrong .
I think since the base is an even integer thus the trajectory of the ball must be symmetric about the vertical center line, Thus the ball must enter pocket D as it leaves pocket B.
Log in to reply
Only because the height is odd. If the base were 6 and the height 2 , the ball would end up in C .
Log in to reply
Oh sorry.
I forgot to mention that if both the base and height are even integer then the ball may end up in other pockets too.
Thank you for making it clear.
Log in to reply
@A Former Brilliant Member – Basically, what matters is the evenness and oddness of what you get if you divide the height and width by their highest common factor.
Does this problem belong to the 100 Day summer challege or it is just a sample?
Same method :)
Excellent solution sir, but can you explain the importance of the angle(45) in your solution, what happens in the 60 degree case for instance?
Log in to reply
Is it because we cannot find a common multiple between rational number and a irrational number, so ball will never fall in the pocket?
Log in to reply
Since the ball is always travelling at 4 5 ∘ to the sides, the horizontal and vertical distances it travels are the same. As you say, if the angle were 6 0 ∘ , we would never end up in a pocket.
That's exactly what I did. Beautiful solution.
Well I did this and got it wrong but cant see where I went wrong.
Followed Cartesian co-ordinates and lead me quickly to pocket A. * denotes variable reducing moving X left or Y down
(0,0)
(67,67
)
(100
,33
)
(67
, 0)
(0,67) A !
What did I do wrong?
Log in to reply
From ( 6 7 , 6 7 ) you go 3 3 across and 3 3 down to ( 1 0 0 , 3 4 ) , not ( 1 0 0 , 3 3 ) .
Hi I liked your approach but if it were ant arbitrary angle how would your method work?
Log in to reply
It would tell you that the ball can only be potted if the tangent of the angle α at which the ball is travelling to the horizontal pair of sides is rational. The ball will pot after travelling X table widths and Y table heights, so travelling 1 0 0 X horizontally and 6 7 Y vertically. Thus 1 0 0 X 6 7 Y = tan α must be rational.
That is a very smart way to think about it. I misclicked and got it wrong.
though it took a long, for me to grasp it, but when it happened, i was like OMG, how could someone think like that
In order to find the intersection points,instead of reflect the line, we can "reflect" the rectangles.
Thanks to Rohit Upadhyaya,I found the mistake in my origin solution, the "reflection" times are wrong. Sorry for the confusion caused by the diagram of mine.
Precisely speaking, the "reflection" times in horizontal direction is 67- 1 = 66, and the vertical direction the "reflection" time is 100-1 = 99. When the "reflection" times in horizontal direction is EVEN, so the Line AB still stand at the left side of the rectangle, the "reflection" times in vertical direction is ODD, so the Line BD will at the top side of the rectangle. So the answer is D.
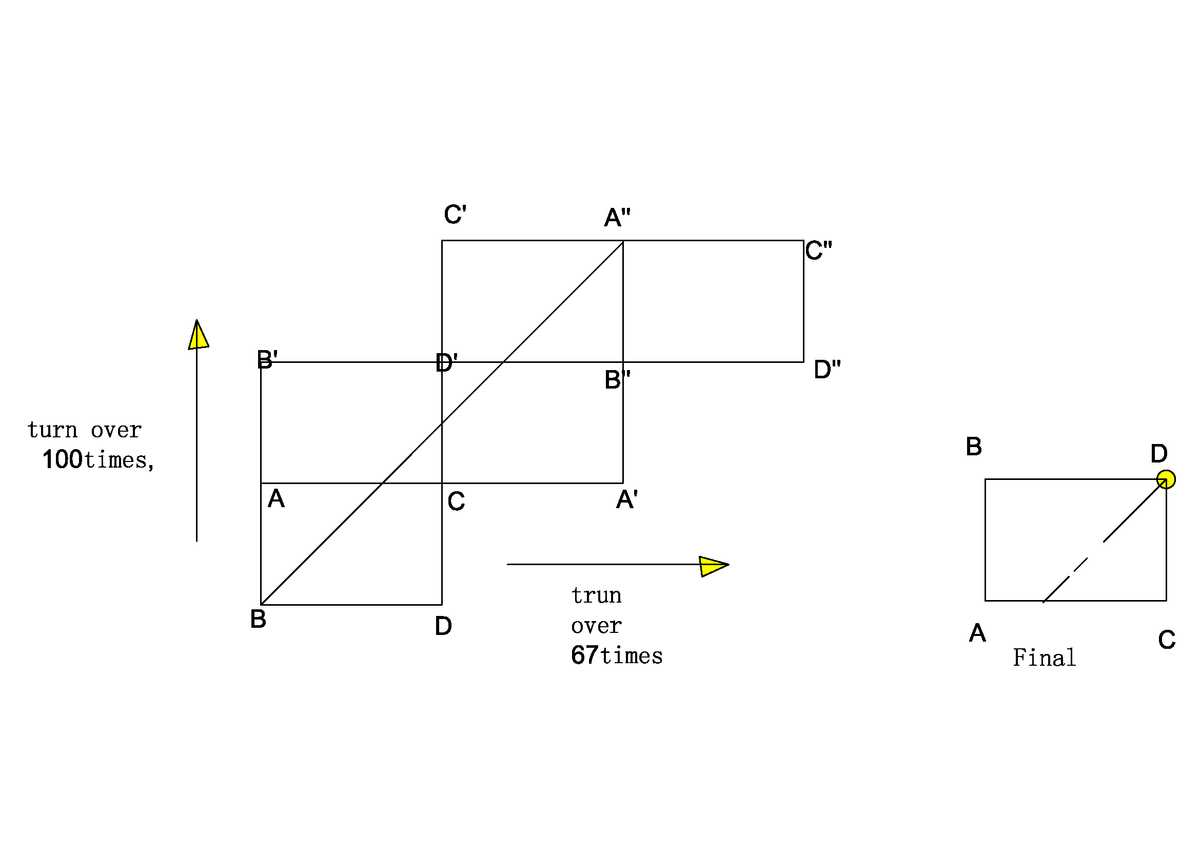
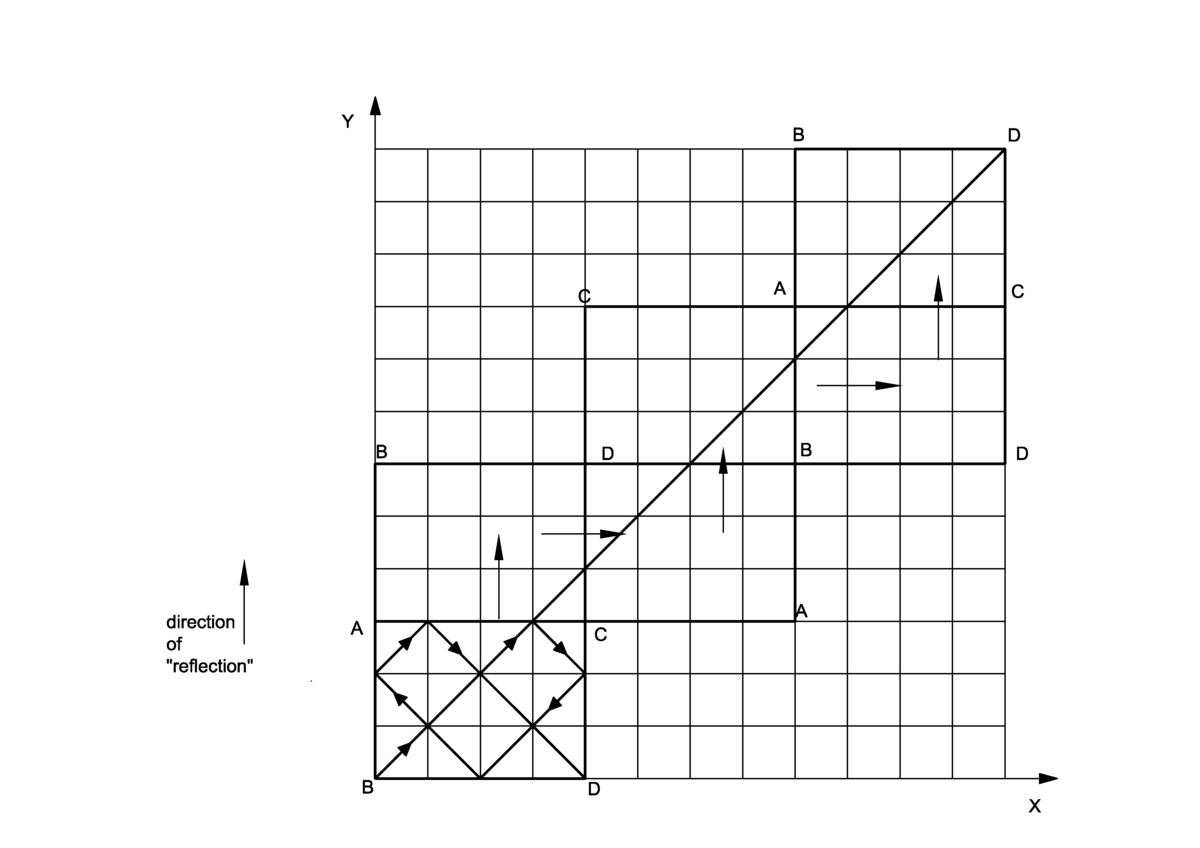
I made a simpler version diagram of the this question, a 4x3 rectangle situation, hope it will help.
Yup, I did it the same way. I think this can be generalized into any angle, but you need to figure out the sequence of reflections that repeats periodically, which depends on both the angle and the ratio of sides' length.
This was my approach, and I think it's the most elegant (although I am biased!).
Just a question, in your final diagram, does the labeling of vertices of the second rectangle correspond to the holes in the pool table in the question ? I'm asking because the question has them labeled differently with A and B, C and D interchanged and the right answer is D in the question which corresponds to C in your diagram.
Log in to reply
First of all, thanks for your question, I review my solution description and I found the mistake, the "reflection" times are wrong. Precisely speaking, the "reflection" times in horizontal direction is 67- 1 = 66, and the vertical direction the "reflection" time is 100-1 = 99. When the "reflection" times in horizontal direction is EVEN, so the Line AB still stand at the left side of the rectangle, the "reflection" times in vertical direction is ODD, so the Line BD will at the top side of the rectangle. So the answer is D. Second, the labels correspond to the holes, and the centers of the holes coincident with the vertices of the rectangle as the question discribed. Thirdly, I made a simpler version diagram of the this question, a 4x3 rectangle situation. I appended it to my solution, hope it will help a little. Thanks again.
In your top diagram it appears to hit A perfectly. Why is A not the answer?
Log in to reply
Probably because 6 7 / 1 0 0 is almost equal to 2 / 3 . The line y = x passes close to the point ( 2 0 0 , 2 0 1 ) , but doesn't actually go through it.
If you draw the path on a grid as you did for your 3x4 rectangle example, it brings up a couple interesting points. First, if the side lengths AB, BD of the rectangle are relatively prime, it appears obvious from doing a few simple examples that the ball's path will traverse each square in the grid exactly once. If this is true, it is easy to see that the ball will land in pocket D if the side BD has an even integer length and side AB an odd integer length. The ball will land in pocket A if side AB has an even integer length, and side BD has an odd integer length. It will land in pocket C if both sides AB and BD have odd integer lengths.
Zheng Yue: According to you, the ball has traversed 3 horizontal units = 3 100= 300 units and 4 vertical units =4 67= 268 units. But since the ball is traversing in 45 Degree angle it will cover horizontally and vertically same distance, from your diagram it is not covering the same distance...
What a nice way to put it into a diagram. It reminded me a book wrote by Dr. Carlos Boch, back here in México "El billar no es de vagos" which could be translated as "Billiards is not for loiterers". There he explains how you can use the same line of reasoning you used to find the gcf of two numbers.
thanks for hlp
Hopefully this is right. Here it goes:
The 45 degree angle is very convenient, since it partitions the speed equally between the vertical and the horizontal. We therefore know that at any given time, the total distance traveled in the horizontal direction equals the total distance traveled in the vertical direction. Suppose that the ball will land inside a pocket. This means that the travel distance in either dimension must simultaneously be an integer multiple of 67 and an integer multiple of 100. The smallest number which satisfies this condition is 6700, which is the LCM of 67 and 100.
6700 = 67 x 100, which is an odd multiple of 100
6700 = 100 x 67, which is an even multiple of 67
Now we need to associate the sides with either even or odd multiples. The top side (AC) corresponds to odd multiples of 67, and the bottom side (BD) corresponds to even multiples of 67. The left side (BA) corresponds to even multiples of 100, and the right side (DC) corresponds to odd multiples of 100.
Since we have an odd multiple of 100, and an even multiple of 67, the pocket must be on the right side (DC) and the bottom side (BD).
We therefore have Pocket D as the answer.
Find the solution experimentally. Draw simple rectangles of differing dimensions, say 3x2, 3x3, 3x4, 4x2, 4x3, 4x4, 4x5, etc. Draw the paths of the ball. You will find that when the ball hits the x-axis (y = 0) or the y-axis (x = 0), the value of x or the value of y is always an even integer, a multiple of 2. So if the x dimension is even and the y dimension is odd, as in this problem, the ball will end up in the lower right. If the x dimension is odd and the y dimension is even, the ball will end up in the upper right. if both x and y are odd, the upper right corner is the only possibility. If the original dimensions are both even, reduce the dimensions until you have odd-even, even-odd, or odd-odd, and you will have the easy solution.
I absolutely think that your answer is wrong and that it should be A without a doubt. Let me explain to you my theory:
- The situation utilizes the law of reflexion, which stipulates that the incident angle is equal to the reflexion angle. In this situation, by applying this theorem, we can assume that isocele triangles are formed from this step. In this direction, the respective measure of these triangles is equal in these situations, which leads to a diagram where the rays' trajectory finishes in the pocket A.
Log in to reply
You are right that "the incident angle is equal to the reflection angle". That is a crucial aspect of the proof, which is where Steven concludes that "horizontal distance traveled equals vertical distance traveled".
Can you elaborate on how the rest of your solution goes, and how you conclude that "which leads to a diagram where the rays' trajectory finishes in the pocket A."?
Imagine the pool table as a Cartesian grid, with pocket B as the origin. Since the ball leaves (0,0) at a 45 degree angle, it is traveling along a line with slope 1. If we know (from physics) that the ball will bounce off any wall in such a way that the angle its path makes with that wall will be preserved, then we can say that the ball will also leave any wall it bounces off of at at 45 degree angle. This implies that the ball can either be traveling along a line with slope 1 or slope -1. In the first case, it is gaining or losing horizontal and vertical distance equally; in the second, horizontal distance and vertical distance are being converted into one another.
This gives us four types of motion the ball can be making at any time. After some increment of time along a given path, the ball's position will have changed by some multiple of either (1,1) or (-1,-1), if on a line of slope 1, and (1,-1) or (-1,1) if on a line of slope -1.
But this means that for integer coordinate pairs, the parity of the sum of the coordinates remains constant. In other words, adding a multiple of (1,1), (-1,-1), (1,-1), or (-1,1) to a point will give you a point with coordinates whose sum will be even if the starting point's sum was even, and odd if the starting point's sum was odd.
Since we start at (0,0), which has an even sum, the odd sum points (0,67) and (100,67) are unreachable. This rules out pockets A and C.
We also know that since the only path out of (0,0) that is on the table (under these rules), is in the direction (1,1), the only way into (0,0) would be the opposite direction (-1,-1). This means that the ball would have to reverse its path somewhere, which from angle preserving property of collisions we know would only be possible if it precisely hit another corner. Since that would end the path, we rule out pocket B.
Therefore, if the ball goes into a pocket it has to go into pocket D.
But before we can say it definitely goes into pocket D, we have to consider the possibility that "The ball will never land in a pocket."
But if it never lands in a pocket, it travels for an infinite distance on the table. We can rule out the possibility of the ball getting into an infinite loop by noticing that if at any point we reversed the balls motion (such as by placing a wall in its path perpendicular to its motion), it would trace out the exact same path on the table, except in to opposite direction. So it can't get into a loop because there's no way to reverse a loop that gets the ball to end up back at point (0,0). A loop like that would have to have two different histories of where the ball had been, which doesn't make sense here.
We also can rule out any way for the ball to travel an infinite distance without looping, because if we consider the ball as effectively moving alongs integer coordinate pairs to integer coordinate pairs along a path (1,1), (-1,-1), (1,-1), or (-1,1), then there are a finite number of states the ball-table system can actually be in (something like 68*101 points times 4 directions divided by 2 for the parity constraint = 13,736 distinct states as an upper bound). So the ball can't travel an infinite distance without the whole system repeating itself at some point. This seems to rule out the possibility that "The ball will never land in a pocket."
Therefore the ball lands in pocket D.
Imagine the table is on a grid, where pocket 'B' is at point (0,0), 'A' at (0,67), 'C' at (100,67), and 'D' at (100,0). Define even (odd) points as points where the sum of coordinates is even (odd). Among pockets 'B' and 'D' are even; 'A' and 'C' are odd. Since the ball moves at a 45 degree angle, every side point (i.e. not a pocket) is connected to exactly two other points (regardless of direction); pockets are connected to only one other point. Also, note that 'even' points only connect to 'even' points, and 'odd' to 'odd' (again b/c of 45 degree angle). Therefore, a path starting at 'B' (even) cannot end up in 'A' or 'C' (odd). Also, since no point reflects back, once a point has been hit, it can't be hit again, unless it's in a loop. The possibility for loops, however, can be ignored b/c a loop cannot contain a pocket. This means the path can't go reverse, and so a ball starting at 'B' can never come back to 'B'. Since there are a finite number of points, the path must end somewhere, and the only place it can end (by elimination) is 'D'.
I mean points are connected by the path the ball traces out.
Can you explain what you mean by: "Since the ball moves at a 45 degree angle, every side point (i.e. not a pocket) is connected to exactly two other points (regardless of direction); pockets are connected to only one other point." I don't understand how they are "connected"
Using a ruler, the ball will hit around the 3rd dot from the bottom right corner, then it will move 90 degrees to a line parallel to the 2nd line, then it will hit around the 1st dot down from the top left corner, then to the 1st dot to the right of that corner, which will aim it straight at Pocket D. Another way to figure it out is that every time it hits a wall, it will form triangles that get smaller to the point where it will go into Pocket D.
Pretty new to this website, (and math puzzles) so forgive me if my answer is all over the place. My method got me the correct solution, but I'm not sure if my reasoning was legitimate, or I was just lucky. Here we go: After a minimum of three bounces off of the walls of the table, a polygon can be formed by connecting each point where the ball hits the wall. In other words, after three bounces, connect the points where the ball hits the wall between pockets AC, CD, and BD to form a triangle. After four bounces, a four-sided polygon can be formed, this time using an additional point between AB, etc.
For every bounce, the sum of the internal angles of that polygon is 180(B-2), where B>/ 3, and equals the number of bounces (not including the 45 degree initial angle). When the ball lands in a pocket, another 45 degree angle is formed between the ball and the pocket, and we have a closed figure. As each individual angle formed at a bounce is 90 degrees (assuming equal angles before and after the bounce), then the sum of the interior angles of the polygon will be 45+90B+45, where the two 45 degree angles are from the initial and final pockets.
Finally, to make a long story short, set 180(B-2)=90B+90, B=5 bounces before landing in a pocket. Starting at pocket B, the ball goes to AC (bounce one), CD (bounce two), BD (bounce three), AB (bounce four), AC (bounce five), and, lands in pocket D. Let me know what you guys think!
Let (x, y) denote the ball's current position on the coordinate plane. Note that the x direction and y direction are both increasing at either the exact same rate or their inverse—that is, y=±x because it is a 45 degree angle. Also notice that for a ball to land in any hole, ball must have either 0 or 100 units as the x-coordinate, equivalent to 0 (mod 100). Similarly, the y-coordinate of the ball must be either 0 or 67, both of which are 0 (mod 67). Thus, x must be 0 (mod 100) and y must be 0 (mod 67). lcm(67,100) = 6700, so the ball goes back and forth horizontally 6700/100 = 67 times, or an odd number, and vertically 6700/67 = 100 times, or an even number. Thus, the vertical movement cancels out, but the horizontal movement is equivalent to crossing the board exactly once, meaning the answer is D.
I just used cad and drew the lines. Took about 3 minutes.

The Numbers of bounces seems to be 67+100-2 = 165. If you have table size m times n, I think the number of bounces is always n+m-2 if the numbers are relative Co-prime. I am trying to prove this but I have not yet been successful here. Is there anyone out there who can prove it?
Just for variety, I wrote a simple simulator in Excel. First few rows of the worksheet are as follows: link text and then you just copy the bottom row down far enough. I'm aware this is a programmatic solution rather than a mathematical one - just though someone might be interested.
I realized that to go in a pocket the ball must come off a long cushion 67 from a "far" end. I traced the ball around a couple of times and realized that it was bouncing of the top long side at (99-2n) from pocket C. It will therefore go in pocket D.
A corollary of the elegant LCM and traversal parity methods is that the ball can never go in pocket B! This is a bit of a surprising result to me but the logic is correct. If the table measures X length and Y width and both measures are even then in some other integral unit of measurement the table will have at least one of X or Y to be odd and so the answer must be A, C or D, never B.
At every reflection the ball would get a 90 angular projection and thus u can easily trace the ball by summing up the angles made by it as the total angle of quadrilateral.
Let’s put our table on a grid. It is 100 in the X direction and 67 in the Y the angle of 45º This which mean the increase in X to Y is 1:1 we then get out first bounce at 0,0 to 67,67 this then bounces down to 100,34 this bounces down and left to 66,0 which again bounces up to 0,66 which quickly goes infront of A to 1,67 which then bounces to 68,0 to 100,32 to 65,67 to 0,2 to 2,0 to 69,67 to 100,36 to 64,0 to 0,64 to 3,67 to 70,0 to 100,30 to 63,67 to 0,4 and on until it will reach 100,0 eg D
at 45 angle it means the ball will cover maximum distance so it will go to D
Due to the initial +x trajectory of the ball, it cannot enter pockets B or C. If it makes a full vertical traverse an even number of times and enters a pocket, it will be D. If it makes a full vertical traverse an odd number of times and enters a pocket, it will be A. To enter a pocket it must travel a common multiple of 67 and 100, the first of which is 6700, which involves an even number of vertical traverses, so pocket D.
first i thought that the ball will end up in the point of A, but think a little more...it cannot exactly go straight away into this point, so it will end up in the D.
Use the plane as a covering space for the rectangle in the following manner: ( x , y ) → ( x ′ , y ′ ) where x ′ = ( x m o d 2 0 0 ) if ( x m o d 2 0 0 ) < 1 0 0 , otherwise x ′ = 2 0 0 − ( x m o d 2 0 0 ) Similarly let y ′ = ( y m o d 1 3 4 ) if ( y m o d 1 3 4 ) < 6 7 , otherwise y ′ = 1 3 4 − ( y m o d 1 3 4 ) .
Then the line y = x is an exact cover for the path of the billiard ball. The billiard ball is going right when ( x m o d 2 0 0 ) < 1 0 0 and left when 1 0 0 < ( x m o d 2 0 0 ) < 2 0 0 . Similarly it is going up (according to the picture) when ( y m o d 1 3 4 ) < 6 7 and down when 6 7 < ( y m o d 1 3 4 ) < 1 3 4 . It reaches a pocket when x ′ = y ′ = 0 . The first time this happens is (since 6 7 and 1 0 0 are relatively prime) at the point ( 6 7 0 0 , 6 7 0 0 ) .
To determine the pocket, consider what direction the ball is traveling at ( 6 6 9 9 , 6 6 9 9 ) . Now 6 6 9 9 = ( 9 9 m o d 2 0 0 ) , so the ball is going to the right here. And 6 6 9 9 = ( 1 3 3 m o d 1 3 4 ) , so the ball is going down here. Thus the pocket the ball ends up is in the lower right corner, pocket D .
To end in a pocket, the ball must travel an integer number of table widths and an integer number of table heights at the same time . Since 6 7 and 1 0 0 are coprime, the first time this happens is when the ball has travelled 6 7 table widths and 1 0 0 table heights.
At this point, the ball will have crossed the table horizontally an odd number of times, and so will be at the right-hand edge. It will also have crossed the table vertically an even number of times, and so will be at the bottom edge. Thus it will be in the bottom-right corner, and go into pocket D .