Can you tell the difference?
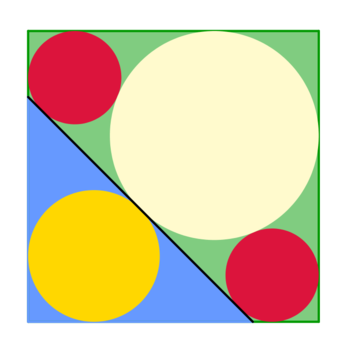 In the figure, four circles are inscribed in a square. The circles are tangent to each other as well as to the sides of the square and to the black line segment. The two red circles are identical.
Compare the
b
l
u
e
area with the
g
r
e
e
n
area.
In the figure, four circles are inscribed in a square. The circles are tangent to each other as well as to the sides of the square and to the black line segment. The two red circles are identical.
Compare the
b
l
u
e
area with the
g
r
e
e
n
area.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Can you help me understand the geometry behind:
r 3 + ( r 1 + r 3 ) 2 − ( r 1 − r 3 ) 2 + r 1 = 1
Log in to reply
Log in to reply
Thanks. I hated to draw the figure.
Log in to reply
@Chew-Seong Cheong – Thank you for posting your solution. Happy new year!
Thank you both.
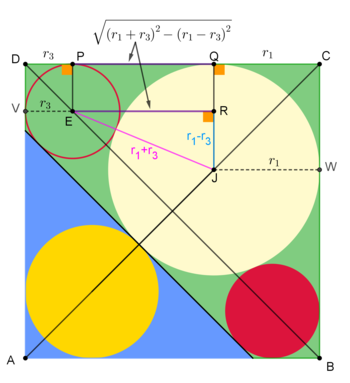
Let the side length of the square be 1 , the radii of the white, yellow and red circles be r 1 , r 2 , and r 3 respectively.
We note the side length of the square is given by:
r 3 + ( r 1 + r 3 ) 2 − ( r 1 − r 3 ) 2 + r 1 r 3 + 2 r 3 r 1 + r 1 ( r 3 + r 1 ) 2 ⟹ r 3 + r 1 = 1 = 1 = 1 = 1 . . . ( 1 )
The diagonal of the square is given by:
( 2 + 1 ) ( r 2 + r 1 ) ⟹ r 2 = 2 = 2 − 2 − r 1 . . . ( 2 )
The length of the black line segment is given by both ℓ = 2 r 3 cot 2 1 3 5 ∘ + 4 r 3 r 1 and ℓ = 2 r 2 cot 2 4 5 ∘ . Therefore, we have:
r 3 cot 2 1 3 5 ∘ + 2 r 3 r 1 ( 2 − 1 ) r 3 + 1 − r 3 − r 1 ( 2 − 2 ) r 3 + 1 − r 1 + ( 2 + 1 ) r 1 ( 2 − 2 ) r 3 + 1 + 2 r 1 ( 2 − 2 ) ( 1 − r 1 ) 2 + 1 + 2 r 1 ( 2 − 2 ) ( 1 − 2 r 1 + r 1 ) + 1 + 2 r 1 2 ( 2 − 1 ) r 1 + 2 ( 2 − 2 ) r 1 − 1 ⟹ 2 r 1 + 2 2 r 1 − 2 − 1 ⟹ r 1 = 2 3 + 2 1 − 2 + 2 r 2 = 2 1 − 2 3 + 2 + 2 r 3 = 2 5 + 2 1 − 2 + 2 − 2 ( 3 + 2 − 2 2 + 2 ) = r 2 cot 2 4 5 ∘ = ( 2 + 1 ) r 2 = ( 2 + 1 ) ( r 2 + r 1 ) = 2 = 2 = 2 = 0 = 0 ≈ 0 . 3 5 9 3 4 7 7 1 6 1 6 4 ≈ 0 . 2 2 6 4 3 8 7 2 1 4 6 3 ≈ 0 . 1 6 0 4 3 5 3 4 8 7 8 4 Note that r 3 + 2 r 3 r 1 + r 1 = 1 and ( 2 + 1 ) ( r 2 + r 1 ) = 2 and r 3 + r 1 = 1 From (2) From (1)
Note that the area of the blue triangle is Δ b l u e = ( 2 + 1 ) 2 r 2 2 and then the blue area A b l u e = Δ b l u e − π r 2 2 ≈ 0 . 1 3 7 7 6 6 0 7 9 5 2 3 and the green area A g r e e n = 1 − Δ b l u e − π ( r 1 2 + 2 r 3 2 ) ≈ 0 . 1 3 3 7 4 7 9 7 6 3 2 7 . Therefore
A b l u e > A g r e e n