Cannon on a Cliff
When a cannon is on the ground, the cannonball lands the farthest from the cannon if it's shot at a 4 5 ∘ angle.
Now, when the cannon is on a cliff, what shooting angle θ makes the cannonball land the farthest?
Details and Assumptions:
- Neglect air resistance.
- The cannon shoots the cannonball at the same speed regardless of the angle of projection.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
hate to be the jerk but technically there's no lift or thrust going on here. Still a good explanation though!
Log in to reply
I suppose I didn't mean lift or thrust in the proper physics sense. I was trying to give an intuitive feel to the situation.
I understand the explanation, but could that not be said when there is a ditch or if the original ground is the cliff? Then would 45 degrees not be the optimal angle? Because are we not basically transitioning the ground to the height of the cliff?
Log in to reply
I'm not sure of your question. The higher the cliff, the lower the angle. θ would be a continuously decreasing function of height.
I understand the explanation, but it doesn't seem especially rigorous. My own (equally unrigorous) approach was to observe that when the cannonball has returned to the same height as the cannon it is travelling at the same angle it was launched. The extra horizontal distance that it travels from that point to the ground is maximised by having the cannonball pass this point as near horizontal as possible. This would suggest that it is better to lower the initial angle from 45 degrees. But how do I know the extra distance achieved in stage 2 (from cannon-height to ground) is greater than the distance lost in stage one (from cannon to cannon-height)? Given that there are no precise measurements involved I simply imagined a very weak cannon and a large vertical drop. Regardless of angle the cannonball would not travel very far from start back to 'cannon-height' but thereafter if the drop was large enough it could travel forward a long way by entering the drop almost horizontally.
What about mathematical expression concerning the range of the projectile, that is, d = (v^2 / 2g)(1+ sqrt(1+(2gy)/(v^2sin^2(angle)))sin(2angle) ? From this derives, either the cannon is on the ground or on some cliff, that maximum horizontal distance, i.e. d, is when the angle of shooting the ball equals 45 degrees.
Oleg Yovanovich
April 14, 2019
Projectile motion is parabolic with a decreasing slope.
When the cannon and ground are at equal heights, the optimal angle of launch is 45 degrees but it is better to think that the reason for this is that the angle of impact is 45 degrees. This is the angle after which the motion is predominantly vertical, wasting effort if the goal is to maximise horizontal distance.
If the angle of impact has to be 45 degrees, the motion is parabolic and the cannon is above ground, the angle at interception of the parabola and cannon is less than 45 degrees.
This reasoning also tells you need steeper angle of launch if the cannon is below ground level.
the question didn't tell me how much higher than the 45 degree cannon the unspecified cannon was. More height = less necessary angle is a weird one. It's useful to think about gravity and the amount of kinetic energy released as a launching mechanism at the launch. I got the answer wrong because I only had 1.5 pieces of information and my dumb brain couldn't evaluate the 2 cannon launch positions on the basis of the 1.5 infobits.
Log in to reply
Hi LD, you are right. The cliff elevation(h) should have been stated to be at least Vi^2/4g, where Vi=initial velocity and g~10m/sec^2. For lower elevation, the range(R) will be lower even if the firing angle(x) is 0 <= x < 45. Rground_cannon=2Vi cos(45) root(2h/g)=Vi^2/g > Vi cos(x) (root(2y/g)+2Vi sin(x)/g)for y < h. Let x=30°, Vi=100m/sec, h=250m, y=200m 0.866Vi (root(2y/g)+2Vi/g) < Vi^2/g? 0.866 100 (root(2*200/10+200/10) < 100^2/10; 86.6(40+20) < 1000m; 670.82m < 1000m
Log in to reply
Typo, 0.866100(root(2 200/10+200/10) should've 0.866 100(root(2*200/10)+200/10))=670.82m
Log in to reply
@Jun Bangues – Typo again, 0.866100 should've 0.866*100
Log in to reply
@Jun Bangues
–
That's not a typo, it's because the comment processing turns
*
into a formatting command. Try using LaTeX to write
1
∗
2
∗
3
instead of 1
2
3... ;-)
By the way, did you know you can edit your comments? B-)
If you have to estimate 30 degrees then that's problematic too, albeit the elevated cannon 'looks' 1/3 less angled skyward. Were we meant to use our eyes or hold a ruler up to our laptop screens? Did I have to look up a nice short expression of g? All that being said you can do all sorts of geometric calculations to generate intersecting semicircles or generate a 3rd angle using the base of the elevation as another angle etc. Anyway 0.866100 is broadly .87 which = -1.13 which is an expression of 1/3 (NOT one third, but digits rather than values), which is what we visually suspected was the difference between 45 degrees and the angle of the elevated cannon. Therefore to calculate the difference of any 2 cannons in a similar example we can say it will be -1.(ground cannon angle - elevated cannon angle). This isn't good maths, but it would work assuming you could use manual tools to measure the angles in a given example, or any nice example where the angles are different by some value you can intuit by cardinality.
What about the argument that shooting at a 45 degree angle maximizes the distance that the ball travels before falling back to the same level. Then if this distance traveled for falling back to same level is maximized, there is even additional horizontal distance traveled as it falls to ground.???
Log in to reply
That's where the height of the cliff comes in. For higher cliffs, it is easier to see that the "additional horizontal distance traveled as [the ball] falls to ground" can be overcome by a lower angle... Something like this:
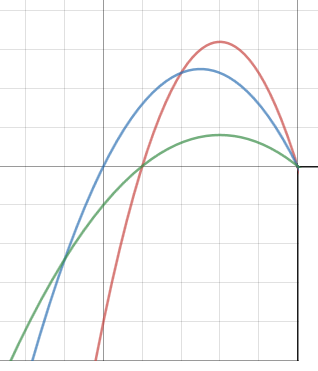 (disclaimer: those are not actual trajectories, just random parabolas to help visualize what's going on)
(disclaimer: those are not actual trajectories, just random parabolas to help visualize what's going on)
But the angle of impact of the ball from the elevated cannon in the maximal-range case is NOT 45°, it's > 45°. If the elevated cannon shoots at 45°, the ball will pass back through the plane of the cannon (parallel to the ground in this approximation) directly above the point where the ball from the ground cannon strikes the ground and at an angle of 45°. But it will still have forward velocity, so it will travel further. And as you point out, the trajectory of the falling ball becomes continuously steeper, and after the maximal range is reached (impact angle 45°), it is steeper than 45°.
(Not that this affects the reasoning, but the trajectory of the cannonball is elliptical, not parabolic. It is in orbit around the Earth's center of mass, though the orbit intersects the Earth's surface. As we've known since Kepler deduced and Newton explained, closed orbits in a centrally directed inverse-square force field (i.e., real-world gravity) are ellipses, with circular motion a limiting case. "Parabolic" is a Physics for Poets approximation that is "close enough" only over short distances. The problem as ordinarily presented implicitly assumes both that the force of gravity does not depend on the cannonball's height above ground/distance from Earth's center of mass (i.e., is constant rather than inverse-square) AND that the gravitational vectors along the trajectory are parallel (i.e., are not centrally directed, toward Earth's center of mass).)
Log in to reply
Although, Howard, while Chris is wrong that the impact angle should be 45° for maximum range, your argument isn't quite valid either. The maximum range is NOT when launch angle is 45°, which would indeed make the impact angle higher than the launch, qed as you mention above, but in the current problem of "cannon on a cliff", the launch angle is LESS than 45° and the impact will be higher than that, but you don't know exactly how much. Maybe sometimes it can even be exactly 45°.
Now, i wish i could provide specific values, but my calculus is a bit rusty. I'll try to adapt to the solutions given by Denis and Kelvin.
Let's assume initial speed is 10 m/s and height of cliff is successively 0m, 10m, 20m, 50m, and 100m. (For imperial units the results should be the same, just read every "m" as "ft")
For 0m, we get the usual cannon problem, angle = 45°, horizontal velocity = vertical velocity = 7.071 m/s, time of "flight" = 1.442s, range = 10.197 m.
For 10m, according to Denis' solution below, angle is α = 2 1 × a r c c o s ( g h + v 2 g h ) =30°9'40.317''. For the time of flight, i'll use Kelvin's solution so t = g × s i n ( α ) v =2.02955s, then range = 17.5478m.
Using an angle of 45° would give a time of 2.32s and a range of 16.41m.
Using an angle of 0° would give a time of 1.428s and a range of 14.28m.
For h=20m, angle is 24°15'42.15'', time = 2.4816s, range = 22.6245m
For h=50m, angle is 16°55'10.511'', time = 3.5s, range = 33.5216m
And finally, for h=100m, angle is 12°25'16.919'', time = 4.74s, range = 46.297m
Imagine a cannon at ground level that shoots a cannonball such that it passes through the location of the cliff-cannon at the required speed. This cannon is angled at 45''. When the cannonball passes through the location of the cliff-cannon, its angle of trajectory is <45''.
Initially, I liked the intuitive simplicity of this solution. However, strictly speaking, this maximizes the horizontal distance from where the cannonball passes through ground level on the way up to where it hits the ground. I’m not sure it’s immediately obvious that also maximizes the horizontal distance from the launch point.
Log in to reply
There are many parabolas that start and end at 45° to the ground.
To use this step requires that, given a certain height and velocity, only one of such parabola mentioned above exist. Which I believe is possible to make intuitive but im too lazy to think right now.
Something is wrong here. If the motion is perfectly parabolic, and the initial angle of the trajectory is 45 degrees up, then the angle of the trajectory, when the shell comes down, is 45 degrees down when the shell reaches the initial height from which it was fired. This means that the shell has forward motion during its final fall from cliff-height to lower level. Everyone is wrong: I am right.
Yes, the distances are measured starting from different points and also the speed of the imaginary cannonball shot from ground level is not the same as the initial speed when it passes through the real cannon... the thinking is interesting but it is not rigorously accurate.
I have used some calculus (not much) and reached the result that the initial height h, the maximal distance x and the shooting angle theta are related by x/h= tg(2 theta). Therefore, for h =0 one has theta = 45, but for h > 0, tg(2 theta) must be finite and positive, hence theta < 45.
Assume the initial velocity is u , shot angle be θ , initial height from the ground is h > 0 , the time taken to hit the ground is t , then we have − h = u t sin θ − 2 1 g t 2 And then the range can be expressed as R = u t cos θ
Take derivative with respect to θ to the first equation, yields 0 ∴ d θ d t = u ( sin θ ) d θ d t + u t cos θ − g t d θ d t = g t − u sin θ u t cos θ
To find the extreme point on range, we should have: d θ d R u ( cos θ ) d θ d t − u t sin θ ∴ d θ d t = 0 = 0 = t tan θ
Link the two expressions of d t / d θ we have g t − u sin θ u t cos θ u cos 2 θ u sin θ = cos θ t sin θ = g t sin θ − u sin 2 θ = g t sin θ = g t u
But if we solve for t in the expression of h : g t 2 − 2 u t sin θ − 2 h = 0 , we will have one positive value and one negative value. Take positive as appropriate solution: t = g u sin θ + u 2 sin 2 θ + 2 g h > g 2 u sin θ
Then we have sin θ = g t u < 2 sin θ 1 which leads to sin 2 θ < 2 1 ⟺ sin θ < 2 1 .
This says that θ must less than 4 5 ∘ .
Ps: I like to solve Physics problem mathematically...
I stumbled over this problem when a physics book I read mentions about the optimun angle of projection for javelin throwers. I derived the formula for the distance but I could not find the maximum, so I have Geogebra do the work. However, I don’t know how to load an image from my decice, so please show me here so I can load it.
Anyway, can you explain why s i n ( θ ) = g t u ?
I also like to solve physics problem mathematically, but sometimes using physical reasoning is just as great.
Log in to reply
I just use 'Snipping Tool' on every computer, easy way. As you can see I have derived two equations about d θ d t , the result you noticed is what we can get after equal them. I don't like physical reasoning to be honest, because sometimes we may just too careless to notice every necessary thing.
Sorry for asking that question, but what does that sign with the three little points in a triangle stand for?
Log in to reply
It is a symbol used for the word "Therefore" and the symbol used for the word "Because" is ∵
Log in to reply
OK, M first 'PC' was a Mac and there was a keyboard shortcut for the 'therefore' symbol. It appears to be lacking in Windows PC's ... Correct me if I'm wrong.
Nice write up and solution Kelvin Hong!
I went through a similar procedure. I just wanted to add that you can use comparative limits making using very small and large h values when solving for t and plugging the corresponding t into your R equation.
These nicely and correctly result in the maximum angles being θ ≈ 0 ∘ for h > > u sin θ , ie. a very large hill and θ ≈ 4 5 ∘ for h < < u sin θ , ie. a very small hill or nearly flat ground.
Limits usually make for good insanity checks to make sure the equations are working the way you want them to and can reduce some of the math while still giving insight into the system.
I have a more mathematically worked out solution for anybody interested. Let h 0 be the initial height, v 0 be the initial velocity, θ is the angle between horizontal and cannon, g be gravity and t be time, then the following equations of motion hold:
x y = v 0 cos θ t = h 0 + v 0 sin θ t − 2 1 g t 2
Solving for t in second equation and plugging into the first gives:
0 = h 0 + x tan θ − 2 v 0 2 g x 2 sec 2 θ
Since x = x ( θ ) is a function of the angle, we can implicitly differentiate the above in terms of θ :
0 = x ′ ( θ ) tan θ + x sec 2 θ − 2 v 0 2 g [ 2 x x ′ ( θ ) sec 2 θ + 2 x 2 sec 2 θ tan θ ]
We want the maximum angle so set x ′ ( θ ) = 0 . Then the equation contains the max angle α and the max range d :
0 0 = d sec 2 α − v 0 2 g d 2 sec 2 α tan α = d sec 2 α [ 1 − v 0 2 g d tan α ]
We don't want d = 0 and clearly sec 2 α = 0 therefore:
0 d tan α = 1 − v 0 2 g d tan α = g v 0 2
Now we can plug the above into the equation we derived above which relates x and θ , rearranging a bit and manipulating it will yield:
0 = h 0 + g v 0 2 − 2 g v 0 2 csc 2 α
Which we can rewrite as follows:
sin 2 α = 2 ( g h 0 + v 0 2 ) v 0 2
Using a trig identity we can finally write it as follows:
cos ( 2 α ) = g h 0 + v 0 2 g h 0
From there we can solve for α and so on... Here we can see that the maximum angle α depends on the initial height h 0 and the initial velocity v 0 so there is no definite answer for the maximum angle like the simple case. However we DO know that the angle is between 0 and 45 because
g h 0 + v 0 2 g h 0 > 0
When this term IS zero, that is when the cannon is on the ground h 0 = 0 , we get the simple case:
cos ( 2 α ) = 0
Where we can clearly see that α = 4 5 o
But the answer is 0 ∘ < θ < 4 5 ∘ isn't it?
Log in to reply
Correct, that's why g h 0 + v 0 2 g h 0 > 0 that always gives an angle between 0 and 45.
Log in to reply
Oh, you say that when h = 0 , I'm sorry. Nice solution !
See the problem Maximizing Range 2 for mathematical solution.
When on the ground the canon is projected at an angle so that trajectory have both max height as well as distance and the angle in the case is 45° as it is in the projectile motion case. But at a height ,h if we say,the projected angle should be lower as the condition of achieving the max height is compensated by some factor by the height. And As speed is same for both canon balls,So in accordance with upper points the angle should be less than 45 in order to attain the same max distance and the same could be reversed if it was in depression like a hole.
Let H be the point we’re the cannon is located, and P is the point were the cannon reaches its maximum range. Then the cannon must be pointing 45 degrees from the line HP. If H is above ground then the angle theta must be lower than 45 degrees.
Gravity will act longer on the cannonball when shot from the cliff, so you should increase the cosine component of the force which is done by decreasing the angle.
Horizontally S = sinθ * V0 (initial speed) * t Assume the cannon is placed at a extremely high land, and 0<θ<90, t will be extremely large in this case. S will be max when θ is exetremely close to 0.
Logically, if there was no ground level, or the cliff was infinitely high, but you still wanted to launch as far as possible, it would be a waste to have any vertical initial velocity. So if the cliff was infinitely high, the optimal angle would be 0. As the height decreases, the angle increases, probably in some way relating to the tan function. Obviously this isn't rigorous, but it works for multiple choice.
As the canon is above the ground at a height, it has got some 'free altitude' to travel with the help of gravity and gain more horizontal distance than the one on the ground. The angle of launch splits the force imparted on the cannonball into horizontal and vertical components; at a 45-degree angle, the force splits equally and allows it to reach an optimal distance which is a trade-off between and horizontal reach and vertical climb.
Here, as the canon on the elevation gets an extra free altitude to travel, gravity takes care of it as it is coming down; So, to reach farther, more force has to be dedicated to the horizontal component; thus reducing the angle with respect to the 'free altitude' available.
45 degrees is optimum on flat ground because it gives the right balance of lift and forward thrust. If you start higher up, you get some lift for free so can devote more of your charge to forward thrust and can aim lower than 45 degrees.
(If you start in a hole you need more lift and a higher angle.)