Can't even use the perfect square identity!
1 + 2 x + 2 2 x + 1 = y 2
For integers ( x , y ) , how many different solutions are there which satisfy the above?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You may be interested in this problem: A generalization of problem 4, IMO 2006 .
Can you explain why one of (y+1) and (y-1) will be divisible by 4 not 2 ?
Log in to reply
Because every 2nd multiple of 2 is a multiple of 4. Since y − 1 and y + 1 are consecutive multiples of two, it follows one of them is divisible by 4.
Log in to reply
Why one of these factors will be divisible by 2 x − 1 not 2 x .It can be 2 x − r and 2 r
Log in to reply
@Kushal Bose – One of y − 1 and y + 1 will be divisible by 4 , and this means that the other one will be congruent to 2 modulo 4 . Thus the index of 2 in one of them must be 1 , so the index of 2 in the other must be x − 1 .
Log in to reply
@Mark Hennings – @Mark Hennings , please clear my doubt also:
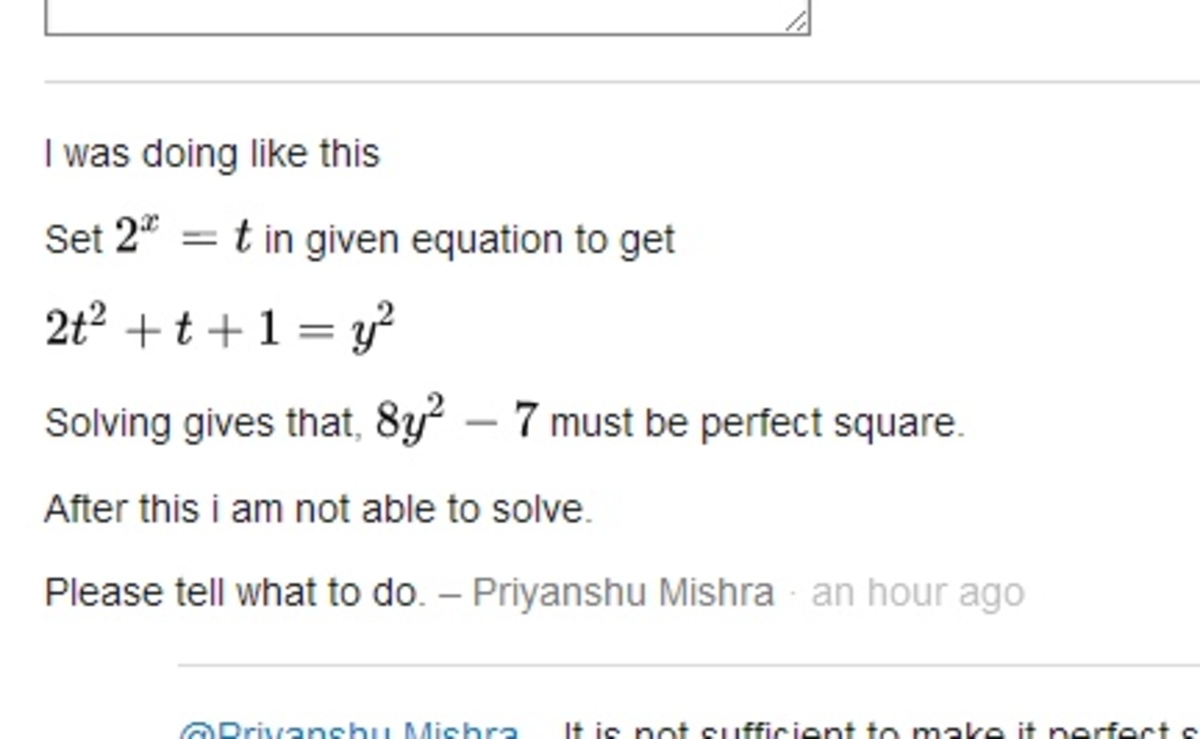
I was doing like this
Set 2 x = t in given equation to get
2 t 2 + t + 1 = y 2
Solving gives that, 8 y 2 − 7 must be perfect square.
After this i am not able to solve.
Please tell what to do.
Log in to reply
It is not sufficient to make it perfect square the whole root should be power of 2
Log in to reply
Yes basically what i am saying is that
t = 4 − 1 ± 1 − 8 ( 1 − y 2 )
So, the quantity in root must be perfect square to get t as integer.
After this how to proceed?
@Sharky Kesa , nice solution... from IMO 2006 shortlist.
Good.
Firstly, observe that if ( x , y ) is a solution, then obviously x ≥ 0 and ( x , − y ) is another solution. For x = 0 , we get 2 solutions: ( 0 , 2 ) and ( 0 , − 2 ) .
WLOG x > 0 , y > 0 . Thus, the original statement can be rewritten as
2 x ( 1 + 2 x + 1 ) = ( y − 1 ) ( y + 1 )
which implies that y − 1 and y + 1 are both even, so one of them must be divisible by 4. Hence, x ≥ 3 , and one of these factors is divisible by 2 x − 1 but not 2 x . So
y = 2 x − 1 m + ϵ , m odd , ϵ = ± 1
Plugging this into the original equation, we get
2 x ( 1 + 2 x + 1 ) 1 + 2 x + 1 1 − m ϵ = ( 2 x − 1 m + ϵ ) 2 − 1 = 2 2 x − 2 m 2 + 2 x m ϵ = 2 x − 2 m 2 + m ϵ = 2 x − 2 ( m 2 − 8 )
For ϵ = 1 , we get m 2 − 8 ≤ 0 , so m = 1 , which doesn't satisfy this equation. If ϵ = − 1 , we have
1 + m = 2 x − 2 ( m 2 − 8 ) ≥ 2 ( m 2 − 8 )
which implies 2 m 2 − m − 1 7 ≤ 0 . Hence, m ≤ 3 . However, we already know m = 1 . Thus, m = 3 , so x = 4 . These values indeed satisfy our equation, and we get y = ± 2 3 . Therefore, there are 4 solutions: ( 0 , 2 ) , ( 0 , − 2 ) , ( 4 , 2 3 ) and ( 4 , − 2 3 ) .