Capacitor Exercise (part 3)
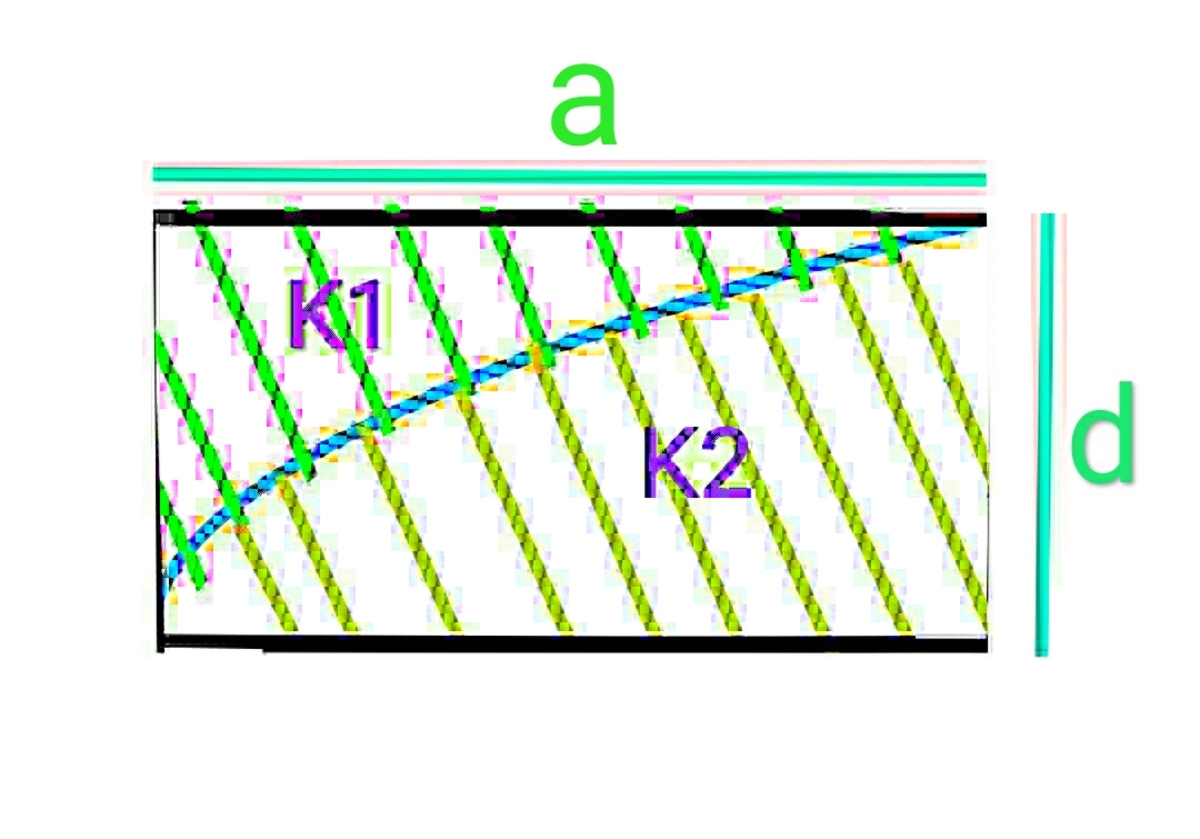
A parallel plate capacitor is made up of two square plates of side
a
, separated by a distance
d
(
d
<
<
a
)
.An imaginary part of the curve
y
2
=
x
is applied as you can see in figure. The upper portion is filled with dielectric of dielectric constant
K
1
and the lower portion is filled with
K
2
as shown in figure. I have provided the view of figure from
−
Y
axis.
 Find the capacitance of capacitor
Find the capacitance of capacitor
Details and Assumptions
1
)
K
1
=
4
2
)
K
2
=
3
3
)
d
=
1
0
4
)
ϵ
0
=
1
5
)
a
=
1
0
0
Everything is in SI units
Assume that the standard formula of capacitor holds.
From now onwards I will tell in each problem that it is original or not as it is a request from a person.
The problem is purely original.
The answer is 3286.89.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase Can we parametrise solid sphere using cartesian coordinates??If yes. Please tell
Log in to reply
In cartesian coordinates:
− R ≤ x ≤ R − R 2 − x 2 ≤ y ≤ R 2 − x 2 − R 2 − x 2 − y 2 ≤ z ≤ R 2 − x 2 − y 2
To check if this works, you could do a triple integral with volume element d x d y d z and see if it yields the proper volume for a sphere
Log in to reply
@Steven Chase I also got the same, but it looks me so weird, so I thought that I am wrong somewhere. Thanks for clarification. Well I decided to make question that a charge is placed at a random position inside anywhere in sphere and find the average field at (2, 0).
@Steven Chase Have a look. Uploaded. I was making one more question . A 1m rod is placed in origin with linear charge density as λ = + 1 . rotating with some constant ω . Calculate the average electric field at ( 1 , 0 , 0 )
Consider a small element from a distance x from the left side of the given diagram of thickness d x . This can be treated as two elementary parallel plate capacitors in series.
d C 1 = y a d x K 2 ϵ o d C 2 = d − y a d x K 1 ϵ o
Since these two elementary capacitors are in series, its equivalent capacitance is:
d C = d C 1 + d C 2 d C 1 d C 2 ⟹ d C = K 2 ( d − y ) + K 1 y a ϵ o K 1 K 2 d x
Now, y = x , and so:
d C = K 2 ( d − x ) + K 1 x a ϵ o K 1 K 2 d x
Plugging in numbers and simplifying gives:
d C = 3 0 + x 1 2 0 0 d x
C = 1 2 0 0 ∫ 0 1 0 0 3 0 + x d x ≈ 3 2 8 6 . 8 9
In your new problem, there is an r 2 in the denominator of the acos argument, where it should be an r . Not sure if that influences the end result
Log in to reply
Nice catch. Corrected now. Apologies for the error.
Log in to reply
Would like to know your thoughts on that problem. I request you to do so, at your convenience. I was reading about relativity and I came across a section on vector transformations. The result of that problem is one that I find strange.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
Sir for the problem electric and magnetic field
α
=
x
,
β
=
y
,
γ
=
z
how can I get the values of
c
1
,
c
2
,
c
3
,
c
4
,
c
5
,
c
6
 I will be happy if you reply Sir
I will be happy if you reply Sir
Thanks in advance! Please reply
Log in to reply
@A Former Brilliant Member – Use the initial conditions.
You can't write the expression for the equivalent capacitance directly. First write the equation as δ C = δ C 1 + δ C 2 δ C 1 δ C 2 = K 2 d + ( K 1 − K 2 ) y a ϵ 0 K 1 K 2 δ x and then pass on to the limit.
@Karan Chatrath Sir, but I reached this expression, and it has terminal velocity also. m L v ¨ + m R v ˙ + B 2 D 2 v = m g R The basic equations are
B D v − I R = L I ˙ m g − I D B = m v ˙ . Please correct me if I am wrong.
Log in to reply
No, you are not wrong. I made an algebraic mistake. Just checked it. My apologies for that.
Also, I noticed that you reached out to me on another social media platform. I do not encourage that, so please do not do that in future. Thanks.
Log in to reply
@Karan Chatrath No problem Sir . Cheers!
My solution, just for fun.