Capacitor Exercise
At a moment
t
=
0
an electron leaves one plate of parallel plate capacitor with a negligible velocity. An accelerating voltage,
V
=
a
t
where
a
=
4
0
0
V
s
−
1
, is applied between the plates . The separation between the plates is
l
=
0
.
0
9
m
. What is the magnitude of velocity of the electron at the moment it reaches the opposite plate?
 Give answer in
S
I
units
Give answer in
S
I
units
The answer is 30543.031.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
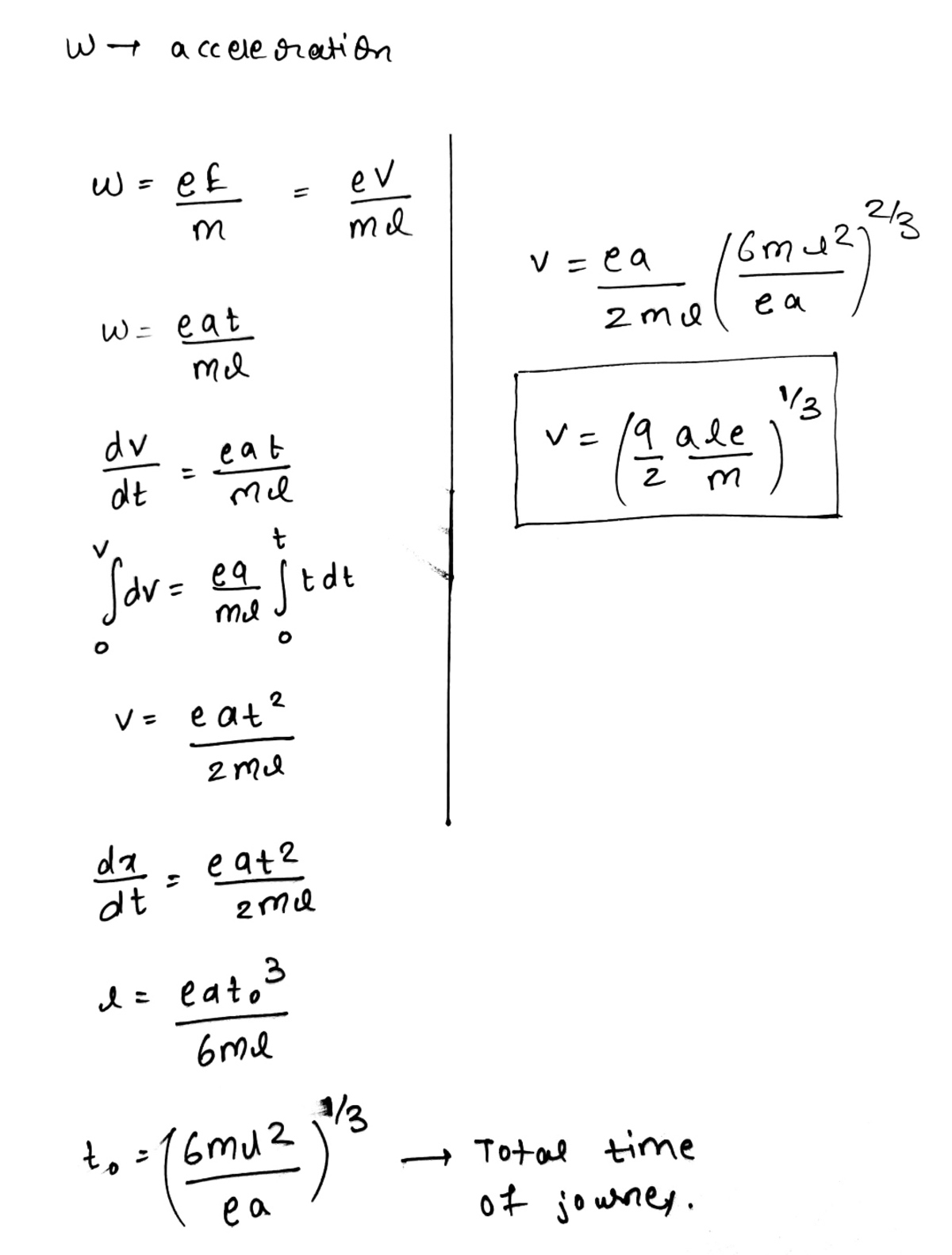
This was a fun problem. Write Newton's Second Law:
F = m x ¨ q E = m x ¨ ℓ q V = m x ¨ ℓ q a t = m x ¨ x ¨ = m ℓ q a t
The second time derivative of position is proportional to the time. This means that the position is a cubic polynomial in time:
x = A t 3 + B t 2 + C t + D
Find expressions for the higher time derivatives:
x = A t 3 + B t 2 + C t + D x ˙ = 3 A t 2 + 2 B t + C x ¨ = 6 A t + 2 B d t d x ¨ = 6 A
The position, velocity, and acceleration are all zero initially. This gives:
x = A t 3
Compare the third derivative expressions at t = 0 :
6 A = m ℓ q a
Resulting in:
x = 6 m ℓ q a t 3
Find the collision time with the final plate ( t f ) :
ℓ = 6 m ℓ q a t f 3
Then plug t f into the velocity equation:
v f = 6 m ℓ 3 q a t f 2
Plugging in numbers gives:
v f ≈ 3 0 5 3 0
Note also that this speed is far below the speed of light (about 1 0 − 4 c ), which means that our Newtonian approach was valid. If the end result had come out to be some significant fraction of the speed of light, we would have had to re-do everything using relativistic dynamics.
I answered this problem in-correctly. I present my approach. Please tell me where I am going wrong.
We have:
E = − d x d V E = − d t d V d x d t E = − x ˙ 4 0 0
Now, The charge of an electron is − e and the equation of motion is:
x ¨ = m x ˙ 4 0 0 e x ˙ ( 0 ) = 0 x ( 0 ) = 0
I proceeded from this point onwards. This equation can be solved analytically. I think the assumption that the electric field is spatially invariant needs scrutiny.
Log in to reply
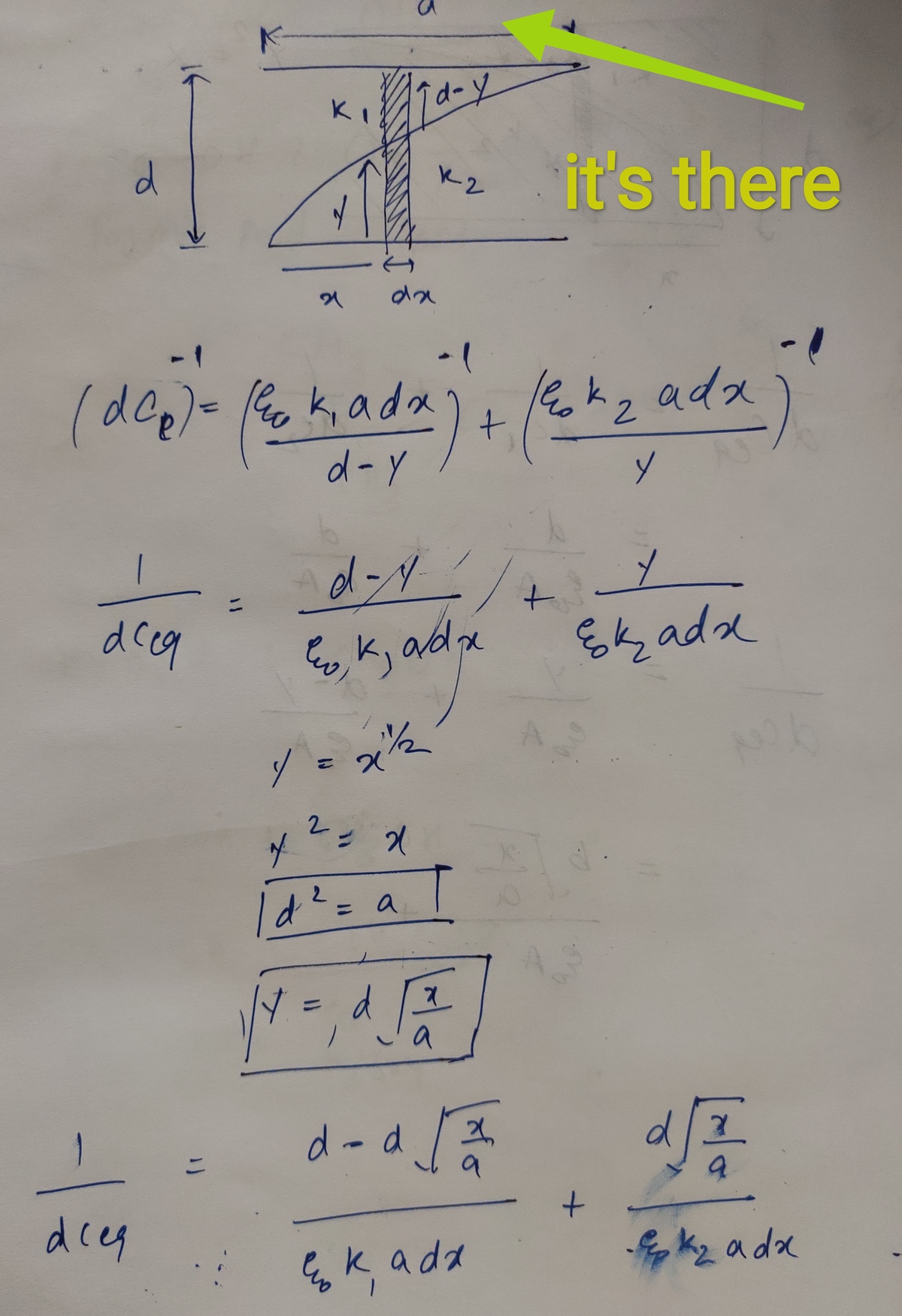
I think you are defining x two different ways: as the general coordinate and as the position of the particle. That's where the problem comes from. The voltage gradient (electric field) has nothing to do with the particle.
Log in to reply
@Steven Chase and @Karan Chatrath I have shared my approach also.
I understand my mistake now. I feel silly. Anyway, thank you for the feedback.
@Neeraj Anand Badgujar thank you for sharing your solution.
Log in to reply
@Karan Chatrath – @Karan Chatrath it is a wire of radius a and electron is projected from its surface. @Steven Chase sir did you feel any ambiguity in the question??
Log in to reply
@A Former Brilliant Member – From which point is it projected? From some arbitrary point on the surface of the wire or from the centre along its axis?
Log in to reply
@Karan Chatrath – @Karan Chatrath From any arbitrary point on the surface of wire
Log in to reply
@A Former Brilliant Member – Thanks for the clarification
@Steven Chase
Sir Please help me in this problem
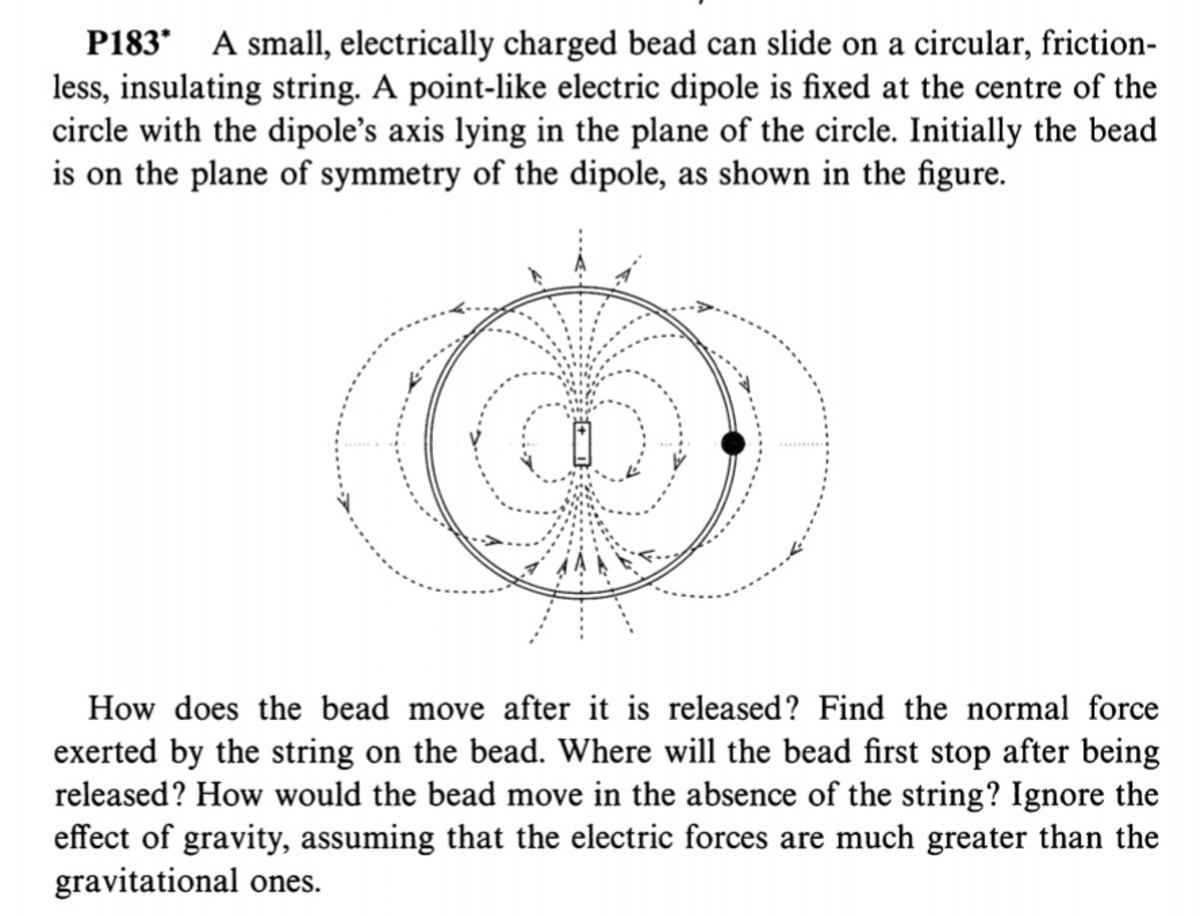
Log in to reply
@A Former Brilliant Member – This would be a good Lagrangian mechanics problem. You can imagine two electric charges at the origin, separated by a small distance. Then you can write the kinetic and potential energy expressions, form the Lagrangian, and solve for the dynamics.
Log in to reply
@Steven Chase – @Steven Chase I don't know Langrangian. But i know Newton's law of motion well.
Log in to reply
@A Former Brilliant Member – Newton will work fine too. You just have to keep in mind that the circular loop screens out the component of the force which is normal to the loop. Only the tangential portion moves the bead.
Log in to reply
@Steven Chase – @Steven Chase Let me try once more. BTW in your questions how do you write details, line by line. For example, in your details and assumptions charge ,mass after each line when I write this it comes to that upper line only???
Log in to reply
@A Former Brilliant Member – Just hit the space bar twice and press enter to make a new line
Log in to reply
@Steven Chase – @Steven Chase Thanks . New problem is uploaded
@Steven Chase – @Steven Chase I have made a new question. A particle(charge q )can have any random position on this plane x 2 + y 2 = 1 find the average field at 2 , 0 .?i have solved this but I don't know my approach is correct or not?? Help
Good solutions, Steven & Karan! My solution closely parallels yours, Steven.