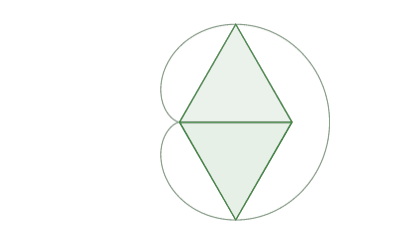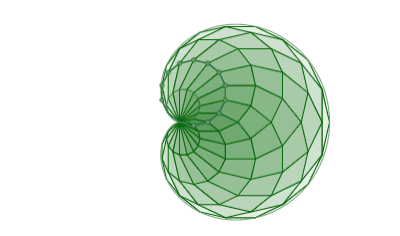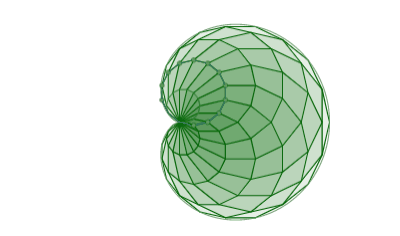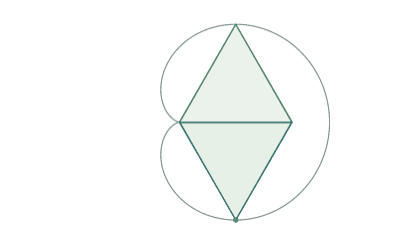
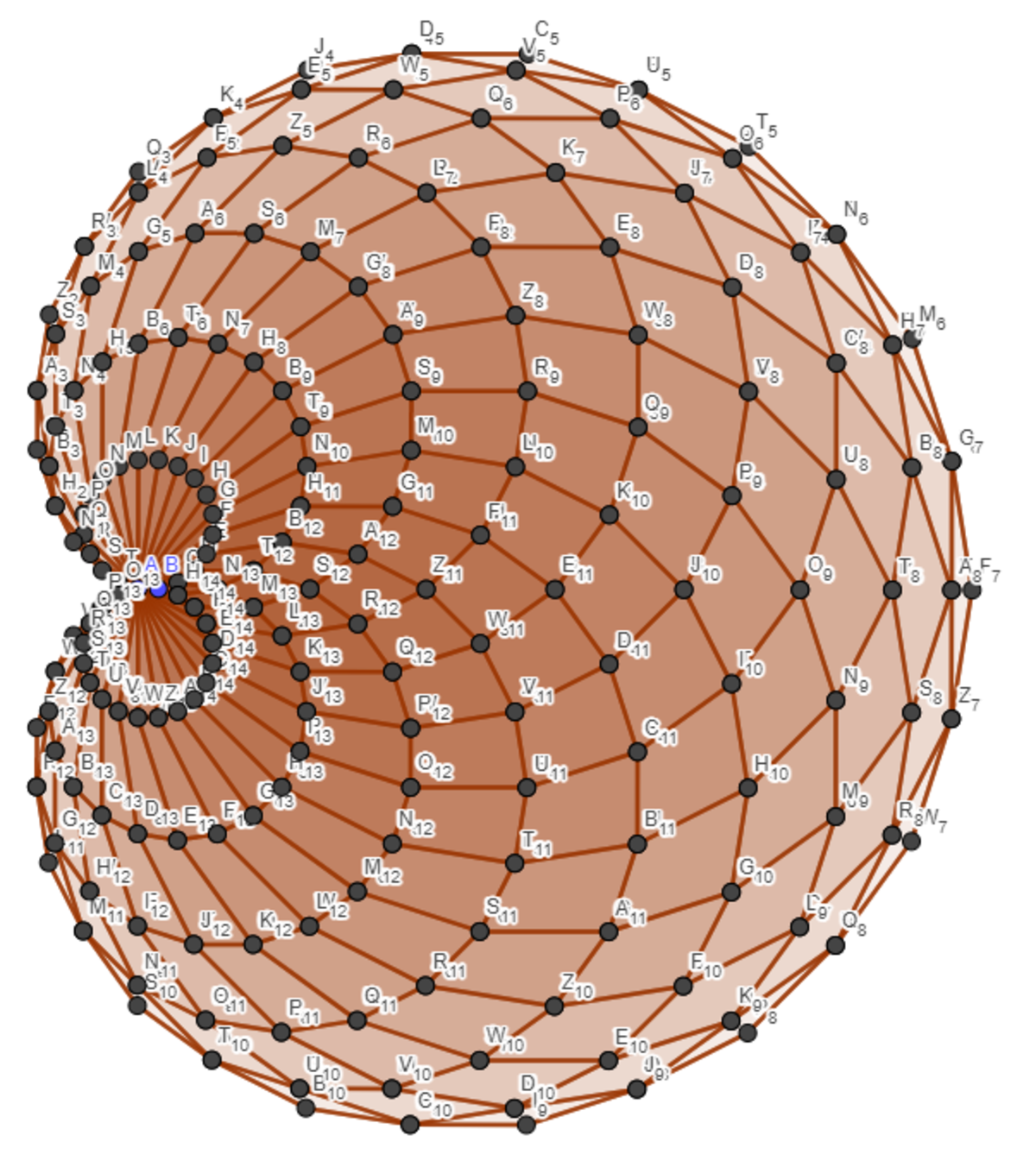
CardioGon

The diagram in the question may remind us that a cardioid can be drawn as the envelope of circles passing through a common point $O$ , whose centres lie on another generating circle also passing through $O$ . (See here , for example.) This suggests that instead of drawing the $n$ -gons, it's a little easier to consider their circumscribed circles.

Let's say the original $n$ -gon has a vertex at $O$ , a vertex at $P_1(1,0)$ , and its remaining $n-2$ vertices $P_2,P_3,\cdots,P_{n-1}$ above the $x$ -axis.

The centroid of this polygon has coordinates $G\left(\frac12,\frac12 \cot\frac{\pi}{n}\right)$ . All of its vertices lie on the circle $\mathscr{C}$ with centre $G$ and radius $\frac12 \csc \frac{\pi}{n}$ .

Consider a point $Q$ on $\mathscr{C}$ . Construct a new $n$ -gon with $OQ$ as an edge (oriented as per the diagram). It's (fairly) easy to show that the circumcircle $\mathscr{C}_Q$ of this polygon has its centre on another circle, $\mathscr{S}$ . Since all of the $\mathscr{C}_Q$ pass through $O$ , by definition, this means the envelope of the $\mathscr{C}_Q$ is a cardioid. The circle $\mathscr{S}$ has radius $a=\frac12 \csc^2 \frac{\pi}{n}$ ; so the area of the cardioid is given by $S(n)=\frac{3\pi a^2}{2}=\frac{3\pi \csc^2 \frac{\pi}{n}}{8}$

As $n$ increases, the approximation of using circumcircles instead of polygons gets better and better; also $\csc\frac{\pi}{n} \approx \frac{n}{\pi}$ so the limit is $\frac{S(n)}{n^4} \to \frac{3}{8\pi^3}$ and the answer we need is $\boxed{14}$ .

---

For fun, if instead of fixing the sidelength of the starting polygon as $1$ we make it $2\sin^2 \frac{\pi}{n}$ , this keeps the cardioids the same size, and we get the following as we vary $n$ :