Castle siege
You are a barbarian invading a castle. Your particular specialty is aiming the catapults. Your catapult, which can launch boulders from the ground at a speed of 5 0 m/s , is 1 0 0 m from the castle wall, which is 1 0 m high. On top of the wall is a castle guard, waggling his fingers at you and yelling "Nyah, nyah, can't get in here!". What angle in degrees with respect to the horizontal should you launch your boulder at so that it hits the guard right between his eyes, which are 1 . 7 5 m above the top of castle wall?
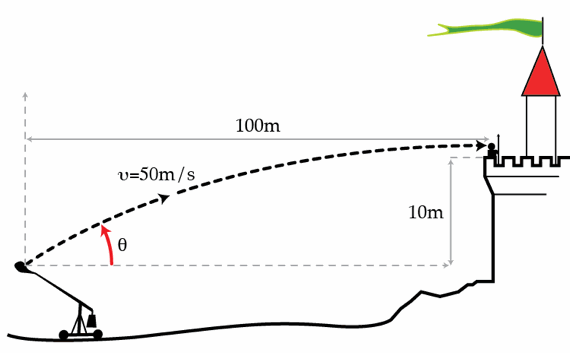
Details and assumptions
- The acceleration of gravity is − 9 . 8 m/s 2 .
- Ignore air resistance.
The answer is 18.55.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Discussions for this problem are now closed
Moderator note:
Yes, we do want the smaller solution as in the picture.
From your initial comment, do you identify more with barbarians :)?
I submitted 78.15
I submitted 78.15
Actually, when the trajectory is a parabola, we can always have two angles for which we get the same range (provided initial conditions are same ) . It is easy to prove that the sum of these two angles will always be 90.
Let us establish an expression for the height of the boulder h in terms of the gravitational acceleration g , the horizontal distance x , the initial speed v and the angle θ , and then solve for θ .
We can decompose the initial velocity of the boulder in a horizontal component v x = v cos θ and a vertical component v y = v sin θ . Since gravity points straight down, the horizontal component of the velocity will remain constant. The time it takes the boulder to cover the horizontal distance x is thus
t = v x x = v cos θ x .
The height of the boulder at time t , given an initial height 0 , initial velocity v y and constant acceleration g is
h = v y t + 2 1 g t 2 = v sin θ v cos θ x + 2 1 g v 2 cos 2 θ x 2 = x tan θ + 2 v 2 g x 2 ( 1 + tan 2 θ ) ,
where I used the identity cos 2 θ 1 = 1 + tan 2 θ . Since we wish to solve for θ , we recognize a second-degree equation in tan θ :
0 = 2 v 2 g x 2 tan 2 θ + x tan θ + 2 v 2 g x 2 − h ,
with the solution(s)
tan θ = g x 2 v 2 ( − x ± x 2 − v 2 2 g x 2 ( 2 v 2 g x 2 − h ) ) = g x 1 ( − v 2 ± v 4 + 2 g h v 2 − g 2 x 2 ) .
When we plug in the numbers g = − 9 . 8 m / s 2 , h = 1 1 . 7 5 m , x = 1 0 0 m and v = 5 0 m / s , we find two possible solutions for θ . In the spirit of the problem statement, we will take the solution with the smallest value of θ , which gives the guard the least amount of time to react:
θ = 1 8 . 5 5 ∘
The other solution is θ = 7 8 . 1 5 ∘ .
From the tarjectory of a particle undergoing projectile motion we have
y = x tan θ − 2 u 2 g x 2 sec 2 θ − − − − ( ∗ )
where x , y are co-ordinates of particle w.r.t launching point, θ is launch angle w.r.t horizontal, g is acceleration due to gravity, u is launching speed.
Given the data we have y = 1 0 + 1 . 7 5 = 1 1 . 7 5 m , x = 1 0 0 m , g = 9 . 8 m s − 2 , u = 5 0 m s − 1 . We need to find θ .
Substituting the values in ( ∗ ) we have
1 1 . 7 5 = 1 0 0 tan θ − 2 × 5 0 2 9 . 8 × 1 0 0 2 × ( tan 2 θ + 1 )
⇒ ( 2 × 9 . 8 ) × tan 2 θ − ( 1 0 0 ) × tan θ + ( 1 1 . 7 5 + 2 × 9 . 8 ) = 0
Solving for θ gives tan θ = 4 × 9 . 8 1 0 0 ± 1 0 0 2 − 9 4 × 9 . 8 − 1 6 × 9 . 8 2
which yields θ = 1 8 . 5 5 ∘ , 7 8 . 1 5 ∘ both of which satisfy the given conditions.
What is wrong with this answer??? h max= u^2 sin^theta / 2g
Final Revised Solution: Set the launching pad as the origin. Since the velocity is 50, the horizontal velocity will always be 5 0 cos θ , since there are no forces acting on the ball's horizontal. Thus, the time it will take the ball to hit the guard is cos θ 2 . Now, the vertical velocity at time t is 5 0 sin θ − 9 . 8 t To find the distance travelled up, we must take the integral of the velocity, since velocity is the derivative of distance. Thus, the distance travelled up at time t is 5 0 t sin θ − 4 . 9 t 2 , as when t = 0 , the expression is equal to 0, which does not affect the integral. Thus, using substitution, we get 1 0 0 tan θ − cos 2 θ 1 9 . 6 = 1 1 . 7 5 . Using Wolfram Alpha, it is easy to find that θ = 1 8 . 5 5 after converting radians to degrees, and we're done.
Since I don't really like any of the other solutions, I'm going to post my solution in this comment (I missed this problem a couple of months ago, so I can't write an official solution) My Solution: Set the launching pad as the origin. Since the velocity is 50, the horizontal velocity will always be 5 0 sin θ , since there are no forces acting on the ball's horizontal. Thus, the time it will take the ball to hit the guard is 5 0 sin θ 1 0 0 , or \frac{2}{\sin{\theta}}. Now, the vertical velocity at time \(t is 5 0 cos θ − 9 . 8 t . To find the distance travelled up, we must take the integral of the velocity, since velocity is the derivative of distance. Thus, the distance travelled up at time t is − 4 . 9 t 2 + 5 0 t cos θ , as when t = 0 , the expression is equal to 0, which does not affect the integral. Thus, using substitution, we get cos θ 1 0 0 − cos 2 θ 1 9 . 6 = 1 1 . 7 5 . Using Wolfram Alpha, it is easy to find that θ = 1 8 . 5 5 after converting radians to degrees, and we're done.
We start by defining the desired height H = 1 1 . 7 5 m and the length L = 1 0 0 m .
The starting velocity v 0 = 5 0 m / s is decomposed into the horizontal direction ( x ) and the vertical direction ( y ) according to the starting angle θ :
v 0 x = v 0 c o s θ
v 0 y = v 0 s i n θ .
Gravity g only acts on the vertical velocity, and so the velocities as functions of time t become:
v x ( t ) = v 0 x = v 0 c o s θ
v y ( t ) = v 0 y − g t = v 0 s i n θ − g t .
Integrating these functions with respect to t gives the distance functions:
D x ( t ) = v 0 c o s θ ⋅ t
D y ( t ) = v 0 s i n θ ⋅ t − 2 1 g t 2 .
When the boulder reaches the position D x = L , the time T will be:
T = v 0 c o s θ L ,
and this is exactly the time when the vertical position must be D y = H :
H = v 0 s i n θ ⋅ T − 2 1 g T 2
or
H = v 0 s i n θ ⋅ v 0 c o s θ L − 2 1 g ( v 0 c o s θ L ) 2 .
By rearrangement, this becomes:
H c o s 2 θ − L s i n θ ⋅ c o s θ = − 2 v 0 2 g L 2 .
We now introduce the substitutions
c o s 2 θ = 2 1 + 2 1 c o s 2 θ
s i n θ ⋅ c o s θ = 2 1 s i n 2 θ .
which transform the equation into:
H c o s 2 θ − L s i n 2 θ = − ( v 0 2 g L 2 + H ) .
In order to solve this equation, we can further transform it by exploiting the general equivalence
a c o s α + b s i n α = c
⇔
R c o s ( α − ϕ ) = c , where R = a 2 + b 2 and t a n ϕ = c b .
For our equation this yields:
R = H 2 + L 2
and
t a n ϕ = − H L ⇒ ϕ = − 8 3 . 2 9 ∘ :
c o s ( 2 θ − ϕ ) = − ( v 0 2 g L 2 + H ) ⋅ H 2 + L 2 1 .
Finally now, inserting the numerical values of the variables, the solution becomes:
2 θ + 8 3 . 2 9 ∘ = 1 2 0 . 4 ∘
θ = 1 8 . 5 5 ∘ .
This problem actually has 2 solutions 18.6 degrees and 78.1 degrees correct?
Yes, I entered 78.15 degrees, it said it was wrong...
I think that since the problem wants the boulder to hit the guard "between the eyes", it has to be 18.55 degrees. Else 78.15 would hit the top of his head.
@Yue Zhang – How do you know the structure of the head of the guard ? W.L.O.G I think both are correct unless specified.
@Yue Zhang – No matter you use 7 8 . 1 5 ∘ or 1 8 . 5 5 ∘ , both are correct and will still hit the guard between his eyes .
From the law of projectile we know that,
y = ( tan θ ) x − 2 ( v cos θ ) 2 g x 2
or, x y = tan θ − 2 v 2 ( cos θ ) 2 g x
where, y= height of the projectile = (10+1.75)m=11.75m
x= distance travelled by the projectile = 100m
g = gravitational acceleration = 9.8 m\s^2
θ = angle to launch the boulder
v = the velocity = 50 m\s
so from the equation above we get
x y = tan θ − 2 v 2 g x × ( cos θ ) 2 1
Let, x y = a and 2 v 2 g x = b
Now the equation becomes,
a = tan θ − b × ( cos θ ) 2 1
or, a = tan θ − b ( sec θ ) 2
or, a = tan θ − b ( 1 + ( tan θ ) 2 ) or, a = tan θ − b − b ( tan θ ) 2
or, b ( tan θ ) 2 − tan θ + ( a + b ) = 0 And with value of a and b
0 . 1 9 6 × ( tan θ ) 2 − tan θ + 0 . 3 1 3 5
By solving the equation we get,
tan θ = 4 . 7 6 6 4 6 and t a n θ = 0 . 3 3 5 5 so, θ = 7 8 . 1 5 or θ = 1 8 . 5 5
The first Value doesn't satisfy our equation.
Hence,
θ = 1 8 . 5 5
v x = 5 0 cos θ is the horizontal component of the velocity.
v y = 5 0 sin θ is the vertical component of the velocity.
h = 1 1 . 7 5 m is the target height.
t h i t is the flight time before hitting the target.
In the horizontal direction we get v x t h i t = 1 0 0 , so t h i t = 2 sec θ
In the vertical direction: h ( t ) h ( t h i t ) 0 = 5 0 t sin θ − g t 2 / 2 = 1 0 0 tan θ − 2 g sec 2 θ = 1 0 0 tan θ − 2 g − 2 g tan 2 θ = 2 g tan 2 θ − 1 0 0 tan θ + ( 2 g + 1 1 . 7 5 ) Using the quadratic formula, tan θ = 4 g 1 0 0 ± 1 0 0 0 0 − 8 g ( 2 g + 1 1 . 7 5 )
Putting this into the calculator and choosing the sign that gives a sensible answer gives us tan θ = 0 . 3 3 5 5 7 1 1 . . . so θ = 1 8 . 5 5 . . . ∘
When dealing with this projectile question you have to component the initial velocity into its vertical ( 5 0 sin θ ) and horizontal ( 5 0 cos θ ) components and deal with them separately:
In the horizontal direction there is no acceleration so there is a constant velocity so you can use s p e e d = t i m e d i s t a n c e The only unknown in this equation is the time and so you end up with the time taken for the projectile flight to be 5 0 cos θ 1 0 0 .
In the vertical direction there is a constant acceleration on the projectile of − 9 . 8 m s − 2 which means that you have to use the equations of constant acceleration (the "suvat" equations). In this scenario, the most appropriate one to use is: s = u t + 2 1 a t 2 You know that the vertical displacement, s, is 1 1 . 7 5 m the initial vertical velocity, u, is 5 0 sin θ m s − 1 , the time taken, t, is 5 0 cos θ 1 0 0 s and the acceleration, a, is − 9 . 8 m s − 2 . When you substitute this into the equation, you get:
1 1 . 7 5 = 5 0 sin θ . 5 0 cos θ 1 0 0 + 2 1 . − 9 . 8 . ( 5 0 cos θ 1 0 0 ) 2
This equation can be simplified by using the trig identity: tan θ = cos θ sin θ
1 1 . 7 5 = 1 0 0 tan θ − cos 2 θ 1 9 . 6
We know that cos θ 1 = sec θ :
1 1 . 7 5 = 1 0 0 tan θ − 1 9 . 6 sec 2 θ
We now need to use another trig identity: sec 2 θ = 1 + tan 2 θ
1 1 . 7 5 = 1 0 0 tan θ − 1 9 . 6 ( 1 + tan 2 θ )
From which you can form a quadratic equation in terms of tan θ :
1 9 . 6 tan 2 θ − 1 0 0 tan θ + 3 1 . 3 5 = 0
This equation can be solved for tan θ using the quadratic formula to give:
tan θ = 4 . 7 6 6 5 and tan θ = 0 . 3 3 5 5 7
From this we can see that the angle needed is:
θ = 7 8 . 1 5 and θ = 1 8 . 5 5
So the answer is:
θ = 1 8 . 5 5
Assuming there is no air resistance, the movement along horizontal axis is uniform, while along vertical axis it is uniformly accelerated.
Writing down the equations for both the motions one gets
{ x = v t cos ϑ y = v t sin ϑ − 2 g t 2
Substituting generic x , y and t for those at the moment of a hit and solving simultaneous equations for ϑ excluding T one gets Y = X tan ϑ − 2 v 2 g X 2 cos 2 ϑ 1 or, reducing all the trigonometric functions to tan : Y = X tan ϑ − 2 v 2 g X 2 ( 1 + tan 2 ϑ ) .
Solving this quadratic equation for tan ϑ , one gets tan ϑ = g X v 2 ± g 2 X 2 v 4 − 1 − g X 2 2 Y v 2 , and ϑ ∈ { 1 8 . 5 5 , 7 8 . 1 5 } ∘ .
For a projectile whose given parameters are the initial velocity v o , vertical and horizontal displacement x and y , the appropriate solution would be
y = x tan θ − 2 v o 2 cos 2 θ g x 2
Substituting the given values x = 1 0 0 m , y = 1 1 . 7 5 m and v o = 5 0 m / s , we get θ = 1 8 . 5 5 ∘ .
How do you get θ from this? It occurs twice on the right hand side.
You start of with y f = y i + v y i t + 2 1 a y t 2
taking y i to be 0, and v y i to be v i sin θ i ,
we can write this as y f = ( v i sin θ i ) t − 2 1 g t 2
then we have x f = x i + v x t
taking x i to be 0, and v x to be v i cos θ i
which can be written as x f = ( v i cos θ i ) t
expressing the equation in terms of t gives us t = v i cos θ i x f
substituting this into the original equation we get
y f = ( v i sin θ ) ( v i cos θ i x f ) − 2 1 g ( v i cos θ i x f ) 2
Simplifying this we get
y f = x f tan θ i − 2 1 ( v i 2 cos 2 θ i 2 g x f 2 )
now we can sub in values. y f = 1 1 . 7 5 m , x f = 1 0 0 m , g = 9 . 8 m s − 2 and v i = 5 0 m s − 1
thus we get
1 1 . 7 5 = 1 0 0 tan θ i − 2 ( 5 0 ) 2 cos 2 θ i ( 9 . 8 ) ( 1 0 0 ) 2
1 1 . 7 5 = 1 0 0 tan θ i − cos 2 θ i 1 9 . 6
we can re-write it as the following
1 1 . 7 5 = 1 0 0 tan θ i − 1 9 . 6 cos 2 θ i 1
as we all know by now, cos 2 θ i 1 = sec 2 θ i
so therefore
1 1 . 7 5 = 1 0 0 tan θ i − 1 9 . 6 sec 2 θ i
as you probably should know, sec 2 θ = 1 + tan 2 θ
1 1 . 7 5 = 1 0 0 tan θ i − 1 9 . 6 ( 1 + tan 2 θ i )
thus we get a quadratic equation in terms of tan θ i
1 9 . 6 tan 2 θ i − 1 0 0 tan θ i + 3 1 . 3 5 = 0
tan θ i = 4 . 7 7 or tan θ i = 0 . 3 3 6
θ i = 7 8 . 2 ∘ or θ i = 1 8 . 6 ∘
(This has nothing to do with the solution but I find this problem hilarious!)
Okay, notice that the displacement of the boulder along the y -axis (upwards) is equal to ( 1 0 + 1 . 7 5 ) m = 1 1 . 7 5 m
And the velocity along the y -axis is equal to v sin θ m/s = 5 0 sin θ m/s .
Let's say that the time it takes for the boulder to hit the guard is t .
So, 1 1 . 7 5 = 5 0 sin θ t + 2 1 g t 2 [ g is the acceleration of gravity].
Or 1 1 . 7 5 = 5 0 sin θ t − 4 . 9 t 2 ⋯ ( 1 ) .
The displacement along the x - axis (horizontally) is equal to 1 0 0 m .
And the velocity along the x -axis is equal to v cos θ m/s .
So we have another equation:
1 0 0 = 5 0 cos θ t [ t is the same t as before]
In other words, t = 5 0 cos θ 1 0 0 = cos θ 2 .
Let's plug this value of t in ( 1 ) .
This is the equation we get:
1 1 . 7 5 = 1 0 0 tan θ − 1 9 . 6 sec 2 θ
⇒ 1 1 . 7 5 = 1 0 0 tan θ − 1 9 . 6 ( 1 + tan 2 θ )
And after a little bit of re-arranging-
1 9 . 6 tan 2 θ − 1 0 0 tan θ + 3 1 . 3 5 = 0 .
Solving this for tan θ gives us two values of tan θ which in turn gives us two values of θ : 1 8 . 5 5 ∘ and 7 8 . 1 5 ∘ .
Both of them happen to be correct although I'm not sure if Brilliant accepts both the answers (you can't submit any more answers after getting the problem right).
The first value of θ implies that the boulder hit the guard before attaining maximum height. The second one means the boulder attained maximum height and as it was falling down(and moving forward at the same time), it hit the guard.
The figure resembles the first scenario. So that's the one I went with.
So, (in my case) θ = 1 8 . 5 5 degrees .