Catch the angle
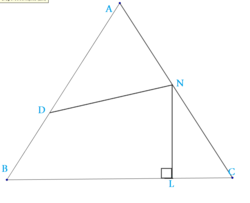 Given the distances
A
C
=
A
B
and
D
B
=
D
N
=
B
C
with
∠
A
B
C
=
8
0
∘
, and
D
N
L
is an acute angle, find the measure of
∠
D
N
L
in degrees.
Given the distances
A
C
=
A
B
and
D
B
=
D
N
=
B
C
with
∠
A
B
C
=
8
0
∘
, and
D
N
L
is an acute angle, find the measure of
∠
D
N
L
in degrees.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
How have solved - sin(30) x sin(80)/sin(50)=sin(40) ?PLS
Please see the attached figure wherein it has been shown that triangle DBN is equilateral. But how may one do this by Euclidean geometry alone?
Sreejato or anyone else, any ideas?
I think we can use a trick: construct equilateral triangle D B N 1 , then prove N 1 is N
Moderator note:
Aways remember that sin x = r tends to have 2 solutions. As such, you would have to explain why one is rejected.
Did the same way but it is too difficult by only euclidean geometry
Log in to reply
what did you use to solve it ??
Log in to reply
I used sine raule in triangles BDC and DNC and got a trignometric equation from which i got 130 and 30 as the value. Taking 30 i came across a contradiction so 130 is the answer.
This question is POORLY worded and the diagram is POORLY drawn. The diagram would lead one to believe that DN slopes upward (when viewed from left to right) as opposed to downward. Therefore, the placement of DN is ambiguous (for the exact same reason why you can't determine a triangle's third side if you are only given Side-Side-Angle). The answer could be either 30° or 130°. Both answers work!! Since DN appears to slope upward (from right to left), I assumed the correct answer was 30° and I was shocked to see I was wrong.
Thank you for poorly drawing the diagram and poorly wording the question. My incorrect assumption cost me 23 ratings points and now my rating for Geometry fell from 2,011 to 1,988, which dropped me from Level 5 to Level 4. I really appreciate this!!! PLEASE REIMBURSE ME AND BRING MY RATING BACK UP TO 2,011!!!
Log in to reply
it can't be 30
Log in to reply
Well, just by looking at YOUR diagram, there's absolutely NO WAY in Hell it could be 130°. In your own diagram, angle DNL is obviously an acute angle, which would strongly suggest 30° instead of 130°.
Because know angle A is 20°, and because we know the length of AD and DN, we therefore have Side-Side-Angle, which leads to ambiguity. Therefore, angle AND can either be 140° or 40°. Therefore, angle DNL can either be 30° or 130°. Because of the way the diagram is drawn, 30° (acute) would look like the correct answer.
Log in to reply
@Desmond Smith – no man ,,, it impossible to be 30 !!
Log in to reply
@Ahmed Moh AbuBakr – That's twice now you've answered me with a simple "It can't be 30". If you want to convince me that it isn't 30°, you're going to have to do a LOT better than that!!
Log in to reply
@Desmond Smith – hhhhh ... wa are not fighting here ... sin(130) isn't equal to sin(30) ... re-think again
Log in to reply
@Ahmed Moh AbuBakr – I have a total and complete understanding of the sine rules, thank you very much. Enough to know that the answer could be either 30° or 130°. If you can't see how the answer could possibly be 30°, then it is your understanding of the sine rules I must question.
I never ever ever said sin(130°) was equal to sin(30°)..... but sin(140°) does equal sin(40°), and that's exactly where the ambiguity lies. Therefore, when you subtract 10° from both answers, you can get either 130° OR 30°. The way the diagram was drawn (with angle DNL looking extremely acute), one would be convinced that it would be 30° instead of 130° (which is obtuse). If you wanted the answer to be 130°, then PLEASE post a better diagram that's more to scale.
Log in to reply
@Desmond Smith – Kk you take angle DNL= 30 then join CD and BN now you get NDC = 110. Further let BN intersect CD at P. So PCN = PNC = 30. This gives PN = PC now further we get PCB = PBC = 50. This gives PC = PB. Now we get PC = PN = .PB and this clearly means NCB = 90 but this is a contradiction as NCB = 80. Hope this would convince you DESMOND SMITH.
Log in to reply
@Akash Deep – Akash, there is an error in your proof:
If angles PCN and PNC both equal 30°, then angle PBC would have to equal 70° instead of 50°. (This is because triangle NBC would have angles of 30° (i.e. angle PNC) and 80° (i.e. angle C). Therefore, the missing angle (i.e. angle NBC (which equals angle PBC)) would then have to be 70°.) Therefore, since triangle PBC would not be isosceles, then PB would not equal PC. Therefore, your argument falls apart at this point.
Ahmed and Akash, we could all have this little dispute settled VERY EASILY with some graph paper, a pencil, a straight edge, and a protractor. Go ahead and draw the triangle in question out for yourselves, as I have done, You will CLEARLY see that you can draw line segment DN either sloping upwards (from left to right) so that angle DNL can be 30° OR you can draw DN sloping downwards so that angle DNL can equal 130°. The proof is in the pudding. You CANNOT beat an actual diagram drawn out correctly. (As I've said before, in the diagram provided in this question, line DN slopes upward, which would lead one to believe that 30° is the correct answer. This is why I was shocked when I submitted my answer and was told that I was wrong when clearly I wasn't.)
PLEASE try drawing out the triangle for yourselves BEFORE your next reply. There is NO POINT continuing this debate when I have clearly proven to myself with actual paper and a protractor (as you can do for yourselves) that I am right. I have the diagram right in front of me as I write this and both 30° and 130° can work as an answer. You can verify this with a protractor once you've drawn the diagram correctly.
So my final question is this... Once you see for yourselves that 30° works as a solution, is it too late to reward me with the points that I lost for getting this question "wrong"?
Thank you
Log in to reply
@Desmond Smith – You are correct answer could be 30 or 130. Reframe the question as sum of possible values of the angle. Thnx to u for initiating the debate DESMOND.
Log in to reply
@Akash Deep – AHMED MOH ABUBAKR , have you drawn out the figure to scale yet to see that I am correct? If so, are you able to adjust the answer so I can get credit for the points that were unfairly deducted from me?
Thanks
Log in to reply
@Desmond Smith – see the first solution in the list
Log in to reply
@Ahmed Moh AbuBakr – Yes, I saw it the first time I came to this answer page last week...... and I DISAGREE with it, which is why we're having this debate in the first place.
(If you look at other comments on this page, you will see that a few other people were unfairly marked wrong as well.)
So I have to ask you again (because you didn't answer me in your last post) ..... Have you drawn out the figure to scale yet to see that I am correct? If so, are you able to adjust the answer so I can get credit for the points that were unfairly deducted from me?
@Desmond Smith – i think you have a misunderstanding in sine rules
You are asking for angle DNL,,,, not angle NDL ! Also, why did you connect D to C,,, which is supposed to be connected to L ! Pls elaborate ?
A non-calculator, non-guess solution.
 Triangle
Triangle
The triangle is an isosceles triangle. Let:
- A B = A B = 1
- D B = D N = B C = x
- θ = ∠ A N D
In △ A B C , by sine law,
sin 2 0 ° x = sin 8 0 ° 1 ⇒ x = sin 8 0 ° sin 2 0 °
Now, in △ A N D ,
1 − x sin θ = x sin 2 0 ° ⇒ sin θ = x 1 − x sin 2 0 ° ⇒ x 1 − x sin 2 0 ° = sin 8 0 ° sin 2 0 ° 1 − sin 8 0 ° sin 2 0 ° sin 2 0 ° = sin 8 0 ° − sin 2 0 °
Using the identity: sin u − sin v = 2 cos 2 u + v sin 2 u − v , we have
sin θ = sin 8 0 ° − sin 2 0 ° = 2 cos 5 0 ° sin 3 0 ° = cos 5 0 ° = sin 4 0 ° ⇒ θ = 4 0 °
We know that ∠ C N L = 1 0 ° because △ C N L is a right triangle.
θ + ∠ D N L + ∠ C N L = 1 8 0 ° ∠ D N L = 1 8 0 ° − θ − ∠ C N L = 1 8 0 ° − 4 0 ° − 1 0 ° = 1 3 0 °
Moderator note:
Aways remember that sin x = r tends to have 2 solutions. As such, you would have to explain why one is rejected (if at all).
you've used the same idea ... pretty
By the figure, considering the triangleDNC:
s i n ( 3 0 ) D N = s i n ( X + 1 0 ) D C ⇒ D C D N = s i n ( X + 1 0 ) s i n ( 3 0 )
By the triangle DBC:
s i n ( 5 0 ) B D = s i n ( 8 0 ) D C ⇒ D C D N = s i n ( 8 0 ) s i n ( 5 0 ) , as BD=DN
So
s i n ( X + 1 0 ) s i n ( 3 0 ) = s i n ( 8 0 ) s i n ( 5 0 ) ⇒ s i n ( X + 1 0 ) = s i n 5 0 s i n ( 3 0 ) s i n ( 8 0 ) = c o s ( 4 0 ) s i n ( 3 0 ) 2 s i n ( 4 0 ) c o s ( 4 0 ) = s i n ( 4 0 )
Or
X + 1 0 = a r c s i n ( s i n ( 4 0 ) ) = 4 0 ° or 1 4 0 °
So
X = 3 0 º or X = 1 3 0 °
Since X is acute, thus X = 3 0 ∘ .