Center Centroid
 A
B
2
+
B
C
2
+
C
A
2
A
D
2
+
B
D
2
+
C
D
2
A
B
2
+
B
C
2
+
C
A
2
A
D
2
+
B
D
2
+
C
D
2
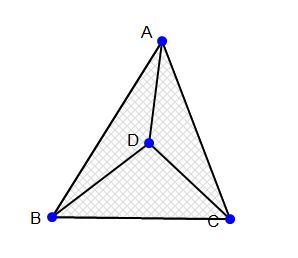
The picture shows a Δ A B C with centroid D . What is the value of the expression above? Give your answer to three decimal places.
The answer is 0.333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Even though your method is better for getting the answer, but what if you had to write the proof that it will be constant for any triangle?
Using Apollonius theorem, we have a result,
3 ( S u m o f t h e s q u a r e s o f t h e s i d e s o f a t r i a n g l e ) = 4 ( S u m o f s q u a r e s o f m e d i a n s )
Now AD, BD, CD are 2/3 of the medians.
The required ratio will be = 4 / 3 [ S u m o f s q u a r e s o f m e d i a n s ] 4 / 9 [ S u m o f s q u a r e s o f m e d i a n s ] = 1 / 3
Let A B = c , A C = b and B C = a . Also, let E , F and G the the intersection points of A D with B C , B D with A C and C D with A B , respectively.
By Apollonius' theorem, we know that:
A E = 2 2 ( b 2 + c 2 ) − a 2
B F = 2 2 ( a 2 + c 2 ) − b 2
C G = 2 2 ( a 2 + b 2 ) − c 2
Also we know that A D : D E = B D : D F = C D : D G = 2 : 1 , so:
A D = 3 2 ( b 2 + c 2 ) − a 2
B D = 3 2 ( a 2 + c 2 ) − b 2
C D = 3 2 ( a 2 + b 2 ) − c 2
Finally, the value that we want is:
9 ( a 2 + b 2 + c 2 ) 2 ( b 2 + c 2 ) − a 2 + 2 ( a 2 + c 2 ) − b 2 + 2 ( a 2 + b 2 ) − c 2 = 9 ( a 2 + b 2 + c 2 ) 3 ( a 2 + b 2 + c 2 ) = 3 1
Log in to reply
http://en.wikipedia.org/wiki/Apollonius%27_theorem
Let m a , m b , m c be the medians on a = B C , b = A C , c = A B of △ A B C . Using Stewart's theorem " m a n + d a d = b n b + c n c ", we obtain 2 a ⋅ a ⋅ 2 a + m a ⋅ a ⋅ m a = b ⋅ 2 a ⋅ b + c ⋅ 2 a ⋅ c , a 2 + 4 m a 2 = 2 ( b 2 + c 2 ) , 4 m a 2 = 2 ( b 2 + c 2 ) − a 2 . Adding this with two similar formulae for m b and m c , 4 ( m a 2 + m b 2 + m c 2 ) = 3 ( a 2 + b 2 + c 2 ) , m a 2 + m b 2 + m c 2 = 4 3 ( a 2 + b 2 + c 2 ) . Since D is the centroid of triangle A B C , A D = 3 2 ⋅ m a , or A D 2 = 9 4 ⋅ m a 2 . Adding this with two similar formulae for B D 2 and C D 2 , A D 2 + B D 2 + C D 2 = 9 4 ( m a 2 + m b 2 + m c 2 ) . It follows that a 2 + b 2 + c 2 A D 2 + B D 2 + C D 2 = m a 2 + m b 2 + m c 2 A D 2 + B D 2 + C D 2 ⋅ a 2 + b 2 + c 2 m a 2 + m b 2 + m c 2 = 9 4 ⋅ 4 3 = 3 1 .
Little more general,
Let ABC be an equilateral triangle of side a .
Hence AD = BD = CD = a^2 by root 3 .
Well I don't know how to write that :(
numerator = a^2 denominator = 3 (a^2) hence numerator / denominator = 0.33
What is this?u're saying when 1:3=0.33333 to write as 0.34 and updated the answer as 0.333,please post answer correctly
1:3 means 1/3 hence 0.33333333333333
Log in to reply
but you have told to "type the ratio upto 2 decimals"
Log in to reply
even when u estimate 0.333 .... u get 0.33 ..... it is not stated there to replace with the succeeding digidt ..... u hav been asked to round off ......
By the way, could someone post the soln for this problem???
Log in to reply
@Ganesh Ayyappan – read the problem its saying if its 0.16666666666666 then type 0.17,so when its 0.333333333 so it should be 0.34
Log in to reply
@Rifath Rahman – It does not matter Brilliant rounds off your answer so there it no need to worry You can even ask @Calvin Lin
@Rifath Rahman
–
0.333 given to 2 decimal places is not 0.34.
0.1666 given to 2 decimal places is 0.17.
Mr u just said to write to 2 decimal places and now or saying different thing.u r not making any sense
Simple Method: Consider ABC as equilateral triangle of side 1 unit. then the calculation becomes simple.