My Take On Champernowne's Constant

Computer Science Level 5

$\large 0.12345678910111213\ldots$

The number above is an irrational decimal number created by concatenating all the positive integers in ascending order, and it is called Champernowne's constant .

Let the $i^\text{th}$ digit of fractional part of Champernowne's constant (base 10) be denoted by $a_{i}$ . Calculate the digital sum of product of all non-zero $a_{i}$ where $i$ is a prime number less than 1000.

Clarification :

The digital sum is sum of all digits of a number. For example, product of $a_i$ where $i$ is prime less than $8$ is $2\times 3\times 5\times 7=210$ . Its digital sum is $2+1+0=3$ .

The answer is 279.

6 solutions

Brock Brown
Mar 18, 2015

Python 2.7:

def is_prime(n):
    if n <= 1:
        return False
    for test in xrange(2,n/2+1):
        if n % test == 0:
            return False
    return True
champ = ''
new = 0
while len(champ) < 1000:
    champ = champ + str(new)
    new += 1
product = 1
for n in xrange(1,1000):
    if is_prime(n):
        print n
        if champ[n] != '0':
            product *= int(champ[n])
print sum([int(c) for c in str(product)])

Christopher Boo
May 21, 2016

Compared to other programming languages, Python is the most convenient one to solve this problem. This is because it doesn't have an upper bound for an integer and it has strong library to deal with conversions between numbers and conversions.

# The fractional part of the Champernowne's constant
S = ""
for i in range(0,400):
    S += str(i)

def is_prime(x):
    if x < 2:
        return False
    tmp = 2
    while tmp * tmp <= x:
        if (x % tmp == 0):
            return False
        tmp += 1
    return True

# list of non-zero digits that has a prime index
l = [int(S[i]) for i in range(1,1000) if is_prime(i) and S[i] != '0']

# product of all digits in l
val = reduce(lambda x, y: x * y, l, 1)

# digital sum
ans = sum([int(digit) for digit in str(val)])

print ans

Pranjal Jain
Mar 17, 2015

def kachra(x):
    b=[]
    while(x!=0):
        b.append(x%10)
        x=x//10
    b.reverse()
    return b
a=[]
i=1
while(len(a)<1000):
    a=a+kachra(i)
    i+=1
def isPrime(x):
    if x<2:
        return 0
    else:
        for i in range(2,x):
            if x%i==0:
                return 0
    return 1
prod=1
for i in range(2,1000):
    if isPrime(i)==1:
        if a[i-1]!=0:
            prod*=a[i-1]

This gives prod= $1329199381429979678084741747997230904228734095362883584000000000000000$ with digital sum= $279$

The product is obviously a huge number. I printed the powers of each divisor and then used wolfram alpha as C++ refused to print all the digits correctly;

#include<iostream.h>
#include<conio.h>

int isprime(int i)
    {
    int r=1;
    for(int k=2;k<=sqrt(i);k++)
        if(i%k==0)
            {
            r=0;
            break;
            }
    return r;
    }

int po(int i)
    {
    int r=0;
    for(;i>=1;i/=10,r++);
    return r;
    }

int main()
    {
    clrscr();
    int i=1,lim,x[10]={0,0,0,0,0,0,0,0,0,0};
    long double prod=1;
    cin>>lim;
    for(long j=1;i<=lim;j++)
        {
        int p=po(j), j1=j;
        for(int h=1;h<=p;i++,h++)
            {
            int d=pow(10,p-h),h1=j1/d;
            if(isprime(i)&&h1!=0)
                x[h1]++;
            j1=j1%d;
            }
        }
    for(int i=1;i<10;i++)
        cout<<i<<" - "<<x[i]<<endl;
    getch();
    return 0;
    }

Raghav Vaidyanathan - 6 years, 2 months ago

As agnishom pointed out, range of data types in c++ is very small for solving such problems. That's why I am moving to python. You may use gmp with c++ to improve range a little bit.

Pranjal Jain - 6 years, 2 months ago

I cannot move to python. I mean, not anytime soon anyway. There are a lot of predefined constructs in python that I think will be really advantageous for a programmer(like functions for permutations). But I have gotten used to C++ and making stuff from scratch. But I will surely learn it after board exam and JEE!

Raghav Vaidyanathan - 6 years, 2 months ago

@Raghav Vaidyanathan – I started learning python 3 days back. Though I still don't know much about different modules

Pranjal Jain - 6 years, 2 months ago

because you do not have a sufficiently large data type in Borland?

Agnishom Chattopadhyay - 6 years, 2 months ago

Firstly, you can optimize your code to run a lot faster by improving upon your isprime function. Secondly, you can store the number as a string , hence the problem of limit of a datatype vanishes.

Karttikeya Mangalam - 6 years, 1 month ago

I agree with you that the isprime function can be made better. But can you please tell me exactly how we can store the numer as a string? We have to multiply huge numbers, so how can we do it with a string?

Raghav Vaidyanathan - 6 years, 1 month ago

@Raghav Vaidyanathan – char num[]="1234"; This is how to treat them as strings. Since, in this problem one of the multiplicand is a single digit integer, it is fairly easy to implement the multiplication function. Otherwise also, you can implement it using either normal multiplication or through Gauss's method. Hence, it becomes fairly easy to manage huge numbers.

Karttikeya Mangalam - 6 years, 1 month ago

@Karttikeya Mangalam – Okay. I get you. Thanks for the suggestions.

Raghav Vaidyanathan - 6 years, 1 month ago

A Former Brilliant Member
May 23, 2016

Python 3.5.1:

from math import sqrt
c = ""
for i in range(1,1000):
    c+=str(i)

def isPrime(n):
    if n==1:
        return False
    else:
        for i in range(2,round(sqrt(n))+1):
            if n%i==0:
                return False
        return True

prod = 1

for i in range(1,1000):
    if isPrime(i) and int(c[i-1])!=0:
        prod*=int(c[i-1])

digitsum = 0
for i in str(prod):
    digitsum+=int(i)
print (digitsum)

Bill Bell
Mar 20, 2015

This problem is slightly more complicated than number 40 on Project Euler. Being rather lazy, I simply adapted code I had already written for use there.

Chuck Jerian
Mar 19, 2015

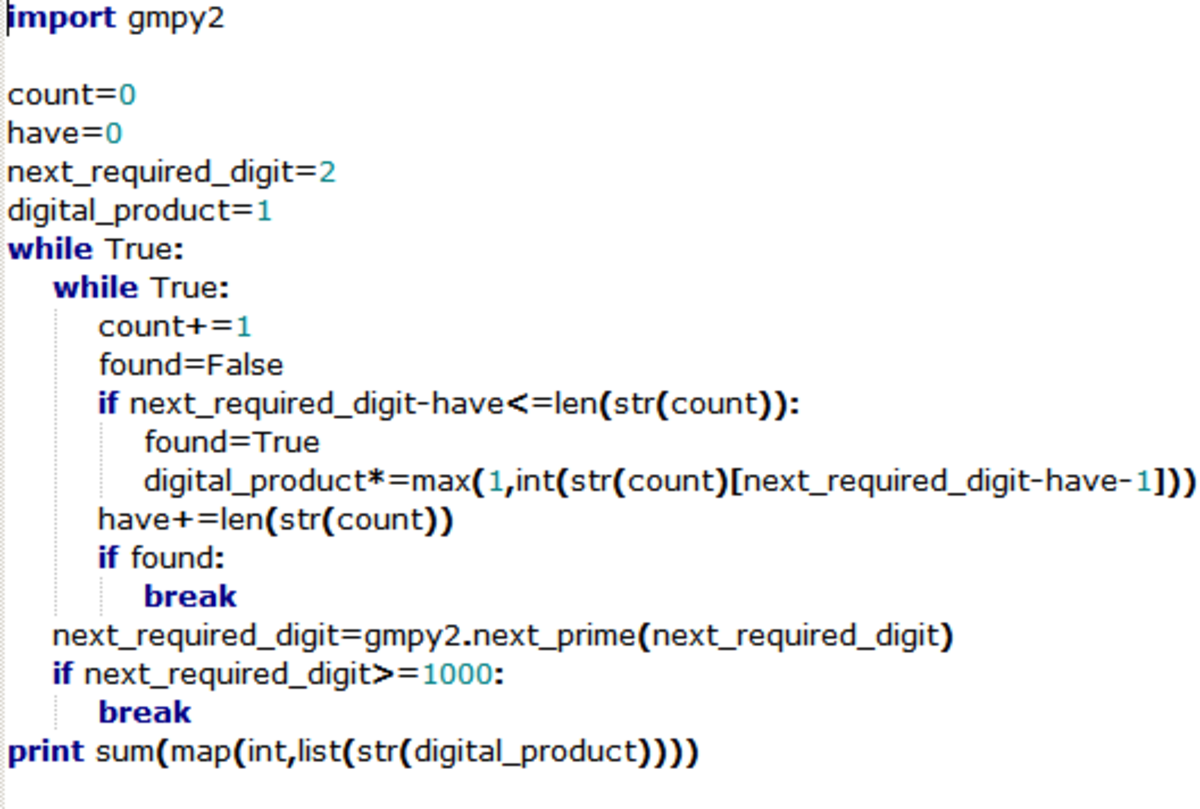
Wrote this in python, got the sieve

    def prime(i, primes):
        for prime in primes:
            if not (i == prime or i % prime):
                return False
        primes.add(i)
        return i
    def historic(n):
        primes = set([2])
        i, p = 2, 0
        while True:
            if prime(i, primes):
                p += 1
                if p == n:
                    return primes
            i += 1
    primes=list(historic(1000))
    primes.sort()
    primes = [p for p in primes if p <1000]
    #print(primes)
    champer =""
    for i in range(1,1000):
        champer += str(i)
    print(champer)
    prod = 1
    for j in primes:
        #champer is numbered from fractional 1 so subtract 1
        cj = champer[j-1]
        #print(j,int(cj))
        if (cj > '0'):
            prod = prod * int(cj)
    print(prod)
    strprod = str(prod)
    dsum = 0
    for c in strprod:
        dsum = dsum + int(c)
    print(dsum)

My Take On Champernowne's Constant

The answer is 279.

6 solutions

0 pending reports