Changing the signs

If we use only $+$ signs, we get the sum of all of the numbers, that is $\frac{9\times10}2=45$

(Using the fact that the sum of all numbers from 1 to $n$ is given by $\frac{n(n+1)}2$ ).

If we switch one of the $+$ signs for a $-$ sign, we subtract $2$ times the number which had its sign switched.

We are therefore only able to subtract even numbers.

The number $45$ is odd.

Subtracting even numbers will never get us to zero.

Let's treat subtraction as addition of the negative of a number. The right hand side is the sum of four even and five odd numbers. Thus it will be odd. QED

For this to be possible, we need to be able to form $\frac{1+2+3+4+5+6+7+8+9}{2}$ by addition of integers $9$ and below.

$1+2+3+4+5+6+7+8+9 = 45$

$\frac{45}{2} = 22.5$ which is not an integer, and so cannot be formed by addition of integers.

(In this context every $\pm$ is independently $-$ or $+$ )

$\begin{aligned} &1 \pm 2 \pm 3 \pm 4 \pm 5 \pm 6 \pm 7 \pm 8 \pm 9 \\ \equiv &1 \pm 0 \pm 1 \pm 0 \pm 1 \pm 0 \pm 1 \pm 0 \pm 1 \\ \equiv &1 \pm 1 \pm 1 \pm 1 \pm 1 \\ \equiv &1 + 1 + 1 + 1 + 1 \\ \equiv &5 \\ \equiv &1 \\ \not\equiv &0 \pmod{2}\end{aligned}$

Meaning that one side of the equation is $0 \pmod{2}$ and the other is $1 \pmod{2}$ , which means that the equation is false.

Hence, the answer is $\boxed{\text{No}}$ .

as we have to use only $+,-$

so, now, $1+2+3+...........+9=45$ and $\frac{45}{2}=22.5$ or not integer.

so, the least possible value of these numbers by using this two signs is= $23-22=1$ .................[ $23+22=45$ ]

so, it is not possible to make 0.

Suppose there is a solution. Take both sides modulo 2, we get $0 \equiv 1 \pmod 2$ . Contradiction.

odd + even = odd odd + odd = even

here's as sort of "pseudo-algebraic" solution: there are 1 more odd numbers than even numbers, so 5odd + 4even = 2even + odd + 1even = 3even + 1odd = odd.

Separate the numbers into groups of odd and even numbers. (1,3,5,7,9) and (2,4,6,8). Look at the even numbers first. No matter how you combine them with + or-, they will ALWAYS sum to an even number.
But there are 5 odd numbers. Hence no matter how you combine them with + or - , they will always give you an ODD number. Odd+Even can never result in zero since zero is effectively an even number. Even more basic, Odd+Even means they are DIFFERENT numbers so by definition can never sum to zero!

If you want it to be zero, all the numbers you add will have to have a sum of the next number that you'll use to subtract. The only one there is 1+2-3. After that the numbers get too high.

Let the sum of all (+) be A and the sum of all (-) be B.
A - B = 0, and A + B = 9×10/2 = 45,
=> A = B = 22.5.
Since A and B can not be natural numbers, the answer is no.

It's simple. Zero is an even number. There are 5 odd numbers in the sequence, so you have to end up with an odd number. QED

They add up to 45, so there's no way to divide that equally so one half cancels the other

Proof by contradiction. Suppose there is a way. Since the sum is equal to 0 this implies all numbers taken away is equal to all the numbers added. Hence, twice the numbers taken away is the addition of all the numbers 1+2+3.....+9. So 1+2+3....+9=2y. However, 1+2+3.....+9=45. So this implies 45=2y where we know y must be an integer. This cannot be true since 45 is odd. Hence, there is no way this can be done.

The sum of all the numbers is 45.

The magnitude of numbers signed to subtract must equal the magnitude of numbers assigned to pluses.

45 is odd, so it can't be evenly distributed between pluses and subtractions.

Therefore equation can't be made true.

... It helps sometimes to prove or disprove a theorem by assuming it is true then work backwards from there and see if it stays consistent. Happy solving!

Since the sum of the digits is odd, I think it is not possible for them to satisfy the given criteria to be proved.

Answer is no

I added the numbers and got 45, an odd number. Unable to divide by 2 and get an integer to somehow keep going and find the right combination. So I concluded that there is no solution.

1 + 9 = 10 2 + 8 = 10 3 + 7 = 10 4 + 6 = 10 remainder 5

Eliminate like pairs (10) and we are left with 5.

For this equation to be true, we must find a way to make two equal sums with the set of digits given, so that one can be subtracted from the other. Each must be equal to half the sum of the entire set of digits. If the sum of all the digits is 45, both sets have to give 22.5. Since this is not a whole number, it is impossible to obtain it through the sum of any set of whole digits. The answer is no.

If we place the positive and negative signs in such a way to make negative and positive tens.

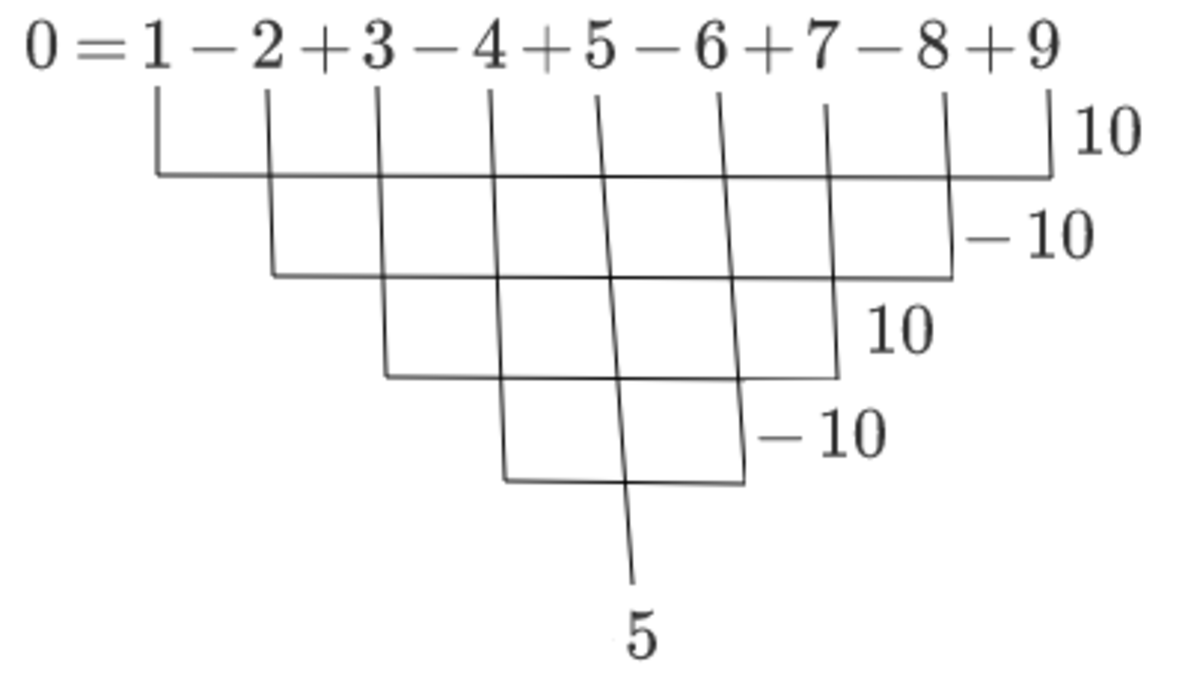
We get $10 - 10 + 10 - 10 + 5 = 5$

We could also end up with -5, but never with zero.

The sum is 45. Now split all numbers to 45 1s (1=1, 2=1+1, 3=1+1+1,...). Let's assign signs. To have a total of zero, the number of -1 should be balanced by +1. This is impossible because 45 is not divisible by 2.