Charged Particle In A Spatially Varying Magnetic Field

Before we start our calculation, let's take a look at the magnetic field. In this flat representation of the field we see that as we move away from the axis, the magnitude of the field grows. Moreover, the field is negative at positive $x$ and positive at negative values of $x$ .

In a magnetic field of constant strength, we expect charged particles to orbit in circles. This doesn't change when the field varies in space. Therefore, as the particle moves into regions of higher field strength, we expect charged particles to to travel in curved trajectories of decreasing radius. Near the $y$ -axis, we expect the trajectory to settle into straight lines.

When the particle crosses the $y$ -axis, the sign of the magnetic field flips so we expect the direction of curvature to flip as well. Thus, the particle should move back and forth across the $y$ -axis, making $\SI{180}{\degree}$ turns on either side as it works its way down the $y$ -axis.

We can generalize fields of this kind a la ${\bf{B}} = -B_0x^n{\hat{\bf{z}}}$ . For $n=0$ we have the classic vertical field of constant strength and we expect the particle to move in circles. As $n$ grows, the magnetic field starts to ramp up in strength more quickly as we venture away from the $y$ -axis, causing the particle to turn around closer and closer to the axis.

The crux of the calculation is the Lorentz force law $\dot{\bf{v}} = \frac{q}{m}\bf{v}\times\bf{B}$ . Writing it out in component form, we have

$\begin{aligned} \dot{{\bf{v}}} &= \frac{q}{m}\bf{v}\times\bf{B} \\ &= -\frac{qB_0x^n}{m}\left(v_x\hat{\bf{x}} + v_y\hat{\bf{y}} \right)\times\hat{\bf{z}} \\ &= -\frac{qB_0x^n}{m} \det \left(\begin{matrix}\hat{\bf{x}} &\hat{\bf{y}} & \hat{\bf{z}} \\ v_x & v_y & v_z \\ 0 & 0 & 1\end{matrix}\right) \\ &= -\frac{qB_0x^n}{m}\left(v_y\hat{\bf{x}} - v_x\hat{\bf{y}}\right) \end{aligned}$

If we let $\alpha = \frac{qB_0}{m}$ and expand the left hand side into component form, we have $\langle \dot{v_x}, \dot{v_y}\rangle = \alpha x^n \langle -v_y, v_x \rangle$ or $\begin{aligned} \dot{v_x} &= -\alpha v_y x^n \\ \dot{v_y} &= +\alpha v_x x^n \end{aligned}$

Now these coupled differential equations are not straightforward to resolve—as we reasoned earlier, the trajectory is some curve who radius changes with distance from the axis. We know that when the particle turns around its velocity is purely in the $y$ direction, so that $v_x=0$ . We also know that magnetic fields do no work (even when they're spatially variant), so $v_y = v_0$ at the point of turn around.

Taking the equation for $\dot{v_y}$ , we have $\frac{dv_y}{dt} = \frac{dv_y}{dx}\frac{dx}{dt} = \frac{dv_y}{dx}v_x$ , so that $\begin{aligned} \frac{dv_y}{dx}v_x &= \alpha v_x x^n \\ \frac{dv_y}{dx} &= \alpha x^n \end{aligned}$ This yields $\begin{aligned} \int\limits_0^{v_y(T)} dv_y &= \int\limits_0^{x_\textrm{max}} x^n dx \\ v_y(T) &= \frac{\alpha}{n+1} x_\textrm{max}^{n+1} \end{aligned}$ which leads to $x_\textrm{max} = \left(\frac{\left(n+1\right)v_0}{\alpha}\right)^{\frac{1}{n+1}}$

We can confirm our qualitative argument about the trajectory of the particle by numerically solving the system for $\langle x,y\rangle$ :

Let the components of velocity of particle along x-axis be v(x) and along y axis be v(y).

Now $\frac{dx}{dt}$ =v(x) and a(y)= $\frac{d{v(y)}}{dt}$

I can resolve the magntic force as: a(y)=Bxv(x)

$\frac{dv(y)}{dt}$ =Bx $\frac{dx}{dt}$

d{v(y)}=Bx(dx)

Integrating both sides to get

v(y)=B $\frac{x^2}{2}$ +c

At t=0 v(y)=o and at the instant when x=x(max) v(y)=v

Solving we get v=B $\frac{x(max)^2}{2}$

Hence x(max)=2

See my solution to the problem A charge in motion.

Putting the given data in the formula obtained for $x_{max}$ , we get

$x_{max}=\sqrt {\dfrac{{2v}_{0}m}{q{B}_{0}}}=\sqrt{\dfrac{2\cdot 2\cdot 1}{1\cdot 1}} =\sqrt{4}=2$

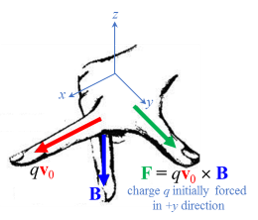
The particle with mass $m$ and charge $q$ is launched from the origin $\textbf{r} = \textbf{0}$ with initial velocity $\mathbf{v_0} = v_0 \mathbf{\hat{x}}$ into a magnetic field $\mathbf{B} = -B_0 x \mathbf{\hat{z}}$ which exerts a force $\mathbf{F} = q \mathbf{v \times B}$ at all times on the particle. When the particle has a velocity $\mathbf{v} = v_x \mathbf{\hat{x}} + v_y \mathbf{\hat{y}} + v_z \mathbf{\hat{z}}$ , by Newton's second law, it will experience an acceleration $\mathbf{\dot v} = \mathbf{a} = \mathbf{F}/m = (q/m) \mathbf{v \times B}$ . Defining $\alpha \equiv q B_0/m$ and substituting in for $\mathbf{v}$ and $\mathbf{B}$ yields: $\mathbf{\dot v} \; = \; \dfrac{q}{m} ( v_x \mathbf{\hat{x}} + v_y \mathbf{\hat{y}} + v_z \mathbf{\hat{z}} ) \mathbf{\times} (-B_0 x \mathbf{\hat{z}}) \; = \; - \alpha \, \mathrm{det} \! \left[ \begin{array}{ccc} \mathbf{\hat{x}} & \mathbf{\hat{y}} & \mathbf{\hat{z}} \\ v_x & v_y & v_z \\ 0 & 0 & x \end{array} \right] \; = \; - \alpha \, (v_y\, x\, \mathbf{\hat{x}} - v_x\, x\, \mathbf{\hat{y}} ) \text{.}$ In terms of components, $\begin{aligned} (1) \; \dfrac{\mathrm{d} v_x}{\mathrm{d} t} &= - \alpha x v_y \\ (2) \; \dfrac{\mathrm{d} v_y}{\mathrm{d} t} &= \alpha x v_x = \alpha \, x \dfrac{\mathrm{d} x}{\mathrm{d} t} = \alpha \, \frac{1}{2} \dfrac{\mathrm{d}}{\mathrm{d} t} [x^2(t)] \; \Rightarrow \; v_y(t) = \dfrac{1}{2} \alpha \, x^2(t) + \text{const and } v_y(0) = 0 = x(0) \; \Rightarrow \; \underline{v_y(t) = \dfrac{1}{2} \alpha \, x^2(t) }\\ (3) \; \dfrac{\mathrm{d} v_z}{\mathrm{d} t} &= 0 \text{, when combined with } v_z(0) = 0 \; \Rightarrow \; \underline{v_z(t) = 0}. \end{aligned}$ These are easier to analyze in reverse order. (3) tells us that the particle's motion is confined to the $x$ - $y$ plane. (2) gives an expression for the $y$ -component of velocity which shows in particular that $v_y \ge 0$ , i.e., the particle drifts only in the + $y$ -direction . (1) shows that, because $v_y$ is always non-negative, the particle is always accelerated towards the $y$ -axis (i.e., towards $x=0$ except when $x=0$ ), and that the restoring acceleration gets larger when the particle tries to get further away from the $y$ -axis. In fact, subbing $v_y(t)$ into (1) gives $\ddot x(t) = - \frac{1}{2} \alpha^2 x^3(t)$ , an equation similar to that for a simple harmonic oscillator except that it has a cubic restoring force versus a linear one - see Note 1. Thus, the particle is expected to reach extreme displacements away from $x=0$ at some $\pm x_{max}$ values before being forced to return.

The value of $x_{max}$ can be determined from energy conservation. Note that $\mathbf{B}$ does no work on the particle because the force it exerts is always orthogonal to the particle trajectory: $dW = \mathbf{F\cdot}\, d \mathbf{s} = \mathbf{F\cdot}\, \mathbf{v} dt = q \mathbf{v \times B\cdot}\, \mathbf{v} dt = q \mathbf{v \times v\cdot}\, \mathbf{B} dt = 0$ . Therefore, the particle's energy at any point on its trajectory is entirely kinetic, $\frac{1}{2} m v^2$ , and equals its initial kinetic energy $\frac{1}{2} m v_0^2 \; \Rightarrow v_0^2 = v^2$ . At extreme $x$ -displacement $x=x_{max}$ , $v_x = 0$ and $v_y = \frac{1}{2} \alpha \, x_{max}^2$ . Since $v_z = 0$ always, $v_0^2 \; = \; v^2 \; = \; v_x^2 + v_y^2 + v_z^2 \; = \; 0 + (\frac{1}{2} \alpha \, x_{max}^2)^2 + 0 \; \Rightarrow \; v_0 = \frac{1}{2} \alpha \, x_{max}^2 \; \Rightarrow \; \boxed{x_{max} = \sqrt{\dfrac{2 m v_0}{q B_0}} = \sqrt{\dfrac{2 \cdot 1 \cdot 2 }{1 \cdot 1}} = 2 \text{ m.}}$

Note 1: The $x$ -motion can be regarded as that of a mass $m$ at the origin connected to a spring exerting a non-linear force of $F_x = -k x^3$ with a spring constant $k = \frac{1}{2} q^2 B_0^2 / m$ . Such a force is conservative and the spring would have potential energy $U(x) = \frac{1}{4} k x^4$ . If the mass at rest at the origin (where the spring is not compressed nor extended) is given an initial velocity $v_0$ , then $x_{max}$ can be obtained by equating the initial kinetic energy to the potential energy when the mass is momentarily at rest at max displacement: $\frac{1}{2} m v_0^2 = K = U = \frac{1}{4} k x_{max}^4$ .

Note 2: Whenever the particle crosses the $y$ -axis, the trajectory is orthogonal to it. This follows because $v_y(t) = \frac{1}{2} \alpha \, x^2(t) = 0$ when $x(t) = 0$ . In this case, $v^2 = v_x^2 = v_0^2 \ne 0$ , so the particle's velocity is a non-zero vector in the $x$ direction when it crosses the $y$ -axis.

Note 3: Considering as Josh did a magnetic field $\mathbf{B} = -B_0 x^n \mathbf{\hat{z}}$ for integral $n \ge 1$ , (2) becomes instead:

$\quad (2') \; \dfrac{\mathrm{d} v_y}{\mathrm{d} t} = \alpha x^n v_x = \alpha \, \dfrac{1}{n+1} \dfrac{\mathrm{d}}{\mathrm{d} t} [x^n(t)] \; \Rightarrow \; \underline{v_y(t) = \frac{1}{n+1} \alpha \, x^{n+1}(t)}$

which, when substituted into (1), changes the $x$ equation of motion as follows:

$\quad (1') \; \dfrac{\mathrm{d} v_x}{\mathrm{d} t} = - \alpha x^n v_y \; \Rightarrow \; \underline{\ddot x(t) = - \frac{1}{n+1} \alpha^2 x^{2n+1}(t)}$ .

Interestingly, for any positive integer $n$ , the force term $F_x = -k x^{2n+1}$ is always restoring since it has odd symmetry in $x$ or, equivalently, the particle moves in an even potential $U(x) = \frac{1}{2n+2} k x^{2n+2}$ . For $n$ even, $\mathbf{B}$ does not change direction for negative $x$ , unlike the original problem where $n=1$ is odd. However, $v_y(t)$ does change direction from $+y$ to $-y$ for negative $x$ . These two changes combine to not only keep the $x$ equation of motion oscillatory but also to cause the trajectory to be an orbit , unlike the drifting "S" pattern trajectory for $n$ odd.