Charge your tablet carefully

The force will accelerate the tablet as well as rotate it. To find the acceleration of center of mass, we can apply newton's second law , according to which, $F_{\text{net}} = m a_{\text{cm}} \\ a_{\text{cm}} = \frac{F}{m}$ The rotation of the tablet can be calculated by finding the torque about the center of mass and using rotational form of newton's second law , which states $\tau_{\text{net}} = I \alpha \\ \tau_{\text{net}} = F \times \frac{l}{\sqrt {2}}\\ I= \frac{1}{6} ml^2$ Therefore, $F \times \frac{l}{\sqrt {2}} = \frac{1}{6} ml^2 \alpha \\ \alpha = \frac{6F}{\sqrt{2} ml} \\$

The motion of point $A$ can be seen as the combination of translation at an acceleration of the center of mass and rotation about the center of mass.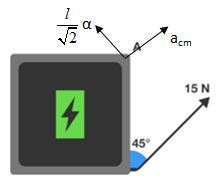

The combined motion will give the net acceleration of $A$ as

$\begin{gathered} a_A = \sqrt {a_{cm}^2 + {{\left( {\frac{l}{{\sqrt 2 }}\alpha } \right)}^2}} \\ = \sqrt {{{\left( {\frac{F}{m}} \right)}^2} + {{\left( {\frac{l}{{\sqrt 2 }}\frac{{6F}}{{\sqrt 2 ml}}} \right)}^2}} \\ = \frac{F}{m}\sqrt {10} \\ = 15\sqrt {10} = \boxed{47.434 \text{ m/s}^2} \\ \end{gathered}$