Checkered Capacitor

Electricity and Magnetism Level 4

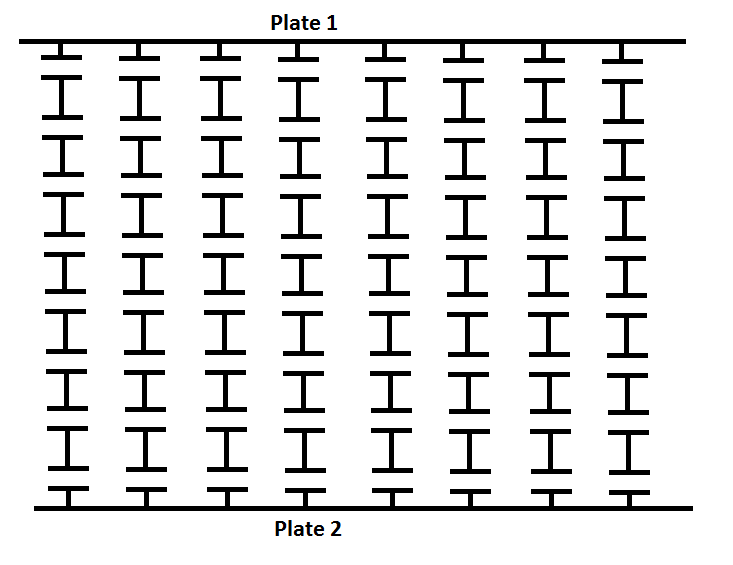
A parallel plate capacitor, with plates $\textbf{A}$ and $\textbf{B}$ of equal dimensions $t \times L$ at a distance of $L$ , is filled with square tiles of dielectric to make a chess-board-like capacitor, as shown in the picture above.

Dielectric constant of the dark tile is $\sigma_1,$ that of the light tile is $\sigma_2,$ and $\epsilon_0$ is the permittivity of free space. All the dielectric tiles are square cuboids of thickness $t$ .

Find the capacitance of this capacitor.

Details and Assumptions:

Assume that the electric field varies between the plates like an ideal parallel plate capacitor.

\dfrac{2\epsilon_0 \sigma_1 L^2}{(\sigma_1+\sigma_2)t}

\dfrac{2\epsilon_0 \sigma_1 L^2}{\sigma_2 t}

\dfrac{\epsilon_0 \sigma_1\sigma_2 t}{\sigma_1+\sigma_2}

\dfrac{2\epsilon_0 \sigma_1\sigma_2 t}{\sigma_1+\sigma_2}

1 solution

Steven Chase
Mar 9, 2017

In general, the formula for capacitance is (where $A$ is the cross-sectional area, $\epsilon$ is the permittivity, and $d$ is the plate spacing):

$\large{C = \frac{\epsilon A}{d}}$

The individual squares have dimension $\large{\frac{L}{8}}$ . Treat each individual square as a capacitor. The cross-sectional area is thus $\large{A = \frac{Lt}{8}}$ . The distance associated with each capacitor is $\large{d = \frac{L}{8}}$ . Thus the capacitance of each square is (when the relative permittivity $\sigma$ is accounted for):

$\large{C = \frac{\sigma \epsilon \frac{Lt}{8}}{\frac{L}{8}} =\sigma \epsilon t}$

Keep in mind that there are two different values of $\sigma$ . Divide the overall checkerboard into 8 columns, each with 8 squares. Each column is equivalent to (4 series $\sigma_1$ capacitors) in series with (4 series $\sigma_2$ capacitors). 4 identical capacitors in series have a capacitance one quarter that of each individual unit. Then the $\sigma_1$ and $\sigma_2$ units in series can be calculated using the general product-over-sum formula for series capacitors. The overall capacitance of a column is given below.

$\large{C_{column} = \frac{\frac{\sigma_1 \epsilon t}{4} \frac{\sigma_2 \epsilon t}{4}}{\frac{\sigma_1 \epsilon t}{4} + \frac{\sigma_2 \epsilon t}{4}} = \frac{\sigma_1 \sigma_2 \epsilon^2 t^2}{4 \epsilon t (\sigma_1 + \sigma_2)} = \frac{\sigma_1 \sigma_2 \epsilon t}{4 (\sigma_1 + \sigma_2)}}$

Capacitors in parallel add. Therefore, the 8 columns in parallel yield a total capacitance equal to 8 times the above value.

$\large{C_{total} = 8 C_{column} = \frac{8 \sigma_1 \sigma_2 \epsilon t}{4 (\sigma_1 + \sigma_2)} = \frac{2 \sigma_1 \sigma_2 \epsilon t}{\sigma_1 + \sigma_2}}$

nice solution !

Sabhrant Sachan - 4 years, 2 months ago

Follow up question: Do all the dark tiles have equal electric field? If yes, what is it? Given that the potential drop across the capacitor is $V$ .

Rohit Gupta - 4 years, 2 months ago

Sounds like a good one. Are you going to post it?

Steven Chase - 4 years, 2 months ago

Are you asking if I am going to post it as a question or am I going to post its solution/answer?

For the solution/answer, I am thinking to wait and let others solve it as well. If no one gives a solution or an answer to this, I'll post one.

Rohit Gupta - 4 years, 2 months ago

@Rohit Gupta – I meant to ask if you would make it into its own problem.

Steven Chase - 4 years, 2 months ago

Interesting. If we had taken 8 rows first, each row would have capacitance $C_{row} = \dfrac{4(\sigma_1 + \sigma_2) \epsilon \frac{L}{8} t}{\frac{L}{8}}$ , and since they are all in series, the total capacitance would be one eighth of this value

$C_{total} = \frac{(\sigma_1 + \sigma_2)\epsilon t}{2}$

Why is this not correct?

Pranshu Gaba - 4 years, 2 months ago

Here's my equivalent circuit. What is yours?

Steven Chase - 4 years, 2 months ago

My equivalent circuit was this:

First parallel, then series.

Edit: I understand now that since $\sigma_1 \neq \sigma_2$ , the electric field across each capacitors in a row won't be equal, so they aren't really in parallel.

Pranshu Gaba - 4 years, 2 months ago

This is a good point you brought up. All the dielectrics in the first row beside the plate $B$ are not in parallel. For the parallel combination, the potential drop across them must be equal. Now, if you consider a dark and a light dielectric, the electric field inside them will be different and hence the potential difference. Therefore, they cannot be considered in parallel.

Rohit Gupta - 4 years, 2 months ago

Awesome problem and solution!:)

Dan Ley - 4 years, 2 months ago

Checkered Capacitor

1 solution

0 pending reports