A chemical gas release
You are analyzing a chemical codenamed H2SO4. You are finishing up the research and, suddenly outside the door, a meteorite hits the containment chamber of H2SO4 and releases it into every room except for the entrance. The power is knocked out but there are spare batteries. They can't last forever, so you have to clean up all of the H2SO4.
Without power, the vents in the building will open and release H2SO4. It is very toxic and will kill everyone on Earth in 15 minutes. Luckily, there is a self-destruct button in each room. Since the system is on lockdown mode, when you exit a contaminated room, it will destroy itself. The building is a square grid as in the diagram.
Every square is a room. You have to enter at the top left corner and exit at the bottom right corner where there is a scrubber to remove the H2SO4. You entered and destroyed all the rooms and survived.
What size is the building in terms of rooms?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
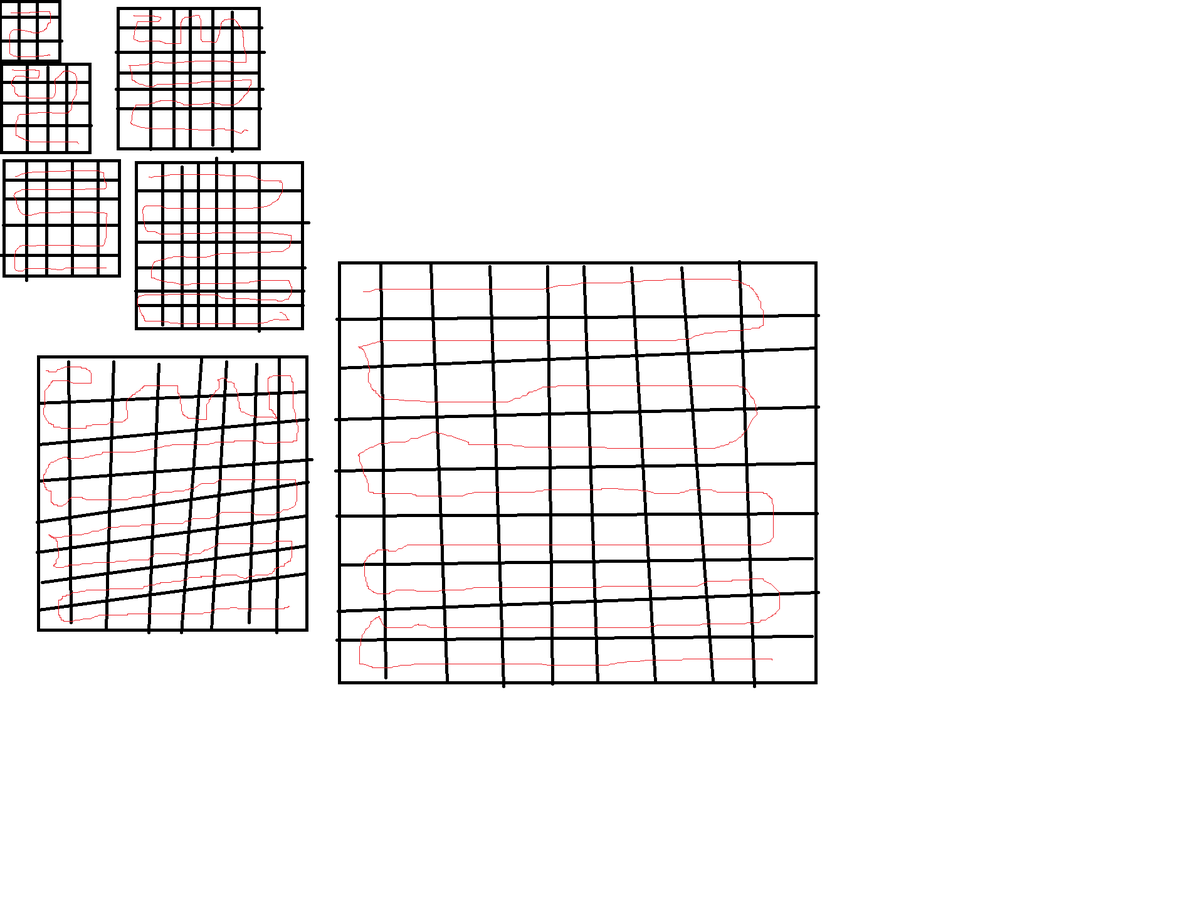
There is something related to this problem called the hamiltonian path problem. A hamiltonian path is a path that touches all points exactly once. A hamiltonian path is possible on all grids of size N but if you have to start and end on opposite corners then it is impossible. You can think of a chessboard.
The two corners are opposite corners. This is the case for any grid with a height and width that are even. Any path between two squares without moving diagonally will alternate between black and white like this. BWBWBWBWBW. And since even*even is even if the path starts on white then it has to end on black and same with white. Odd times odd is odd so you can make a hamiltonian path with odd length and width. But, this is not a hamiltonian path since you can go to the entrance twice since it isn't contaminated. (read the rules carefully) Then, it essentially adds one to the number of squares so it is odd. All of the answers are possible.
