Chess board problem
In an 8 × 8 grid of points, what is the maximum number of points that we can select such that no four selected points are the corners of a rectangle whose sides are parallel to the edges of the grid?
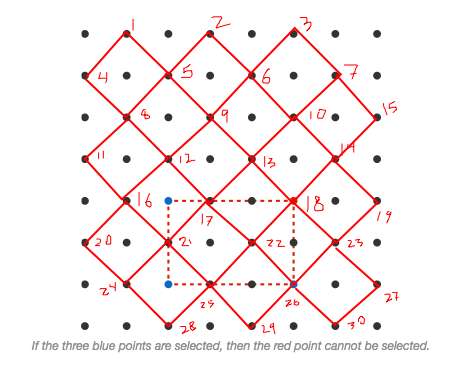
If the three blue points are selected, then the red point cannot be selected.
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Áron Bán-Szabó The wording in the original problem is imprecise, and this can lead people to solving a different problem than intended. The imprecision stems from use of the word "form" in the phrase "colored squares form a rectangle". Used in this way, a reasonable (and I believe most common) interpretation of that phrase is that the rectangles are composed solely of 4 colored 1x1 squares. In fact, what is actually intended for the problem is that the 4 colored squares are corners of rectangles which can be formed or composed of colored and uncolored squares. I wasted two "tries" before figuring out that this was what was meant.
I strongly recommend replacing "no four of the colored squares form a rectangle" with something like "no four of the colored squares can be the corners of a rectangle" or "no four of the colored square centers can be the vertices of a rectangle".
Log in to reply
I have edited the problem for clarity. How does it look now?
Log in to reply
Calvin, I think the problem statement is now accurate, especially with the fig. When I first read your edit last week, I was going to suggest inserting the word "rectangular" as in "8x8 rectangular grid of points" (a rectangular lattice), but the fig now clarifies that. The chessboard aspect of the problem is not explicit as before, but I think folks can still see it there. When I get a chance, I'll update my solution for a lattice.
Good of you to clarify the prob. It's an interesting one, worthy of the effort IMO. If I hadn't spent time figuring out the correct problem interpretation, I wanted to try to prove that that "greedy diagonal packing" algorithm itself was optimal. Perhaps for a future solver!
Wth its not programming.
Log in to reply
Well, you probably mean it's not computer language programming. The origin of the widely-used term mathematical programming actually predates computers and refers to finding a program or plan or schedule - see here or here . Math programming, which is synonymous with mathematical optimization, comes in many varieties - see here . Usually to solve math programs, computer programming is required. FYI, to solve the integer linear program for this problem, I wrote a python program using MIPCL-PY .
The wording is still left for interpretation. It does not require selections to be at 90 degrees from each other. Selecting dots at 45 degree angles would fit the problems description and increase the number of possibilities.
Log in to reply
Would the sides be parallel to the edges of the grid?
I completely misinterpreted the problem thinking that it was the number of combinations of 4 dots that could be selected without forming a rectangle. I painstakingly counted each rectangle and subtracted this from 64 63 62*61/24, getting a nice near 600,000 😂😂😂
I think all solutions are mathematically isomorphic. I mean I'm all solutions there will be one row, and one column with 4 colored points, and one row and column with 2 colored points. You can mix up the rows/columns as much as you want and I'll keep giving you a good solution. That's why I called them isomorphic.
I couldn't figure out a mathematical insight which will give me an answer to an nxn grid :/. Anyone else get something?
Log in to reply
Not quite. 2 solutions are isomorphic if there is a permutation of the rows and columns that send one to the other. For example, looking at the above solutions, we would require that column 6 be mapped to column 7 (only column with 4 dots) and row 1 has to be mapped to row 3 (only row with 2 dots).
While it's obvious that any permutation would lead to another solution, it is not immediately obvious that every pair of solutions can be related by a permutation.
Could you elaborate how the mathematical programming formulation solves the problem? Or perhaps suggest some additional reading on the topic?
Log in to reply
I believe there are powerful algorithms which are designed to solve Integer Linear Programs. You could obtain a solution by feeding your model into them.
Wesley I'm hurting my brain here, couldn't you select two more dots? 2,1 and 1,2 without making any more rectangles?
Log in to reply
If you select (2,1) (2nd row 1st column) in the top diagram, then (2,1), (6, 1), (6, 6), (2, 8) form a rectangle.
Can you show the method for solving the ILP ?
I can't understand the question
We divide the grid into 8 rows. Notice that all of the rows are identical.
We see that we cannot select the same pair of points in any 2 rows, since if we assemble the grid, then among those two rows, the two selected pairs will form a rectangle. Hence each pair of points can be used at most once in all rows.
We see that there are a maximum of 8C2 = 28 pairs of points among all the rows. This means that if we select 3 points in each row, there are a total of 3 pairs of points in each row and a total of 24<28 in all of the rows. We see that we can select 24 points:
∙ ∙ ∙ ∘ ∘ ∘ ∘ ∘ ∙ ∘ ∘ ∙ ∙ ∘ ∘ ∘ ∙ ∘ ∘ ∘ ∘ ∙ ∙ ∘ ∘ ∙ ∘ ∘ ∙ ∘ ∘ ∙ ∘ ∘ ∙ ∘ ∘ ∙ ∘ ∙ ∘ ∙ ∘ ∙ ∘ ∙ ∘ ∘ ∘ ∘ ∙ ∘ ∙ ∘ ∙ ∘ ∘ ∘ ∘ ∙ ∘ ∘ ∙ ∙
It remains a problem that 25 points are impossible. We do a proof by contradiction. By the pigeonhole principle, there must be a column with at least 4 points on it. Looking at the 4 rows that the four points are on, we see that since there must not be 2 identical pairs, by pigeonhole there must be a row with at most 2 points. This is because the seven possible points each form a pair, and among 4 rows, one must have at most one pair, or 2 points.
Among the remaining 7 rows, there are at least 23 points, and at least 2 rows with at least 4 points. We see that those 2 rows share at most 1 point in common. Now notice that among the remaining 5 rows with at least 15 points, there must be one row with at least 4 points, or 5 rows with 3 points.
If there is one row with with at least 4 points, then there are 3 rows with 4 or more points. Since the first 2 share at most 1 point in common, there is at most 1 point that they do not contain. Therefore, the third row must share a pair in common with one of the first two rows, a contradiction.
If there are 5 rows with 3 pairs, then the only place to position a row of three is to have a point shared with each of the rows of four, and a third point on the point that the rows of fours do not share (If the rows of four do not overlap, we immediately have a contradiction). However, after placing 3 rows of 3, we will have exhausted all of the non-overlapped points of the rows of 4 and reached a contradiction
Therefore, the answer is 24 points.
Note: I think you've covered all cases, but it would be clearer if you explicitly specify what is happening in each of the cases, so people can follow you. IE In the "among remaining 7 rows with at least 23 points", I think what you're trying to say is
I cant understand the question
FYI-My answer is incorrect!
Based on the solution already provided, I'm not sure that I understood the problem correctly, but here is what I did.
I drew out some rectangles with sides that are not parallel to the edges of the grid. I then counted up the number of points used to create all of those rectangles and found the answer to be 30.
*Image updated from original.
Ambiguous question I thought.
Log in to reply
The question is: select as many dots as possible without making ANY rectangles (with edges parallel to the edges of the grid). Making rectangles which are diagonal are allowed.
The wording of the problem is perfect, but it's confusing at first.
This took me a half an hour to figure out they were asking something far more simple than I thought.
You misunderstood the problem.
Log in to reply
Thanks. Can you please help clarify it for me then?
As you know, the problem says "the maximum number of points that we can select such that no four selected points are the corners of a rectangle whose sides are parallel to the edges of the grid?"
1) I found the max number of points given my reading of the problem 2) The rectangles I've drawn all use four selected points as their corners, and none of the sides are parallel to the edges of the grid
Looking at the first solution, I see plenty of rectangles with sides that are parallel to the grid so I'm not clear on why that's acceptable. Thanks!
Log in to reply
In the first solution, the "points" that are selected are the 24 squares marked in brown. Can you point out (the centers of) which 4 squares form a rectangle?
The question requires you to find X points, such that no 4 of these X points form a rectangle with sides parallel to the grid. I do not understand how you counted 24 points. If you can highlight them in a particular color, that will help me point out which "4 points form a rectangle".
Log in to reply
@Calvin Lin – I updated my solution for selecting points (instead of coloring squares on a chessboard). Maybe that helps a little.
@Calvin Lin – So, I've updated the picture, and in doing so realized that I missed a few rectangles, and so now I'm getting 30. However, I'm still not clear why the squares that I'm drawing, where their sides are not parallel to the edge of the grid doesn't meet the criteria of the question.
Log in to reply
@Seth Reisner – Hi Seth - the goal of the problem is not to find rectangles, but rather to find a (largest) set of points that are rectangle free , i.e., where no 4 of the points can be used as the corner points of any size rectangle with sides parallel to the grid edges. For example, in your figure, your points { 1 , 2 , 8 , 9 } are the corners of a 2x2 rectangle with sides parallel to the grid edges, so at most 3 of those points can be in a solution. Hope this helps.
Log in to reply
@Wesley Zumino – Thanks so much, now I understand!
@Wesley Zumino – Thanks for helping to clarify! You understood what Seth was doing originally (while I didn't), and that helped you explain the difference in interpretation to him :)
To me the question was non sense, i could not even tell what was being asked.
Points 1,2,9,8 form a rectangle with sides parallel to the original.
I cant understand the question
To verify that this was in fact the maximum possible selected points, I formulated and solved the following integer linear program (ILP), which is a mathematical formulation of the posed problem. Let x i , j ≡ 1 , if point ( i , j ) is selected (blue), and 0 otherwise,
where i ∈ 1 , . . . , R is the row index and j ∈ 1 , . . . , C is the column index of points in a rectangular grid with R rows and C columns.
Then a mathematical programming formulation of this point selection problem is:
subject to: max i = 1 ∑ R j = 1 ∑ C x i , j x i , j + x i , n + x m , n + x m , j ≤ 3 , ∀ i ∈ { 1 , . . . , R − 1 } , j ∈ { 1 , . . . , C − 1 } , m ∈ { i + 1 , . . . , R } , n ∈ { j + 1 , . . . , C } x i , j ∈ { 0 , 1 } , ∀ i ∈ { 1 , . . . , R } , j ∈ { 1 , . . . , C } .
Note: This solution is an update to that originally posted in order to align with the updated problem wording.