Chessboard squares
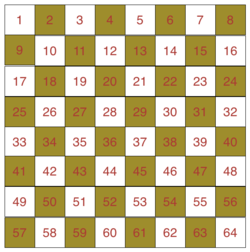 The numbers 1 to 64 are written in order on the chessboard above. What is the sum of the numbers in the yellow squares minus the sum of the numbers in the white squares?
The numbers 1 to 64 are written in order on the chessboard above. What is the sum of the numbers in the yellow squares minus the sum of the numbers in the white squares?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Nice. There are many ways of showing the sum is 0. Let's see how many others the community can come up with.
Log in to reply
Since the number of squares on the chessboard is even this could happen. Isn't it? The problem would be more interesting if set for 7 × 7 chessboard!
Log in to reply
I believe the intention is for this to be an even sided square, and then for people to figure out ways why this is equal to 0. There are many ways to do so. Mine is "any 2 by 2 square clearly has a sum of 0", hence we are done.
Asking if for a 7 by 7 square would make it less obvious, and it then becomes "do this somewhat tedious calculation". Of course, there are ways of speeding it up, by making certain observations. Perhaps, if you post a question for the 101 by 101 square? That would discourage people from finding 1 − 2 + 3 − 4 + . . . , and hopefully inspire them to think creatively.
Log in to reply
@Calvin Lin – Right. Perhaps I can post that. However my only point was that the broken symmetry of the problem (numbers are increasing only in the right direction) makes the answer non-zero when square is odd.
Log in to reply
@Snehal Shekatkar – Yes, that would make a nice question. We can use a similar approach, to pair up the smaller 2n by 2n board, leaving only the edge, which we can easily sum. That will make a nice harder version of this problem.
Log in to reply
@Chung Kevin – The odd number square matrix can be easily done with the help of AP therefore it wouldn't make a tough problem.
@Snehal Shekatkar – Right. The odd case also has a nice generalization.
the numbers in the 1st row of the yellow squares are 2,4,6,8.......which are in A.P then
then Tn = 2n then sum = S(Tn)
sum = n * (n + 1) but n=4 then
sum = 4 * (4 + 1)
sum = 20
the numbers in the 1st row of the yellow squares are 9,11,13,15.......which are in A.P then
Tn = 2n + 7
sum = S(Tn)
sum = n * (n + 1) + 7n n =4
sum = 4 * 5 + 7 * 4
sum = 48
the numbers in the 1st row of the yellow squares are 18,20,22,24.......which are in A.P then
Tn = 2n + 16
sum = S(Tn)
sum = n * (n + 1) + 16n n =4
sum = 4 * 5 + 16 * 4
sum = 84
the numbers in the 1st row of the yellow squares are 25,27,29,31.......which are in A.P then
Tn = 2n + 23
sum = S(Tn)
sum = n * (n + 1) + 23n n =4
sum = 4 * 5 + 23 * 4
sum = 112
the numbers in the 1st row of the yellow squares are 34,36,38,40.......which are in A.P then
Tn = 2n + 32
sum = S(Tn)
sum = n * (n + 1) + 32n n =4
sum = 4 * 5 + 32 * 4
sum = 148
the numbers in the 1st row of the yellow squares are 41,43,45,47.......which are in A.P then
Tn = 2n + 39
sum = S(Tn)
sum = n * (n + 1) + 39n n =4
sum = 4 * 5 + 39 * 4
sum = 176
the numbers in the 1st row of the yellow squares are 50,52,54,56.......which are in A.P then
Tn = 2n + 48
sum = S(Tn)
sum = n * (n + 1) + 48n n =4
sum = 4 * 5 + 48 * 4
sum = 212
the numbers in the 1st row of the yellow squares are 57,59,61,63.......which are in A.P then
Tn = 2n + 55
sum = S(Tn)
sum = n * (n + 1) + 55n n =4
sum = 4 * 5 + 55 * 4
sum = 240
the total sum of yellow squares = 20 + 48 + 84 + 112 + 148 + 176 + 212 + 240 = 1040
yellow squares sum = 1040
then
sum of white squares = sum of the total chess board - yellow squares sum
sum of white squares = ( 64 * 65 )/2 - 1040
sum of white squares = 2080 - 1040
sum of white squares = 1040
i.e
the sum of white squares = the sum of yellow squares then
the sum of white squares - the sum of yellow squares = 1040 - 1040 = 0
even i thought exactly the same way at first instance.....upvoted
Take any small 2x2 square and do as indicated the result is zero, this pattern persist in the whole board. So dividing our 8x8 board into 16. 2x2 miniboard we come out with zero too.
Great observation!
That is not completely true though. Only because the number of squres is even, this could happen. Try it!
Log in to reply
You are correct I assumed otherwise the number of yellows and whites will be unequal.
A pattern of two by two squares is ALWAYS even.
I saw it too but more obvious is the difference between 2 consecutive integers is is 1.
Of course, I did it a harder way by noticing a column equals 32 or -32 depending on the colour that starts. I only had to add up one column because each square as you go down is 8 more than the previous square. That means if you start from the top, the 2nd colour will have 8 more per square. of that colour. Since there are four of each colour in a column, the 2nd colour in each column will have 8x4 value more than the colour that starts.
Great observation!
oh wow. I was not aware that the columns summed up so nicely. Thanks for sharing.
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
easy, we gonna subtract the yellow square to the white square
in the first row :
2 − 1 = 1 , 4 − 3 = 1 , 6 − 5 = 1 , 8 − 7 = 1
for the second row :
9 − 1 0 = − 1 , 1 1 − 1 2 = − 1 , 1 3 − 1 4 = − 1 , 1 5 − 1 6 = − 1
so, we got 4 in the the even-numbered row and -4 in the odds-numbered row
and since there's equal even-numbered and odds-numbered row, so the answer is 0
WE Added fist two rows white squares and also the yellow squares and subtracting the sums,it is ZERO.Same will apply for other rows as well. Therefore answer is ZERO.
It is a 8 * 8 Square Matrix, , We can think of it as Sum of sixteen 2 * 2 square matrices,, Now in each 2 * 2 matrix at top row yellow wins with 1 point, and at bottom row white wins with 1 points,,, Ultimately no one wins, the game ties.
Nice way of thinking about it
Lets add the numbers seperaratly so hat it would add to 65. Since there is the same amount of white and black squares, the answer is 0.
Count the yellow squares. The answer should be 32. Then count the white squares. The answer also should be 32.
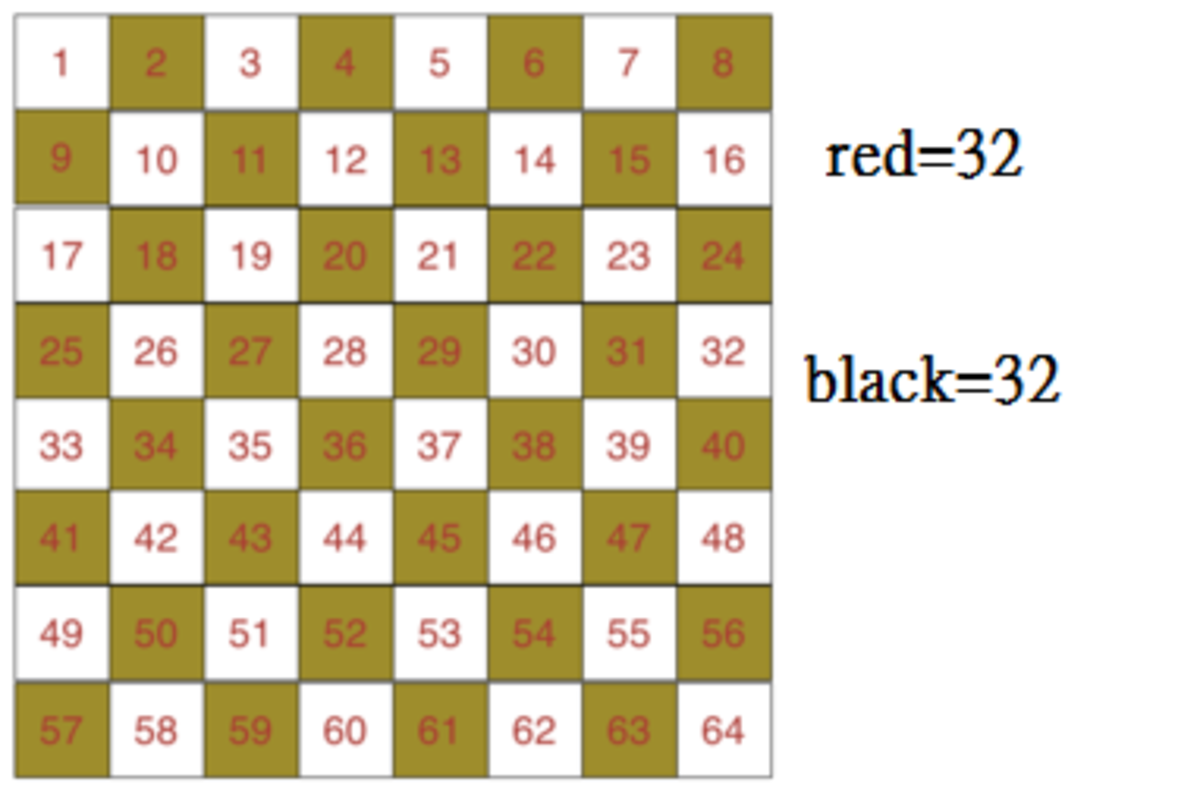
Then do the simple math. The answer is 0.
I just add them all up and then subtracted.
Sum(yellow squares-white squares) of first row from top is =4, Sum(yellow squares-white squares) of second row from top is=-4, Sum(yellow squares-white squares) of 1st row and 2nd row fro top=4-4=0.
Similarly, Sum(yellow squares-white squares) of 3rd and 4th row from top=0,Sum(yellow squares-white squares) of 5th and 6th row from top=0, & Sum(yellow squares-white squares) of 7th and 8th row from top=0. Therefore the answer is '0' (zero)
This is much easier than the column totals
Half are white, half are brown. There are 32 of each. Thus subtracting them gives you zero.
Using Summation for Arithmetic series:
Sum of White boxes= 1/2 * 32 * (1 + 64) = 1040
Sum of Yellow boxes = 1/2 * 32 * ( 2 + 63) = 1040
Hence 1040 - 1040 = 0 (ANS)
I would say this is the most logical yet easiest to understand proof.
My apologies. This "proof" is actually flawed because the numbers in both the series do not follow a regular pattern. e.g. number in first series are 1 3 5 7 10 12 ... which actually is not an arehtimetic series
Let's say that we add diagonally opposite squares... 6 4 + 1 = 6 5 , 6 3 + 2 = 6 5 , 6 2 + 3 = 6 5 , 6 1 + 4 = 6 5 , and so on and so forth... All diagonally opposite squares have the same sum. And since there's an equal number of white and yellow squares, we can say that the answer is 0 .