Choose Your Goblet
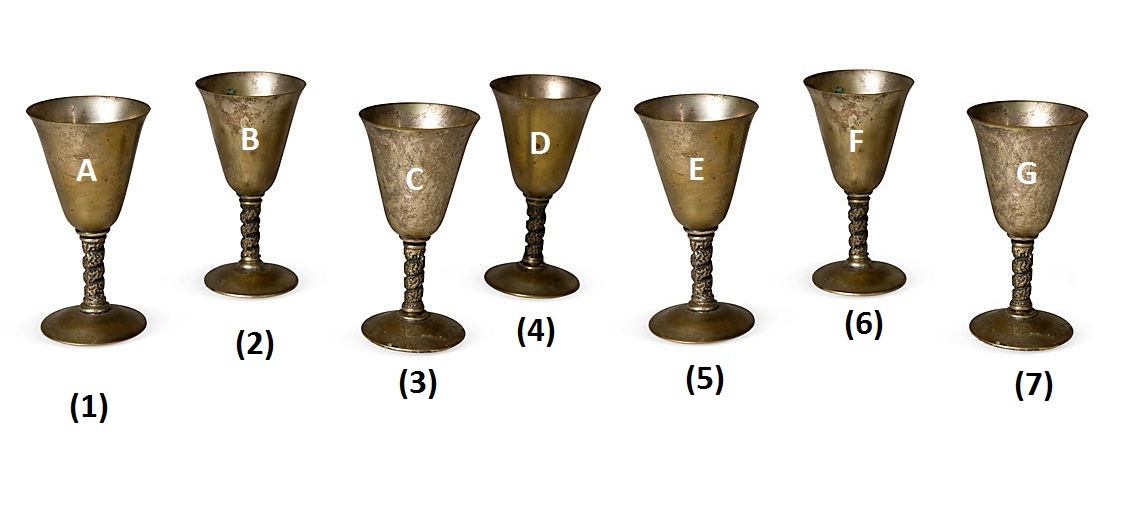 One of the seven goblets above is made of real gold. If you start counting at A and wind back and forth while counting (A, B, C, D, E, F, G, F, E, D, ...), then the golden goblet would be the
1
0
0
0
th
one that you count.
One of the seven goblets above is made of real gold. If you start counting at A and wind back and forth while counting (A, B, C, D, E, F, G, F, E, D, ...), then the golden goblet would be the
1
0
0
0
th
one that you count.
Which one is the golden goblet?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
24 solutions
How and why? Why to use 4(mod 12) ?
Log in to reply
In order to find the 1000th goblet, you can figure out how many times you go through the process by counting how many times it takes you to come back to the first goblet. Here, it is 12 goblets to get back to the 1st. Now if you want to figure out which one you will end on at 1000, you can divide 1000 by 12. It leaves you with a remainder of 4. Therefore, 4 from the 1st one will give you the 1000th one. If you were trying to find the 1002nd one, you'd divide 1002 by 12, and it would be the 6th one.
Log in to reply
Hello Ryan, your reply helped me a lot. But I have a query.
We were at goblet A when we reached the 996th goblet (as remainder left is 4). So shouldn't the 1000th goblet be E?
Log in to reply
@Vanya . – No, we were at goblet B when we reached the 996th goblet, since we have just completed one period more, and B is the last goblet in the period, not A. Note, as an example, that the 12th (and in general, the 12n goblet for n integer) is goblet B. As 996 = 12 × 83, 996 is goblet B
7*X-(X-1)=1000 6X+1=1000 X=166.5 so here , odd rotation ends with G and even rotation starts with A . 166 ends with A 1 rotation represents A --G or G--A 0.5 is the middle goblet of the count and its D
goblet A=25, B=50 C=75 D=100 thus with increment of every 25 we move to the next goblet hence goblet D is the 1000th. ie goblet 4.
Log in to reply
7 x 70 is 700 7 goblet means that it starts back at a then 7 x 35 plus 700 is 1005 witch end in g count back 5 to make 1000 = c
You should not have marked the answer in the picture. There D is coloured a bit blackish than others.
Log in to reply
yeah I didn't even look at that one but nice observation
7*X-(X-1)=1000 6X+1=1000 X=166.5 so here , odd rotation ends with G and even rotation starts with A . 166 ends with A 1 rotation represents A --G or G--A 0.5 is the middle goblet of the count and its D
I didn't know how to post this , they were asking to do in some software or something
If you need 12 steps to get from A back to A, 1000%12 = 4: after 83 times looping you get back to A (count 996). Remainder is 4, so you need to take 4 extra steps, which brings you to goblet E ? Do I see this wrong?
Log in to reply
I got stuck here as well. The remainder does indicate the extra steps, but A is the first step. It's easier to think of the remainder as the position. To see it clearer, let's make 13 as the golden goblet's position. We would evaluate it;
13 ≡ 1 (mod 12)
This is saying that the remainder of 13 ÷ 12 is 1.
Using A as the 0th step would mean the B is the Golden Goblet in our new example. But counting the 13 goblets made it more clear to me that the A is the first step and not the "0th" step and the B is the last step (nth step where n ≡ 0 (mod 12)).
you can see which is gold
@Alan Li Yes, I just saw that 4 was different and picked that one!
confusing to me
Easy and very simple.
Log in to reply
what is mod 12
Log in to reply
Mod is simply reminder you get when divided by a number N. Here the number is 12 --so MOD 12
- Observe the pattern repeats from A to G and back to B *
- Realise that you count 12 times from A to G and back to B
- 1000/12 = 83 r 4
- Count 4 from A --> leading you to D, answer 4 :)
*Common error: you don't go back to A, or else you will have two A's i.e. A,B,C,D,E,F,G,F,E,D,C,B, A,A
good work! :)
We don't have 2 A's or others. ..plz correct it.
Why shouldn't we have two A's
I still don't understand how you count 12 times from A to G. And back to G, Why?
*Back to B rather.
if we write down the sequence (1,2,3,4,5,6,7,6,5,4,3,2,1,2,3,4,...) we notice that the first number repeated at the 13th number, therefore there is a cycle of 12 numbers repeating. So, 1000 ( mod ) 12 =4. as a general form , we can write 12(k)=0, 12(k)+1=1 , 12(k)+2=2 . . . 12(k)+12=2.
1,2,3,4,5,6,7,6,5,4,3,2 and now a can't come at last because after this pointer will be point to starting location who is 1; so answer is 1000(mod12) = 4
Layman solution:
Count 6 from the left. Then count 6 from the right. Then count 6 from the left. And so on. In this way you always count 6 but you land (after a count of 6) at one of two critical goblets every time (2 and 6).
6 1 0 0 0 = 1 6 6 . 6 . . . You can only make 166 repeats of 6 counts, ie. 1 6 6 × 6 = 9 9 6 counts.
As 166 is an even number, the critical goblet will be 2. Try doing the 6 counts, you will find that after every oddth group of 6 counts you land on 6 and after eventh group of 6 counts you land on 2.
You have made 996 counts. You need 4 more. So starting from goblet 2, four more brings you to 1, 2, 3, then 4. The 1000th count lands on goblet 4.
I did 6 also for counting one way, 12 also works if you count full cycles.
That's exactly what I did
Simplest possible way of solving: count the glasses back and forth, until you've counted to ten. To every power of ten you've counted, that glass, in this case, Glass D, will be the one you're on. Since 1000 is just 10 to the power of 3, D is the answer.
Why is this observation true?
It is certainly not true for powers of 2 landing on Glass B.
yeah this is much simpler and easy and takes less time
your method will not work if there were 8 goblets and 100 steps or 10000 steps so on....
The way I did it is :: The first time you go across the row (A,B,C,D,E,F,G), there are 7 numbers. But, since you don't count A or G twice before going back across the row, the remaining times you go back and forth there are only six numbers.
1000-7 for the first row = 993 993/6 numbers per row = 165.5
This means that you go back and forth 165 times, and the gold goblet is halfway across the next row, or 3 goblets from the end goblet, or goblet D.
I did the same except last step. I considered back and fort 166 times ,landing on goblet G. Then, 166x6 +7 = 1003 ,means G is 1003th goblet.
Wow, I forgot about the winding back and forth part and I did 1000 = x mod 6 but I still got x as 4. Is there a reason why its the same answer or is it just simple coincidence?
The numbers we can get for A are: 1, 13, 25 ... =1(mod12) the numbers we can get for B are: 2, 12, 14, 24 ... =2(mod12) or 0(mod12) the numbers we can get for C are: 3, 11, 15, 23 ... =3(mod12) or 11(mod12) the numbers we can get for D are: 4, 10, 16, 22 ... =4(mod12) or 10(mod12) the numbers we can get for E are: 5, 9, 17, 21 ... =5(mod12) or 9(mod12) the numbers we can get for F are: 6, 8, 18, 20 ... =6(mod12) or 8(mod12) the numbers we can get for G are: 7, 19, 31 ... =7(mod12) 1000= 12x83+4 = 4(mod12) the answer is D
A-------B-------C-------D-------E-------F-------G
1-------2--------3-------4-------5-------6-------7
13----12-------11-----10------9-------8-------X
X------14-------15-----16-----17-----18-----19
25-----24-------23-----22-----21-----20------X
..............
..............
subtract 1st 7 count => 1000-7 = 993 count remains.
after 1st row, each row contains 6 counts backward and forward alternatively.
=> 993/6 = 165.5 = 165 + 0.5
165 is odd
odd < 165.5 < even
=> backward complete and middle of forward counting.
now 0.5x6 = 3
3rd count while forward progress is D
=> D => 4
check:
D goblet count series is 4, 6, 16, 22, 28, .....
=> n-th term is 6n−2
=> 6n−2=1000 => n = 167
which is an integer => ok (Checked)
First you go to
7
t
h
g
l
a
s
s
. That is
G
Now after
6
step you will go to
A
And again
6
step ,again 7. Then
1
0
0
0
=
7
+
6
k
+
s
o
m
e
t
h
i
n
g
. Here
k
=
1
6
5
→
o
d
d
,
a
n
d
,
s
o
m
e
t
h
i
n
g
=
3
Which means
A
and then it will go
3
step which comes to
→
D
The material used to make D is visibly different oops
Since I didn't know the formula pertinent to this problem, I counted for the case of 10 and got D. Then I counted for the case of 100 and got D again. I believe D would be the answer for all powers of 10 greater than 0.
If you count one loop, you find that each cup occurs once every 12 counts. Using this, I would try goblet A, the resulting equation being 1+ 12*X with X being a random number. I try this until X = 83 results in a value of 997. I count the remaining B=998, C=999, so D = 1 0 0 0 (which is the golden goblet).
Oh boy, this is my chance to strike it rich! I don't have the time to count 1000 times, though, so I need another solution.
Luckily for me, after every 12th goblet counted, the counting restarts at goblet 1. The largest multiple of 12 that is at most 1000 is 996 , so we know number 997 will be goblet A . Therefore, I only need to count four goblets and run away with my prize!
And just like that, goblet D is revealed to be pure gold . Now, this better sell for some big money.
We can take here modulo 7 to make the solution.First see that if here was mentioned the 16th goblets we can write this as, 16=7 * 2+2.And the goblet will be (2+2)th or 4th goblet counting from the front side(taste it yourself).But if it was mentioned 9th goblet,where 9=7 * 1+2,the answer would be (1+2)th or 3th from the back side.Why?Because here the quotient is odd(1).So if K=7 * a+b where a is even, the K th goblet will be the (a+b)th goblet counting from the front side and when a is odd the Kth goblet will be the (a+b)th goblet counting from the back side. Now come to the point,1000=7 * 142+6.So the goblet will be the (142+6) or 148th goblet. We can do the same thing again,148=7 * 21+1.So the goblet will be the (21+1)th or 22th goblet.Note that here we don't need that the goblet is conting from where because we haven't reach the solution yet.Finally 22=7 * 3+1,so the goblet will be the (3+1)th or 4th goblet.The solution will remain same if you count it from front or back side. So the goblet will be the 4th goblet.
first and last goblet always follow the pattern 6x + 1, first goblet when x is even, while it's last goblet when x is odd. observing first integer dividable by 6 before 1000, it's 996. The x would be even. So the first goblet follows the same pattern and it's 997. It follows B = 998, C=999, D=1000
A more intuitive solution: First we write down the goblets: A B C D E F G The we write the numbers that ends up on each of them when we count them as the problem says A B C D E F G 1 2 3 4 5 6 7 13 12 11 10 9 8 14 15 16 17 18 19 We notice that goblets A, C, E and G will always have an odd number, and since 1000 is even we can rule them out. Then we can see that the numbers of goblet D increase by 6 every time. Since the starting number for goblet D is 4, we need 996 more to reach 1000, and since 9 9 6 ≡ 0 ( m o d 6 ) We find out that goblet D will be the 1000th
Easy sol: This has a cycle 12 and it repeats this means that we can use modular arithmetic
1 0 0 0 m o d 1 2
we just need the remainder because its like we've counted many times to get only A and count from this to the remainder that is 4 , so it would be
A B C D E F G F E D C B
Since I haven't learned modular arithmetic, I solved for the maximum number divisible by 6 that is below 1000. That number is 996. And since the pattern repeats D F F D B B, any number divisible by 6 is the goblet B. So counting from B, it should be goblet D.
A B C D E F G
1 2 3 4 5 6 7
14 13 12 11 10 9 8
15 16 17 18 19 20 21
Let's choose any goblet, I chose D and the pattern of D is as follows: 4+, 10-, 16+, 22-, 28+,...........n the numbers form an arithmetic sequence, while the sign is positive when n is odd and negative when n is even
for 1000th term:
4 + 6 ⋅ ( n − 1 ) = 1 0 0 0
6 ⋅ ( n − 1 ) = 9 9 6
n = 1 6 7
since n is an integer, D is already the gold goblet. We don't have to calculate the sign.
What if n is not an integer, what if the 1001st goblet is the golden one, which one would it be, how would we know whether it's C or E? That can be determined using the sign: n is odd so the sign is positive and E is the 1001st goblet.
You don't even need to use modular arithmetic. Just notice that you pattern in counting restarts every 12, and 12 divides 996, so when you have counted 996, you just restart at A. So 997 is A...1000 is D.
I just count to 1,000 which takes lesser than 5 minites if you are good at quick counting and get low human errors.
Just Kidding.I just count to 100 and it ended up in D.Repeat that 10x and it confirmes land in D.
Another way is to observe that counting 12 times will end up in B easily.So I took 1000/12 and the remainder would be 4.Count that from A and you end up in D.
Basic Java code to solve it:
public class Goblet{
//Since it's ABCDEFG (and then it goes back) FEDCB (and then it starts over again). So we can use % to get the module, thus the answer.
static int numberOfGoblets = 12;
public static void main(String[] args){
System.out.println(1000%numberOfGoblets);
}
}
Moderator note:
This problem does not need the assistance of computational aid. It would be much easier once you know the basics of modular arithmetic.
goblet A=25, B=50 C=75 D=100 thus with increment of every 25 we move to the next goblet hence goblet D is the 1000th. ie goblet 4.
Moderator note:
This solution has been marked incomplete because you failed to show why we move to the next goblet for every increment of 25.
I counted to 25 50 75 100 they fall on a b c d etc. You can mark complete
Log in to reply
1000 / 12 first ones of series. ( a b c d e f g f e d c b) after that it is reapeted again and again = 83.33333333333 take the friction mutiple it in 12 then it is 4 So the golden one is the fourth one (d)
to confusing for me and make it easier for the people seeing your work
For this problem you can use modular arithmetic .
The first 12 steps are A,B,C,D,E,F,G,F,E,D,C,B and then it repeats itself again. So, we just need to see how many sets of 12 steps there are, and then find the remainder number of steps.
Since 1 0 0 0 ≡ 4 ( m o d 1 2 ) , therefore you should pick the 4 t h goblet