Chord-Diameter Intersection
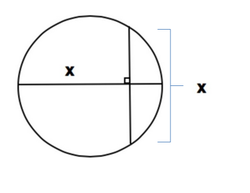If the circle above has a diameter of 1, and
x
can be written in the form
b
a
, where
a
and
b
are coprime integers. Find the value of
a
+
b
.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
What if we use the Chord-Chord theorem? Then it would be x(2-x)=x^2/4. From this it would follow that 5x^2/4=2x and x=8/5. Therefore the answer should be 13.
Log in to reply
Oh no! When I made the question I envisioned a circle of DIAMETER length 1, the unit circle is radius length 1. You sir are correct, and I thank you. I have updated the problem to reflect my original intentions, thanks again.
Log in to reply
No problem, just got confused a bit and tried to see how the solution worked. How do I get the points back for this problem though? :)
Log in to reply
@John Taylor – Haha I wish I could give them to you, you'll just have to solve one of my other problems instead! ;)
Log in to reply
@Garrett Clarke – So according to the chord theorem x (1-x)= x^2/4 and doing some algebra we get 4x-4x^2= x^2 which then equals -5x^2+ 4x=0 or 5x^2-4x= 0 so x= 0 and x= 4/5 so the answer is actually 9 not 13
Log in to reply
@Brandon Lopez – Yes the answer is 9 , originally I had stated that the circle was the unit circle, which led to the solution of 5 8 ⟹ 8 + 5 = 1 3 , but I've since changed the problem to make the circle have a diameter of 1 , as opposed to having a radius of 1 , which leads to the solution x = 5 4 ⟹ 4 + 5 = 9 .
This is immediate by Circles - Intersecting Chords . x ( 1 − x ) = ( 2 x ) 2 ⇒ x = 5 4 .
If we draw two extra lines, the solution becomes a little clearer.
These two lines create a triangle, and since the hypotenuse of our triangle is the diameter of a circle, it's a right triangle.
Our chord also meets our hypotenuse at a right angle, making it an altitude. As you can see, this altitude splits our right triangle into two more right triangles. Because of the Geometric Mean Theorem, if an altitude meets the hypotenuse, the two triangles that it creates are similar triangles, meaning that their sides are proportional to each other. Now all we have left to do is set up our proportion and solve for x.
2 x 1 − x = x 2 x
1 − x = 4 x
1 = 4 5 x
x = 5 4 ⟹ 4 + 5 = 9