A classical mechanics problem by Krishna Shankar

Classical Mechanics Level 3

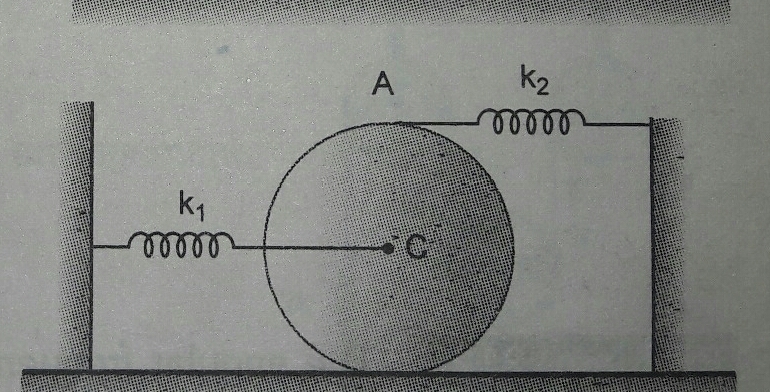
A solid cylinder of mass $m=1 \text{ kg}$ is kept in equilibrium on a horizontal surface.

Two unstretched springs of forces $k_1=10 \text{ Nm}^{-1}$ and $k_2=20 \text{ Nm}^{-1}$ are attached to the cylinder as shown in figure.
Find the period (in seconds, $s$ ) of small oscillations.

Assume that the cylinder rolls without sliding.

0.81\text{ s}

0.88\text{ s}

0.83\text{ s}

0.86\text{ s}

0.85\text{ s}

2 solutions

Steven Chase
Dec 14, 2016

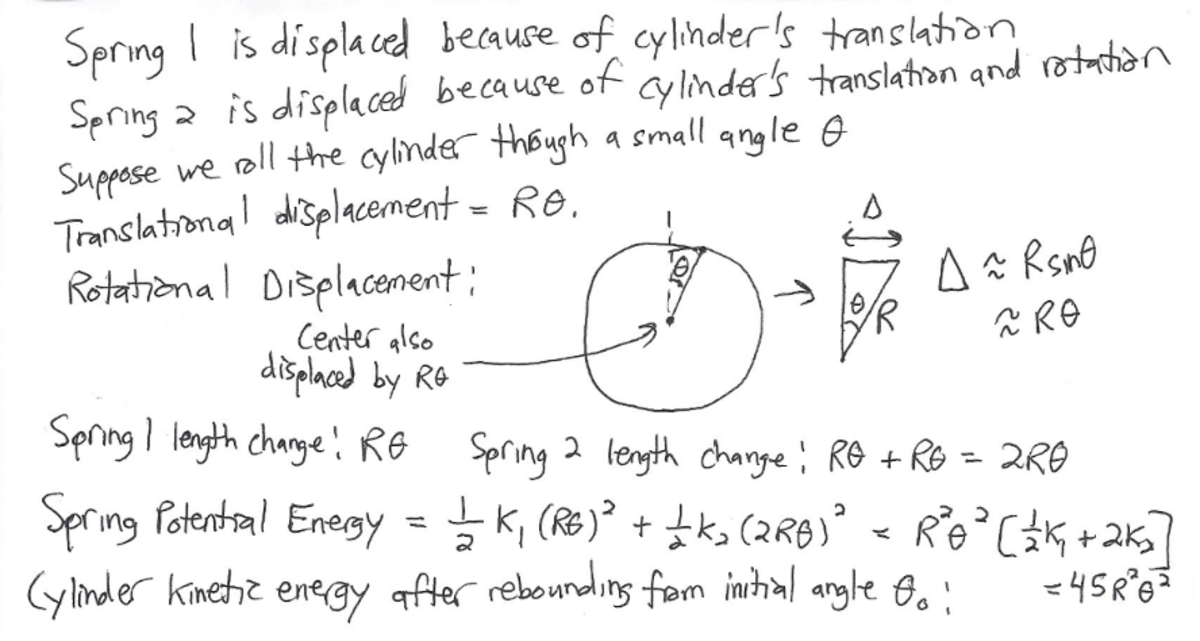
If the cylinder rolls then isn't there friction and thus energy lost?

Shaun Leong - 4 years, 3 months ago

If a cylinder rolls without slipping, there is no energy loss due to friction. So I think not. I find that to be counter-intuitive as well.

Steven Chase - 4 years, 3 months ago

We say work is done when the point of application of force undergoes displacement not the the body as whole, thus in case of pure rolling, the bottommost point is instantaneously at rest so we say friction foes no work when rolling is without slipping , hope it makes the point clear.

Harsh Shrivastava - 4 years, 3 months ago

instead of sin it would be arcsin() sir :)

A Former Brilliant Member - 4 years, 3 months ago

In which part?

Steven Chase - 4 years, 3 months ago

last step jusr before u get the ans.

A Former Brilliant Member - 4 years, 3 months ago

@A Former Brilliant Member – Oh, yes. "asin" is the same thing as "arcsin"

Steven Chase - 4 years, 3 months ago

@Steven Chase – sorry sir i saw that a just now :P

A Former Brilliant Member - 4 years, 3 months ago

Niraj Sawant
Mar 21, 2019

The two springs act in series hence, $k_{eff} = \dfrac {k_1 k_2}{k_1 + k_2} = \dfrac {2}{30}$

Time period, $T = π\sqrt {\dfrac {2}{30}} = 0.8111557 = \boxed {0.81s}$

A classical mechanics problem by Krishna Shankar

2 solutions

0 pending reports