Christmas Streak 45/88: Weird Quadrilateral, I Admit
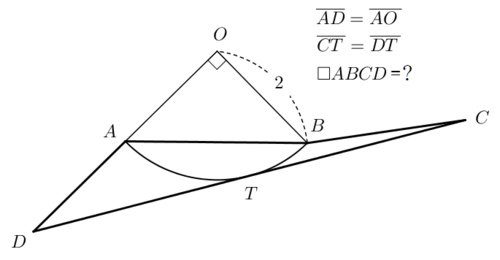
A is the midpoint of D O . T is the midpoint of C D , and is the point of contact of C D and quadrant circle O .
Find the area of □ A B C D to 4 decimal places.
This problem is a part of <Christmas Streak 2017> series .
The answer is 2.92820.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Do we need to find O H ?
Log in to reply
The length of O H is needed to figure out the area of △ B C O .
Log in to reply
Oh! I used the fact ∠ B O C = 6 π and O C = 4 to get the area of △ B C O .
N o t e t h a t Δ O D C a l t i t u d e O T − ( r a d i u s a t p o i n t o f t a n g e n t c y ) i s a l s o p e r p e n d i c u l a r b i s e c t o r o f B a s e D C . ∴ D e l t a O D C i s i s o s c e l e s , O C = O D = 4 . .
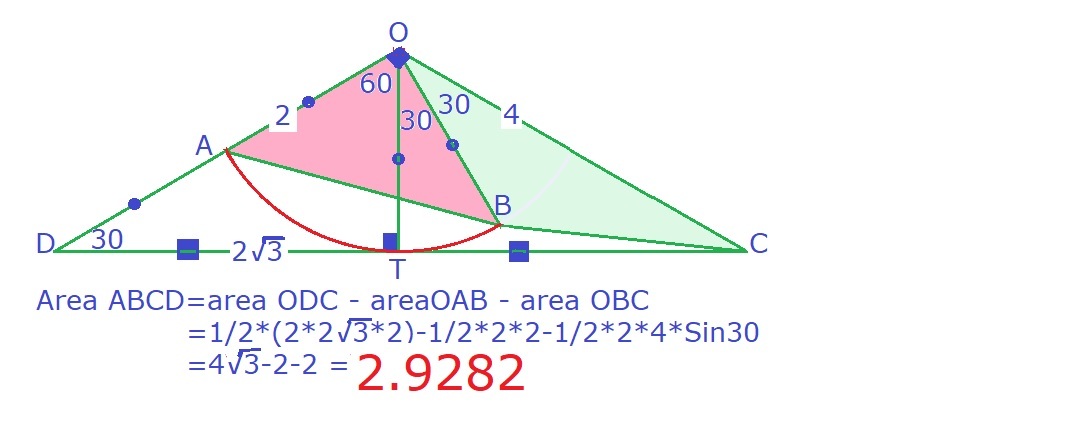
Again, take a look at this beautiful diagram.
Note that O T = 2 and O D = 4 .
Therefore ∠ C D H = 3 0 ∘ .
Since C D = 2 D T = 4 3 , we figure out that D H = 6 .
Then O H = 2 .
□ A B C D = △ O D C − △ A B O − △ B C O = 4 3 − 2 − 2 = 4 ( 3 − 1 ) ≈ 2 . 9 2 8 2 0 .