Christmas Streak 49/88: Diophantine #3

Relevant wiki: Quadratic Diophantine Equations - Solve by Factoring

$\sqrt{x^2+9x}=t \\ \\ x^2+9x=t^2 \\ \\ \left(x+\dfrac{9}{2}\right)^2-\dfrac{81}{4}=t^2 \\ \\ (2x-2t+9)(2x+2t+9)=81 \\ \\ \cases{2x-2t+9=1 \\\\ 2x+2t+9=81}~\text{or}~\cases{2x-2t+9=3 \\\\ 2x+2t+9=27}~\text{or}~\cases{2x-2t+9=9 \\\\ 2x+2t+9=9} \\\\ \cases{x=16 \\\\ t=20}~\text{or}~\cases{x=3 \\\\ t=6}~\text{or}~\cases{x=0 \\\\ t=0}$

Since $x$ needs to be maximized, the answer is $\boxed{16}.$

We need $x^2+9x=n^2$ for some integer $n$ .

$x^2+9x-n^2=0$

$x=\frac{-9\pm\sqrt{81+4n^2}}{2} \implies x=\frac{-9+\sqrt{81+4n^2}}{2}$ to maximize $x$ . Thus, $2x+9=\sqrt{81+4n^2}$ . Therefore, we can create a right triangle with sides $9$ , $2n$ , and $2x+9$ .

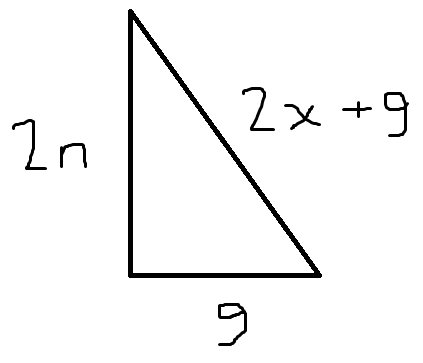
The Pythagorean triplet with length $9$ that maximizes the length of the hypotenuse (and thus $x$ ) is the $9-40-41$ right triangle (see below). This can be accomplished with $n = 20$ and $\boxed{x = 16}$ .

For primitive Pythagorean triplet $a-b-c$ , where $c$ is the hypotenuse, the three sides can be generated by choosing two positive coprime integers with different parity $r$ and $s$ with $r > s$ :

$a=r^2-s^2$

$b=2rs$

$c=r^2+s^2$

Choosing $r=5$ and $s=4$ , we get the $9-40-41$ triangle. There are no other perfect squares with a difference of $9$ (note that for any integer $a$ , $(a+1)^2-a^2>a^2-(a-1)^2 \implies 1>-1$ , so consecutive differences of perfect squares will get increasingly larger than $9$ after $25$ , and smaller values can be tested with trial and error). $9$ cannot be equal to $2rs$ since it is odd, and it cannot be $c$ since it is a leg of the triangle. $9$ can also be created from scaling up another primitive Pythagorean triplet, but the only such triangle can be created by scaling up a $3-4-5$ triangle to get a $9-12-15$ triangle. Therefore, we have found the largest value for the hypotenuse.

Relevant wiki: Quadratic Diophantine Equations - Solve by Bounding Values

The question is equivalent to ask find the biggest integer value of $x$ such that $x^2+9x$ is a perfect square. Since $x = 0$ gives us $x^2 + 9x = 0$ is a perfect square, we only need to consider positive $x$ only.

Obviously, $x^2+9x> x^2$ and $x^2+9x< x^2+10x+25=(x+5)^2$ . Hence, we can conclude that $x^2+9x$ is equal to $(x+k)^2\space\space(k=1,2,3,4)$ , because $x^2+9x$ is a perfect square between perfect squares $x^2$ and $(x+5)^2$ .

Try and error, we can get $x=3,16$ . Hence, the answer is $\large 16$ .

$\sqrt{x^2 + 9x} = y$ $x^2 + 9x = y^2$ Completing the square is usually a good idea! First, however, we multiply everything by four to avoid fractions. $(2x)^2 + 2\cdot 9(2x) + 9^2 = (2y)^2 + 9^2$ $(2x + 9)^2 - (2y)^2 = 9^2$ $(2x + 9 + 2y)(2x + 9 - 2y) = 9^2.$ The expressions in brackets must be integers. Obviously, the largest possible value of either expression is 81. To optimize $x$ , therefore, we write $81\cdot 1 = 9^2$ : $\begin{cases} 2x + 9 + 2y = 81 \\ 2x + 9 - 2y = 1 \end{cases}$ Add these to find $4x + 18 = 82 \ \ \ \therefore\ \ \ x = \boxed{16}.$ Indeed, $\sqrt{16^2 + 9\cdot 16} = \sqrt{16\cdot (16+9)} = \sqrt{16}\sqrt{25} = 4\cdot 5 = 20.$

Here's a solution for the more visually-minded, like me. 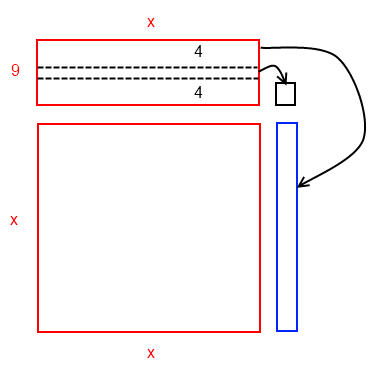On the bottom is an x by x square, and above it is a 9 by x rectangle. You want to break up the rectangle and add the pieces to the square to make another square. You slice the rectangle into three pieces, two that are 4 by x and one that is 1 by x, and move one of the 4 by x pieces to the side of the square, as shown. Then the remaining 1 by x piece will have to make up the missing smaller square. Since that square is, we know, 4 by 4, then it must have 16 unit squares in it. It was a one by x rectangle, so x must have been 16.

I just plugged it into excel, hoping the answer was small. The only values that have integer results were 3 and 16.

x²+9x=(x+a)²; (x+a) > x because 9x is positive and a is positive integer x²+9x=x²+2ax+a² (9-2a)x=a² x=a²/(9-2a) for largest x (9-2a) must be positive, a is integer 0<a<=4 for all values of a (a,x); (1, 1/7), (2, 4/5), (3, 3), (4, 16) max possible value of x is 16

I enjoy seeing the approaches everyone uses. Here I chose the brute-force approach, since all possible solutions must be integers, and likely small integers at that. A quick Excel spreadsheet covers all integers from -64 to 63 (no particular reason to cut off there, though). Solutions to the problem as stated are -25, -12, -9, 0, 3, and 16. Because the problem asks for the largest rather than the most positive, it seems the correct answer should be -25.

I have a solution with no trial and error which I haven't seen yet: Rewrite x^2+9x as x(x+9) For this to be a perfect square, both x and x+9 must be perfect squares Since we know the difference between the squares goes up as the odd numbers (1,4,9... difference is 3,5,7 etc), the max value of x is when x+9 is the next square, giving us 16.

I paraphrased this question as "what does $9x$ need to be so that $x^2+9x$ is a square".

Every square larger than $x^2$ is of the form $(x+n)^2$ , so

$x^2+9=(x+n)^2\\\\ x^2+9x=x^2+2nx+n^2\\\\ 9x=2nx+n^2\\\\ 9x-2nx=n^2\\\\ (9-2n)x=n^2\\\\ n^2>0\implies(9-2n)x>0\implies9-2n>0\implies2n<9\implies n\in\{1,2,3,4\}$

From this we get

$7x=1\\\\ 5x=4\\\\ 3x=9\\\\ x=16$

And so the only integer solutions are 3 and 16.

Note that we can factor $x^2+9x$ as $x(x+9)$ . Suppose $x^2+9x$ is a perfect square. Now suppose some prime $p$ divides $x$ . Then $p|(x+9) \implies p|(x+9)-x = 9 \implies p=3$ . Therefore unless $p=3$ , we must have that $p^2|x$ , and further that $x$ has an even number of factors of $p$ . This means that $x = 3n^2$ or $x=n^2$ for some $n$ . In the case $x=3n^2$ , we have that $x^2+9x = 9n^4+27n^2 = 9n^2(n^2+3)$

This implies that $n^2+3$ is a perfect square, which we know only happens for $n=1$ . Thus $x = 3$ is one possible solution.

In the case $x = n^2$ , we have $x^2+9x = n^4+9n^2 = n^2(n^2+9)$ . This means $n^2+9$ is a perfect square, and the largest $n$ for which that is true will be when $n^2+9 = (n+1)^2 \implies n = 4$ . Thus $x = \boxed{16}$ is the largest possible $x$ .

Simplified to (square root x).(square root X+9)

Therefore X and X+9 must be whole numbers And since the whole numbers grow in sequence exponentially, then finding the two whole numbers whose difference equals 9 is easy. sr16.sr(16+9)= sr4.5 =20 Unfortunately this approach didn't get neither number 3 or 0 possibility.

Let $n=\sqrt{x^2+9x}$ . $x,n$ are integers.

Thus $n^2=x^2+9x$ .

Let $x=n-k$ , thus $k$ is also an integer.

$x^2=(n-k)^2=n^2-2kn+k^2$

By rearranging the above: $n^2=x^2+(2kn-k^2)$

So $9x=2kn-k^2$

Substituting for $n$ : $9x=2k(x+k)-k^2$

In terms of $x$ : $x=\frac{k^2}{9-2k} - (1)$

Since the numerator is of higher order, maximising $k$ maximises $x$ .

It can be seen from the denominator that for the constraint $x≥0$ , $k≤\frac{9}{2}$ .

Maximum integer $k$ under this constraint is $4$ . From $(1)$ , this yields $x=16$ , which happens to be an integer.

I worked it out in my head and found 3 was a solution. Like another respondent, I tried it in Excel, but with both positive and negative x, up to +1000 and down to -1000. The ONLY solutions are x=16, 3, 0, -9, -12 and -25. It is clear these are the only ones, because as x tends to +infinity, sqrt(xsq+9x) tends to x + 4.5, and x tends to -infinity, sqrt(xsq+9x) tends to x - 4.5, as would be predicted by a series expansion. But what is interesting is the VALUES of sqrt(xsq+9x) corresponding to these solutions. These are 20, 6, 0, 0, 6, 20. There is no obvious symmetry to the sequence x=16, 3, 0, -9, -12 and -25, in contrast. And 20, 6, 0, 0, 6, 20 can be written 5 * 4, 3 * 2, 1 * 0 etc.

General solution for any $\sqrt{ x^2 + (2n + 1) x }$ is to observe the fact that $n^2 = \sum_{k = 1}^n { 2k - 1}$ and $\sqrt{ x^2 + (2n + 1) x } = \sqrt{ x } \sqrt{x + (2n + 1)}$

in other words, the question requires both $x$ and $x + (2n + 1)$ to be square

or in other words both $1 + 3 + 5 + ... + (2\sqrt{x} - 1)$ and $1 + 3 + 5 + .... + (2\sqrt{x} - 1) + ( 2n + 1)$ to be square

the largest point this is achieved is at $x = n^2$ , exceeding that would prevent one multiple or the other being a square number, in this case $n = 4$ , therefore the solution is 16!

If sqrt(x^2 + 9x) is an integer, then x^2 +9x is the square of an integer, which we designate as x+n. So, x^2 + 9x = (x+n)^2. Solving, we have x = n^2/(9-2n). We want the largest possible value for x and we want x to be an integer. If n=4, then 9-2n=1>0 and x=16.

OK how about this:

1. We want x(x+9) to be a large square number.

2. Note that the square number needs paired up prime factors in order to have an integer root.

3. In my usual way of doing solutions, I note that the difference between squares is in the sequence of odd numbers, i.e. ...

4. How about 16 and 25, which have a difference of 9 and luckily happen to be square numbers themselves . Therefore their multiple also has an integer root.

5. Therefore 16 is a pretty good answer.

QUESTION:

Is this method alone sufficient to prove that there are no higher numbers that fit the bill?

Let $\sqrt{x^2+9x}=z$ . Then we solve the equation $x^2+9x-z^2=0$ in $x$ , and, in order for $x$ to be the largest possible integer value, we take $x=\dfrac{-9+\sqrt{4z^2+81}}2$ . So $x$ is an integer only if the expression $4z^2+81$ is a perfect square, which means that it is necessary to be of the form $4z^2+2\cdot 2z\cdot p+p^2$ , i.e. $81=4zp+p^2=p(4z+p)$ . Since $81=3^4$ , possible divisors are $p=1,3,9,27,81$ . If $p=1$ , then $4z+1=81$ , and we find $z=20$ . If $p=3$ , then $4z+3=27$ , and $z=6$ . If $p=9$ , then $4z+9=9$ , and $z=0$ . If $p=27$ , then $4z+27=3$ , and $z=-6$ . Finally, if $p=81$ , then $4z+81=1$ , and $z=-20$ . So, the largest possible integer value of $x$ is obtained for $z=20$ , i.e. $x=16$ .

Well, pass the calculating part to the computer, with just a simple program, I got 3 results: 0, 3 and 16.

This can be generalized.

Let $a$ be an odd prime.

Find largest positive integer $x$ such that $x^2 + a^2 x = j^2$ , where $j$ is an positive integer.

$x^2 + a^2 x = j^2 \implies (2x + a^2)^2 - a^4 = (2j)^2 \implies (2x + a^2)^2 - (2j)^2 = a^4 \implies (2x - 2j + a^2) (2x + 2j + a^2) = a^4$

$2x + 2j = a^4 - a^2$

$2x - 2j = 1 - a^2$

$\implies x = (\dfrac{a^2 - 1}{2})^2 = k^2 \in \mathbb{N}$ and $j = \dfrac{(a - 1)(a^3 + a^2 + 1)}{4} = m * l \in \mathbb{N}$

$2x + 2j = a^3 - a^2$

$2x - 2j = a - a^2$

$\implies x = a (\dfrac{a - 1}{2})^2 = 2 h n^2 \in \mathbb{N}$ and $j = a (\dfrac{a^2 - 1}{2})^2 = 2 q s^2 \in \mathbb{N}$

$2x + 2j = 0$

$2x - 2j = 0$

$\implies x = j = 0$ clearly $x = 0 \neq x_{max}.$

For $a > 1$

$(a^2 - 1)^2 - a(a - 1)^2 = (a - 1)^2 (a + 1)^2 - a (a - 1) = (a - 1)^2 (a^2 + a + 1) > 0 \implies (a^2 - 1)^2 > a(a - 1)^2 \implies$ $(\dfrac{a^2 - 1}{2})^2 > a (\dfrac{a - 1}{2})^2$

$\therefore x = x_{max} = (\dfrac{a^2 - 1}{2})^2$

For instance using $a = 7919 \implies x_{max} = \boxed{983153583878400}$ .

I tried to make $x^2+9x$ a perfect square.

Think of it as

$(x+1)^2=x^2+2x+1=x^2+9x$ (then $7x=1$ , $x=\frac{1}{7}$ is not an integer)

or

$(x+3)^2=x^2+6x+9=x^2+9x$ (so $3x=9$ , $x=3$ ).

Then the largest possible integer for $x$ becomes $16$ , since

$(x+4)^2=x^2+8x+16=x^2+9x$

that gives us $x=16$ .

And we can't go any further, because the coefficient of the linear term can't exceed $9$ , or it will not able to be made a perfect square.

$\sqrt{x^2+9x}=c$

$\sqrt{x(x+9)}=c$ Therfore, x and (x+9) must both be perfect squares. The only perfect squares that have a difference of 9 are 25 and 16. Therefore x=3

This solution is pretty roundabout, but it's different; letting $y=\sqrt{x^2+9x}$ and $a=y-x$ , we have $\begin{aligned} (y-x)(y+x)&=9x\\ a(a+2x)&=9x\\ \Longrightarrow x&=\dfrac{a^2}{9-2a}.\tag{1} \end{aligned}$ Note that if $y=x$ , we obtain only one solution of $y=x=0$ . Substituting $x=1$ yields $y=\sqrt{10}>1$ , which means that $y>x\;\; \forall \;\; x\geq 1$ . Hence, $a>0$ . Now, to maximise $x$ , we must minimise $9-2a$ and maximise $a^2$ (from $(1)$ ), both of which can be achieved by increasing $a$ . Thus, we choose the largest integer $a$ (since $a\in \mathbb{Z}^+$ ) such that $9-2a>0$ (otherwise $x<0$ ). This is clearly $4$ , since $9-2\times 5=-1<0$ . This means that the maximum value of $x$ over all positive, integral $a$ is $4^2/(9-2\times 4)=16$ , which is itself an integer, meaning we are done.

Hence, the largest integer $x$ such that $\sqrt{x^2+9x}$ is an integer is $\boxed{16}$ .

sqrt(x^2+9x)=sqrt(x)*sqrt(x+9), if x=16 then 16+9=25 is also a square number

import math

def isInteger(num):
    res = math.sqrt(pow(num,2) + 9*num)
    if res % 1 == 0:
        return True
    else:
        return False

for i in range(0,1000):
    q = isInteger(i)
    if q:
        print(str(i) + ": " + str(q))(q))

If we let y equal the expression, we can write it as: $x^{ 2 }+9x = { y }^{ 2 }$

Now what do you add to a square number to form another square number? A triangular number!

We can deduce 9x is the (x+1)th triangular number, because it's the amount that's wrapped around the initial square.

So now we can form the expression: $\frac { { n }^{ 2 }+n }{ 2 } = 9n$

which simplifies to: ${ n }^{ 2 }-17n = 0$

The solutions are 0 and 17. Since we want the bigger value, we'll roll with 17.

So, x + 1 = 17

$\boxed{x = 16}$

Let r = gcd(x,y), so that x = ar, y = br with (a,b) = 1. Substituting, (a^2)(r^2) + 9(at) = (b^2)(r^2). Dividing by r, ra^2 + 9a =rb^2. Since (a,b) =1, a|r. Let r = ac. Then ca^3 + 9a = acb^2. Dividing by a, ca^2 + 9 =cb^2. Hence, c = 1,3, or 9. If c = 1, a^2 + 9 = b^2, b^2 - a^2 =9, and (b - a)(b + a) = 9, so b -a =1, b+ a = 9, 2b= 10, b =5, a =4, r=ca = 4, x= ar = 16.Repeating the calculation for c = 3 or c = 9 results in smaller values for x. Ed Gray